人教A版数学必修三1-3算法案例（复习） 5页

算法初步 复习课 一、教学目标 1、知识与技能 （1）明确算法的含义，熟悉算法的三种基本结构：顺序、条件和循环，以及基本的算法语句。 （2）能熟练运用辗转相除法与更相减损术、秦九韶算法、排序、进位制等典型的算法知识解决同类 问题。 2、过程与方法 在复习旧知识的过程中把知识系统化，通过模仿、操作、探索，经历设计程序框图表达解决问题的过 程。在具体问题的解决过程中进一步理解程序框图的三种基本逻辑结构：顺序、条件分支、循环。 3、情态与价值观 算法内容反映了时代的特点，同时也是中国数学课程内容的新特色。中国古代数学以算法为主要特征， 取得了举世公认的伟大成就。现代信息技术的发展使算法重新焕发了前所未有的生机和活力，算法进入中 学数学课程，既反映了时代的要求，也是中国古代数学思想在一个新的层次上的复兴，也就成为了中国数 学课程的一个新的特色。 二、教学重难点 重点：算法的基本知识与算法对应的程序框图的设计 难点：与算法对应的程序框图的设计及算法程序的编写 三、学法与教学用具 学法：利用实例让学生体会基本的算法思想，提高逻辑思维能力，对比信息技术课程中的程序语言的 学习和程序设计，了解数学算法与信息技术上的区别。通过案例的运用，引导学生体会算法的核心是一般 意义上的解决问题策略的具体化。面临一个问题时，在分析、思考后获得了解决它的基本思路（解题策略）， 将这种思路具体化、条理化，用适当的方式表达出来（画出程序框图，转化为程序语句）。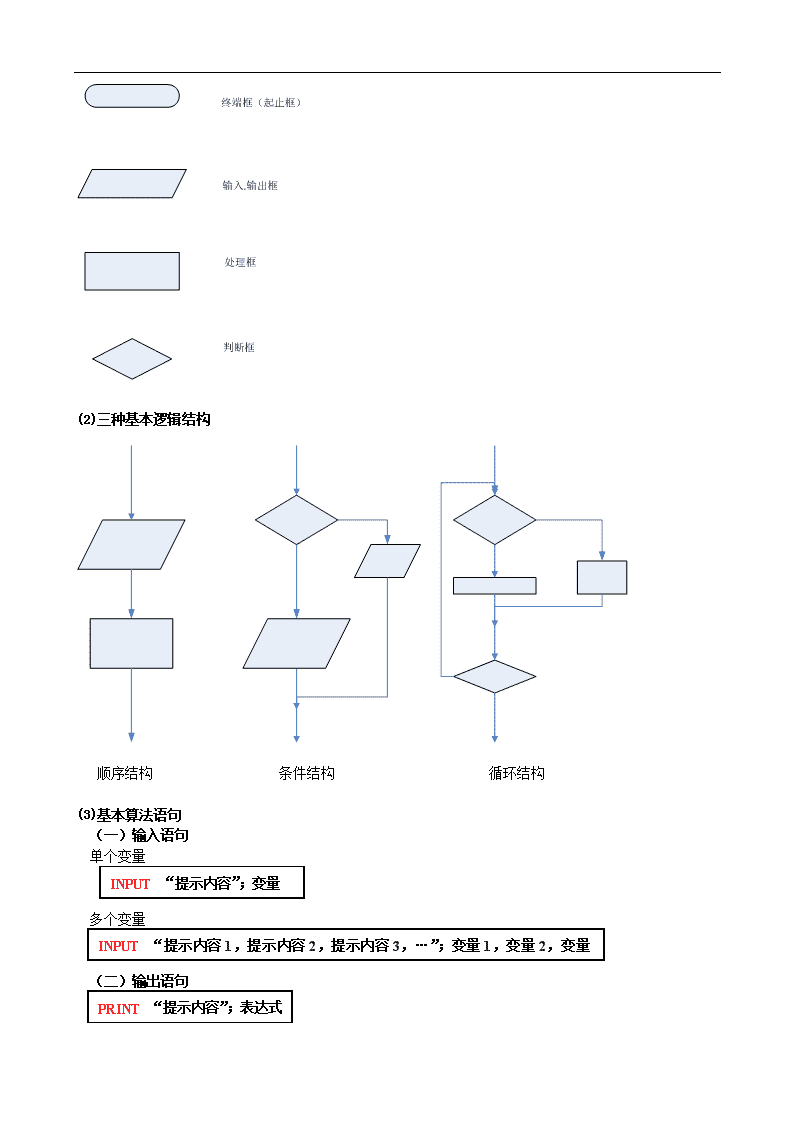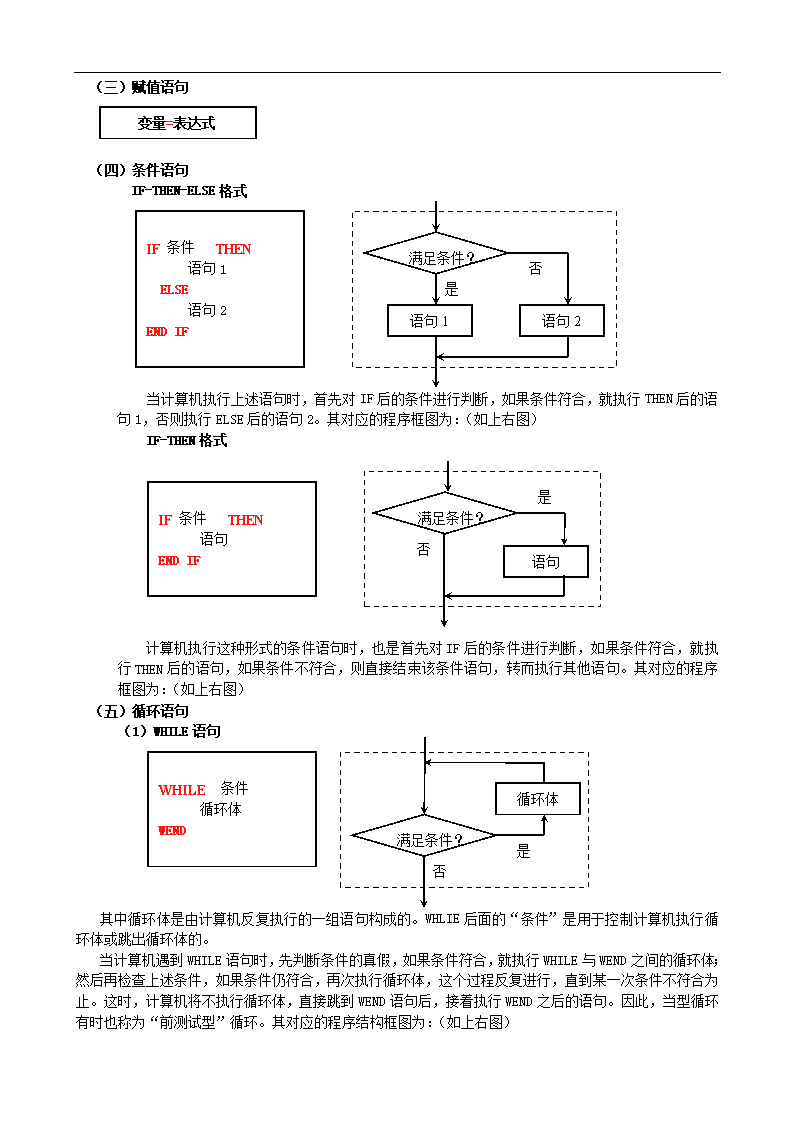 教学用具：电脑，计算器，图形计算器 四、教学设计 （一）、本章的知识结构 （二）、知识梳理 (1)四种基本的程序框 (2)三种基本逻辑结构 顺序结构 条件结构 循环结构 (3)基本算法语句 （一）输入语句 单个变量 多个变量 （二）输出语句 INPUT “提示内容”；变量 INPUT “提示内容 1，提示内容 2，提示内容 3，…”；变量 1，变量 2，变量 3，… PRINT “提示内容”；表达式 （三）赋值语句 （四）条件语句 IF-THEN-ELSE 格式 当计算机执行上述语句时，首先对 IF 后的条件进行判断，如果条件符合，就执行 THEN 后的语 句 1，否则执行 ELSE 后的语句 2。其对应的程序框图为：（如上右图） IF-THEN 格式 计算机执行这种形式的条件语句时，也是首先对 IF 后的条件进行判断，如果条件符合，就执 行 THEN 后的语句，如果条件不符合，则直接结束该条件语句，转而执行其他语句。其对应的程序 框图为：（如上右图） （五）循环语句 （1）WHILE 语句 其中循环体是由计算机反复执行的一组语句构成的。WHLIE 后面的“条件”是用于控制计算机执行循 环体或跳出循环体的。 当计算机遇到 WHILE 语句时，先判断条件的真假，如果条件符合，就执行 WHILE 与 WEND 之间的循环体； 然后再检查上述条件，如果条件仍符合，再次执行循环体，这个过程反复进行，直到某一次条件不符合为 止。这时，计算机将不执行循环体，直接跳到 WEND 语句后，接着执行 WEND 之后的语句。因此，当型循环 有时也称为“前测试型”循环。其对应的程序结构框图为：（如上右图） IF 条件 THEN 语句 1 ELSE 语句 2 END IF 满足条件？ 语句 1 语句 2 是 否 IF 条件 THEN 语句 END IF 满足条件？ 语句 是 否 WHILE 条件 循环体 WEND 满足条件？ 循环体 是 否 变量=表达式 （2）UNTIL 语句 其对应的程序结构框图为：（如上右图） (4)算法案例 案例 1 辗转相除法与更相减损术 案例 2 秦九韶算法 案例 3 排序法：直接插入排序法与冒泡排序法 案例 4 进位制 （三）、典型例题 例 1 写一个算法程序,计算 1+2+3+…+n 的值(要求可以输入任意大于 1 的正自然数) 解：INPUT “n=”;n i=1 sum=0 WHILE i<=n sum=sum+i i=i+1 WEND PRINT sum END 思考：在上述程序语句中我们使用了 WHILE 格式的循环语句，能不能使用 UNTIL 循环？ 例 2 设计一个程序框图对数字 3,1,6,9,8 进行排序(利用冒泡排序法) DO 循环体 LOOP UNTIL 条件 满足条件？ 循环体 是 否 思考：上述程序框图中哪些是顺序结构？哪些是条件结构？哪些是循环结构？ 例 3 把十进制数 53 转化为二进制数. 解：53＝1×25＋1×24＋0×23＋1×22＋0×21＋1×20 ＝110101（2） 例 4 利用辗转相除法求 3869 与 6497 的最大公约数与最小公倍数。 解：6497＝3869×1＋2628 3869＝2628×1＋1241 2628＝1241*2＋146 1241＝146×8＋73 146＝73×2＋0 所以 3869 与 6497 的最大公约数为 73 最小公倍数为 3869×6497/73＝344341 思考：上述计算方法能否设计为程序框图？ 练习:P40 A(3) (4) （五）、评价设计 作业：P40 A（5）(6)