江苏省泰州中学2020届高三下学期第五次模拟考试数学试题 Word版含解析 27页

- 1 - 2019—2020 学年江苏省泰州中学高三年级第五次模拟考试 数学 I 卷 一、填空题 1. 已知集合  0A x x ，  1,0,1,2B   ，则 A B 等于 ． 【答案】 1,2 【解析】 试题分析：      | 0 1,0,1,2 1,2A B x x      考点：集合运算 【方法点睛】 1.用描述法表示集合，首先要弄清集合中代表元素的含义，再看元素的限制条件，明确集合 类型，是数集、点集还是其他的集合． 2．求集合的交、并、补时，一般先化简集合，再由交、并、补的定义求解． 3．在进行集合的运算时要尽可能地借助 Venn 图和数轴使抽象问题直观化．一般地，集合元 素离散时用 Venn 图表示；集合元素连续时用数轴表示，用数轴表示时要注意端点值的取舍． 2. 设i 是虚数单位，复数 z 满足 (3 4 ) 4 3i z i   ，则复数 z 的虚部为_____． 【答案】 1 【解析】 【分析】 利用复数的除法运算求得 z ，由此求得 z 的虚部. 【详解】依题意       4 3 3 44 3 25 3 4 3 4 3 4 25 i ii iz ii i i          ，所以 z 的虚部为 1 . 故答案为： 1 【点睛】本小题主要考查复数的除法运算，考查复数虚部的概念，属于基础题. 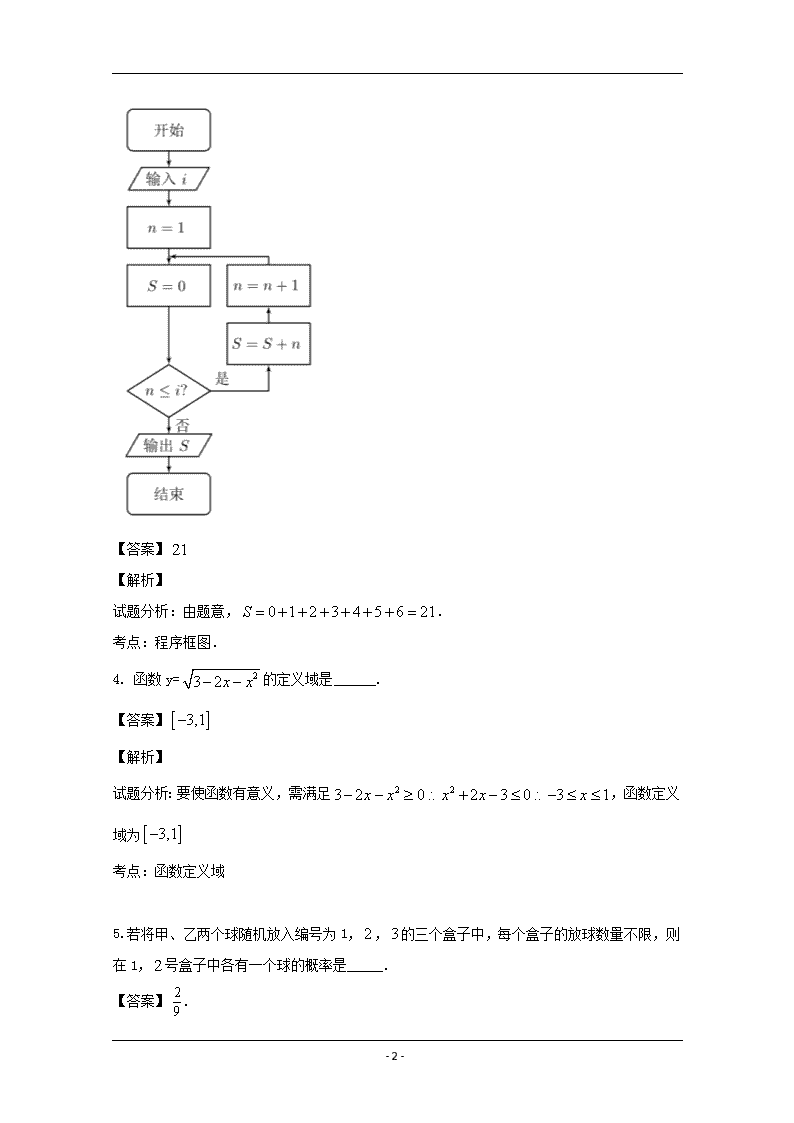3. 执行下图的程序框图，如果输入 6i  ，则输出的 S 值为 ． - 2 - 【答案】 21 【解析】 试题分析：由题意， 0 1 2 3 4 5 6 21S         ． 考点：程序框图． 4. 函数 y= 23 2x x  的定义域是 . 【答案】 3,1 【解析】 试题分析：要使函数有意义，需满足 2 23 2 0 2 3 0 3 1x x x x x          ，函数定义 域为 3,1 考点：函数定义域 5. 若将甲、乙两个球随机放入编号为 1， 2 ， 3 的三个盒子中，每个盒子的放球数量不限， 则在 1， 2 号盒子中各有一个球的概率是 ． 【答案】 2 9 . - 3 - 【解析】 试题分析：将甲、乙两个球随机放入编号为1，2 ，3 的三个盒子中，共有3 3=9 种方法，其 中在1， 2 号盒子中各有一个球有 2 1=2 种方法，因此所求概率是 2 .9 考点：古典概型概率 6. 若 x ， y 满足不等式组 1 1 0 1 x y x x y         ，则3 2x y 的最大值为______. 【答案】3 【解析】 【分析】 画出不等式组表示的平面区域，数形结合即可求得目标函数的最值. 【详解】画出不等式组表示的平面区域如下图所示： 目标函数 3 2z x y  ，即 3 2 2 zy x   与直线 3 2y x  平行. 数形结合可知，当且仅当目标函数过点  1,0A 时，取得最大值. 故 3maxz  . 故答案为：3 . 【点睛】本题考查简单线性规划问题的处理，属基础题. 7. 已知两条直线 m ， n ，两个平面 ，  ，给出四个命题： ①若 //m n ， m  ，则 n  ②若 / /  ， m  ， n  ，则 //m n ③若 / /m  ， m  ，则  ④若  ， / /m  ，则 m  - 4 - 其中正确命题的序号是_____． 【答案】①③ 【解析】 【分析】 根据直线与直线，直线与平面，平面与平面的位置关系逐一判断即可. 【详解】对①，由线面垂直的性质以及判定定理可知，①正确； 对②，若 / /  ， m  ， n  ，则 ,m n 异面或者平行，②错误； 对③，由面面垂直的判定定理可知，③正确； 对④，若  ， / /m  ，则 m 可能在  内或与  平行或与  相交，④错误； 故答案为：①③ 【点睛】本题主要考查了判断直线与直线，直线与平面，平面与平面的位置关系，属于中档 题. 8. 等差数列{ }na 的公差为 2， nS 是数列{ }na 的前 n 项的和，若 20 40S  ，则 1 3 5 7 19a a a a a     _________． 【答案】10 【解析】 【分析】 利用等差数列奇数项的和与偶数项的和的关系即可求解. 【详解】等差数列{ }na 的公差为 2， 20 40S  ， 则 20 1 2 3 19 20S a a a a a      1 3 5 17 19 2 4 18 20a a a a a a a a a           1 3 5 17 19 1 3 17 19a a a a a a d a d a d a d                1 3 5 17 192 10 40a a a a a d       ， 解得 1 3 5 7 19 10a a a a a     . 故答案为：10 【点睛】本题考查了等差数列的奇数项的和与偶数项的和，掌握等差数列的性质是关键，属 - 5 - 于基础题. 9. 已知双曲线 2 2 2 14 x y b   的右焦点与抛物线 2 12y x 的焦点重合，则该双曲线的渐近线方程 为______. 【答案】 5 2y x  【解析】 【分析】 求出抛物线的焦点坐标，根据题意可以知道双曲线的右焦点坐标，结合双曲线标准方程中 , ,a b c 之间的关系求出b 的值，最后利用双曲线的渐近线方程进行求解即可. 【详解】因为抛物线 2 12y x 的焦点坐标为 (3,0) ，所以双曲线 2 2 2 14 x y b   的右焦点也是 (3,0) ，即 3c  ，而 2 2 2 29 4 5c a b b b       ，所以该双曲线的渐近线方程为 5 2y x  . 故答案为： 5 2y x  【点睛】本题考查了求双曲线的渐近线方程，考查了抛物线的焦点，考查了数学运算能力. 10. 在平面直角坐标系 xOy 中，直线 1 : 4 0l kx y   与直线 2 : 3 0l x ky   相交于点 P ， 则当实数 k 变化时，点 P 到直线 4 3 10 0x y   的距离的最大值为__________． 【答案】 9 2 【解析】 【分析】 判断出 P 点的轨迹，然后根据直线和圆的位置关系，求得 P 到直线 4 3 10 0x y   的距离的 最大值. 【详解】设直线 1l 与 y 轴交于  0,4A ，直线 2l 与 x 轴交于  3,0B ， 2 23 4 5AB    . - 6 - 当 0k  时，直线 1l 为 4y  ，直线 2l 为 3x  ，所以两条直线的交点为  1 3,4P . 当 0k  时，两条直线的斜率分别为 k 、 1 k  ，斜率乘积为 1 ，故 1 2l l ，所以 P 点的轨迹是 以 AB 为直径的圆（除 ,A B 两点外）. 设以 AB 为直径的圆的圆心为 3 ,22C      ，半径 5 2 2 ABr   ，圆的方程为   2 2 23 522 2x y             .点  1 3,4P 满足圆的方程. 综上所述，点 P 点的轨迹是以 AB 为直径的圆（除 ,A B 两点外）. 圆心C 到直线 4 3 10 0x y   的距离为  22 34 3 2 102 2 4 3 d         . 所以点 P 到直线 4 3 10 0x y   的距离的最大值为 5 92 2 2d r    . 故答案为： 9 2 . 【点睛】本题主要考查直线和直线的位置关系，考查直线和圆的位置关系，属于中档题. 11. 已知点 P 在 ABC 内，且满足 1 1 3 4AP AB AC    ，设 PBC 、 PCAV 、 PAB△ 的面 积依次为 1S 、 2S 、 3S ，则 1 2 3: :S S S  ______． 【答案】5:4:3 【解析】 【详解】因为    1 1 1 1 3 4 3 4AP AB AC PB PA PC PA            ， 所以 5 4 3 0PA PB PC      ，所以 1 2 3: : 5: 4:3S S S  ． 12. 已知函数   24 , 0, { 3 , 0, x x x f x xx     若函数     3g x f x x b   有三个零点，则实数b 的 取值范围为__________． 【答案】 1( , 6) ( ,0]4     【解析】 - 7 - 【分析】 求 出 函 数  f x 的 解 析 式 ， 分 别 画 出 函 数  f x 与 3y x b  的 图 象 ， 将 函 数     3g x f x x b   有三个零点转化为函数  f x 与 3y x b  的图象的交点有三个求解 即可 【 详 解 】 3y x b  与 3 ( 0)y xx    相 切 时 6b   （ 正 舍 ）， 3y x b  与  24 0 4y x x x    相切时 1 4b   ， 3y x b  与 2 4 ( 4)y x x x   不相切.由图可知 实数b 的取值范围为 , 6   1 ,04     . 故答案为  1, 6 ,04        . 【点睛】已知函数有零点求参数取值范围常用的方法和思路 (1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； (2)分离参数法：先将参数分离，转化成求函数值域问题加以解决； (3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结 - 8 - 合求解． 13. 已知函数 ( ) sin(2 )6f x x   ，若方程 3( ) 5f x  的解为 1 2 1 2(, 0 )x x x x    ， 1 2sin( )x x  ____________． 【答案】 4 5  【解析】 【分析】 根据 1 22 26 6x x      ，可得 2 1 2 3x x  ，所以 1 2 1sin( cos(2 )6)x x x     ，再根据 角的范围和同角公式可得结果. 【详解】依题意可知， 1 2 3sin(2 ) sin(2 )6 6 5x x     ， 因为 1 20 x x    ，所以 1 2 112 26 6 6 6x x         ， 所以 1 22 26 6x x      ，所以 1 2 2 3x x   ，所以 2 1 2 3x x  ， 所以 1 2 1 2sin( ) sin(2 )3x x x    1sin(2 )6 2x     1cos(2 )6x    ， 因为 2 1 2 3x x  1x ，所以 10 3x   ，所以 12 ( , )6 6 2x      ， 所以 2 2 1 1 3 4cos(2 ) 1 sin (2 ) 1 ( )6 6 5 5x x        ， 所以 1 2 4sin( ) 5x x   . 故答案为： 4 5  . 【点睛】本题考查了同角公式和诱导公式，属于基础题. 14. 已知 1x ， 2x 是函数   2 ln 2f x x m x x   ，m R 的两个极值点，若 1 2x x ，则  1 2 f x x 的取值范围为______． 【答案】 3 ln 2,02      【解析】 【分析】 - 9 - 先由题得所以 1 2 1 21, 2 mx x x x    ， 1 10 2x  .化简得  1 2 f x x = 1 1 1 1 11 ) 2 ln 1x x x x     （ ， 再构造函数 1 )x x g( )=（ 1 1 12 ln (0 )1 2x x xx    ，利用导数求函数的值域即得解. 【详解】由题得函数的定义域为 (0, ) ， 21( ) 2 2 (2 2 )mf x x x x mx x        ， 所以 1 2,x x 是方程 22 2 0x x m   的两个实数根， 所以 1 2 1 21, 2 mx x x x    ， 因为 1 2x x ， 1 > 0x ， 所以 1 1 20 2 1x x x    ， 所以 1 10 2x  . 所以   2 2 1 1 1 1 1 1 2 1 2 2 2 ln 2 ( 1) 2 ln 1=f x x m x x x x x x x x x      = 1 1 1 1 11 ) 2 ln 1x x x x     （ 记 1 1 11 ) 2 ln (0 )1 2x x x x xx      g( )=（ ， 所以 2 2 2 1 1( ) 1 2ln 2 ln( )( 1) ( 1)g x x exx x          由 10 2x  2 20 1, ln( ) 04 eex ex      ， 所以 ( ) 0, ( )g x g x   在 1(0 )2 ， 单调递减， 又由洛必达法则得当 0x  时， 2 1 lnln 01 1 x xx x x x x       ，即 0 0 lim( ln ) 0, lim ( ) 0x x x x g x     1 1 1 3( ) ln 2 ln 22 2 2 2g       ， 所以函数 g(x)的值域为 3 ln 2,02      . - 10 - 即  1 2 f x x 的取值范围为 3 ln 2,02      . 故答案为： 3 ln 2,02      【点睛】本题主要考查利用导数研究函数的极值和取值范围，意在考查学生对这些知识的理 解掌握水平和分析推理能力. 二、解答题 15. ABC 的内角 A ，B ，C 所对的边分别为 a ，b ，c .已知 cos cos ( )cosb A c B c a B   . （1）求 B 的大小； （2）若 D 在 BC 边上， 2 2BD DC  ， ABC 的面积为3 3 ，求 sin CAD . 【答案】（1） 3B  （2） 13 13 【解析】 【分析】 （1）利用正弦定理化简已知条件，然后利用两角和的正弦公式、诱导公式进行恒等变换，由 此求得 cos B 的值，进而求得 B 的大小. （2）利用三角形 ABC 的面积求得 c ，由余弦定理求得 AD ，利用勾股定理证得 AD BD ， 由此求得 AC 进而求得sin CAD 的值. 【详解】（1）因为 cos cos ( )cosb A c B c a B   ， 所以sin cos sin cos (sin sin )cosB A C B C A B   ， 所以sin cos sin cos 2sin cosB A A B C B  ， 即sin( ) 2sin cosA B C B  ， 因为在 ABC 中， A B C   ， (0, )C  ， 所以sin 2sin cosC C B ，且 sin 0C  ， 所以 1cos 2B  ， 因为 (0, )B  ，所以 3B  . （2）因为 2 2BD DC  ，所以 1BD  ， 1CD  ， 3BC  ， - 11 - 因为 ABC 的面积为3 3 ，所以 1 3 sin 3 32 3c   ，解得 4c  ， 由余弦定理得 2 2 2 2 12 cos 4 2 2 4 2 2 33 2AD AB BD AB BD             ， 所以  22 2 2 22 2 3 16AD BD AB     ，即 AD BD ， 所以 2 2 13AC AD BD   ， 所以 13sin 13 CDCAD AC    . 【点睛】本题主要考查正弦定理、余弦定理解三角形，考查三角形的面积公式，考查运算求 解能力，考查数形结合、函数与方程、化归与转化等数学思想. 16. 如图，在四棱锥 PABCD 中，M 是 PA 上的点， ABD△ 为正三角形，CB CD ，PA BD ． （1）求证：平面 MBD  平面 PAC； （2）若 120BCD  ， / /DM 平面 BPC，求证：点 M 为线段 PA 的中点． 【答案】（1）证明见解析；（2）证明见解析. 【解析】 【分析】 （1）取 BD 的中点 O，连结 OA，OC，可证 AC BD ，又由 PA BD ，可得 BD  平面 PAC， 即可得证； （2）取 AB 的中点 N，连结 MN 和 DN，首先可得 AB BC ， DN AB ，所以 DN //BC ，即 可得到 / /DN 平面 BPC．又由 / /DM 平面 BPC，可得平面 / /DMN 平面 BPC．根据面面平行的 性质可得 / /MN PB ，即可得证； 【详解】（1）取 BD的中点 O，连结 OA，OC， - 12 - ∵ ABD△ 为正三角形，∴OA BD ． ∵CB CD ，∴OC BD ． 在平面 ABCD 内，过 O 点垂直于 BD 的直线有且只有一条， ∴A，O，C 三点共线，即 AC BD ． ∵ PA BD ，AC， PA  平面 PAC， AC PA A  ， ∴ BD  平面 PAC．∵ BD  平面 MBD， ∴平面 MBD  平面 PAC． （2）取 AB 的中点 N，连结 MN 和 DN， 因为 120BCD  ，且 BC DC ，所以 30CBD   所以 90ABC  ，即 AB BC ． ∵ ABD△ 为正三角形，∴ DN AB ． 又 DN，BC，AB 共面，∴ / /DN CB ． ∵ DN  平面 BPC，CB  平面 BPC， ∴ / /DN 平面 BPC． ∵ / /DM 平面 BPC，DN， DM  平面 DMN， ∴平面 / /DMN 平面 BPC． ∵ MN  平面 DMN，∴ / /MN 平面 BPC． ∵ MN  平面 PAB，平面 PAB  平面 BPC=PB， ∴ / /MN PB ． ∵N 是 AB 的中点，∴M 为线段 PA 的中点． 【点睛】本题考查面面垂直的证明，线面平行以及面面平行的性质定理及判定定理的应用， 属于中档题. 17. 已知椭圆 2 2 2 2: 1( 0)x yM a ba b     的离心率为 6 3 ，焦距为 2 2 ．斜率为 k 的直线l 与 椭圆 M 有两个不同的交点 A ， B ． - 13 - （1）求椭圆 M 的方程； （2）设 ( 2,0)P  ，直线 PA 与椭圆 M 的另一个交点为C ，直线 PB 与椭圆 M 的另一个交点 为 D ．若C ， D 和点 7 1( , )4 2Q  共线，求 k ． 【答案】（1） 2 2 13 x y  ；（2） 2k  . 【解析】 【分析】 （1）根据离心率和焦距求得 ,c a ，由此求得b ，进而求得椭圆 M 的标准方程. （2）设出直线 PA 的方程，联立直线 PA 的方程和椭圆方程，写出根与系数关系，进而求得C 点的坐标，同理求得 D 点坐标.求得 QC  、QD  ，结合 , ,Q C D 三点共线列方程，化简求得 k 的 值. 【详解】（1）由题意得 2 2 2c  ，所以 2c  ， 又 6 3 ce a   ，所以 3a  ，所以 2 2 2 1b a c   ， 所以椭圆 M 的标准方程为 2 2 13 x y  ． （2）设 1 1( , )A x y ， 2 2( , )B x y ， 3 3( , )C x y ， 4 4( , )D x y ， 则 2 2 1 13 3x y  ①， 2 2 2 23 3x y  ②， 又 ( 2,0)P  ，所以可设 1 1 1 2PA yk k x    ， 直线 PA 的方程为 1( 2)y k x  ， 由 1 2 2 ( 2) 13 y k x x y     消去 y 可得： 2 2 2 2 1 1 1(1 3 ) 12 12 3 0k x k x k     ， 则 2 1 1 3 2 1 12 1 3 kx x k     ，即 2 1 3 12 1 12 1 3 kx xk    ， - 14 - 又 1 1 1 2 yk x   ，代入①式可得 1 3 1 7 12 4 7 xx x    ， 所以 1 3 14 7 yy x   ，所以 1 1 1 1 7 12( , )4 7 4 7 x yC x x     ， 同理可得 2 2 2 2 7 12( , )4 7 4 7 x yD x x     ． 故 3 3 7 1( , )4 2QC x y   ， 4 4 7 1( , )4 2QD x y   ， 因为 , ,Q C D 三点共线， 所以 3 4 4 3 7 1 7 1( )( ) ( )( ) 04 2 4 2x y x y      ， 将点 ,C D 的坐标代入化简可得 1 2 1 2 2y y x x    ， 即 2k  ． 【点睛】本小题主要考查椭圆方程的求法，考查直线与椭圆的位置关系，考查运算求解能力， 属于难题. 18. 某市开发了一块等腰梯形的菜花风景区 ABCD（如图）．经测量， AB 长为 2 百米，CD 长为 6百米， AB 与CD 相距 2 百米，田地内有一条笔直的小路 EF （ E 在 BC 上，F 在 AD 上）与 AB 平行且相距 0.5百米．现准备从风景区入口处 A 出发再修一条笔直的小路 AN 与 BC 交于 N ，在小路 EF 与 AN 的交点 P 处拟建一座瞭望塔． （1）若瞭望塔 P 恰好建在小路 AN 的中点处，求小路 AN 的长； （2）两条小路 EF 与 AN 将菜花风景区划分为四个区域，若将图中阴影部分规划为观赏区．求 观赏区面积 S 的最小值． 【答案】（1） 10 百米；（2）（ 32 4  ）平方百米． 【解析】 【分析】 - 15 - （1）过点 P、N、C 分别做 AB 的垂线，垂足分别为 Q、M、G，在直角三角形 AMN 中，结合勾股 定理，即可求解； （2）以直线 CD 所在直线为 x 轴，边 CD 的垂直平分线为 y 轴建立如图所示的平面直角坐标系， 设 1 3( , ) , [0, )2 2P t t  ，得出面积 21 2 3 2 2 1 t tS t     ，结合基本不等式，即可求解. 【详解】（1）过点 P、N、C 分别做 AB 的垂线，垂足分别为 Q、M、G， 因为 P 是 AN 的中点，所以 2 1MN PQ  ， 由已知条件易知 CBG 是等腰直角三角形，所以 1BM MN  ， 所以 2 1 3AM AB BM     ， 在直角三角形 AMN 中，由勾股定理得 2 2 2 23 1 10AN AM MN     ， 答：小路 AN 的长为 10 百米； （2）以直线 CD 所在直线为 x 轴，边 CD 的垂直平分线为 y 轴建立如图所示的平面直角坐标系， 设 1 3( , ) , [0, )2 2P t t  ，则直线 1: ( 1)2( 1)AP y xt   ， 联立直线 : 1BC y x  ，得 2 2 1Ny t   ， 所以 PEN△ 的高为 2 1 3 2 2 1 2 2(2 1) t t t    ， 所以 21 3 1 1 3 3 2 1 2 3( ) ( )2 2 2 2 2 2(2 1) 2 2 1 t t tS t t t t              ， 令 2 1 [1,4)t m   ，则 21 3 8 1 8 33 24 4 4 m mS mm m              ， 所以当 2 2m  即 12 2t   时，S 的最小值为 32 4  ． - 16 - 答：观赏区面积 S 的最小值为（ 32 4  ）平方百米． 【点睛】本题主要考查了函数的实际应用问题，以及基本不等式的应用问题，其中解答中认 真审题，建立适当的直角坐标系，求得面积的表达式，结合基本不等式求解是解答的关键， 着重考查分析问题和解答问题的能力. 19. 已知函数 ( ) 2 ( 2)x xf x ae e a x    ，（ a R ， e 是自然对数的底数）． （1）讨论 ( )f x 的单调性； （2）当 0x  时， ( ) ( 2)cosf x a x  ，求 a 的取值范围． 【答案】（1）分类讨论，详见解析；（2）[2, ) . 【解析】 【分析】 （1）求得 ( )f x ，然后对 a 分成 0a  和 0a  两种情况进行分类讨论，由此求得  f x 的单调 区间. （2）首先令 2x  ，代入 ( ) ( 2)cosf x a x  ，求得 a 的一个取值范围.构造函数 ( ) ( ) ( 2)cosg x f x a x   ，利用  g x 的导函数 ( )g x 研究  g x 的最小值，由此求得 a 的 取值范围. 【详解】（1） 2 ( 2) 2( ) 2 ( 2) x x x x x ae a ef x ae e a e            2 1x x x ae e e    ， 当 0a  时， ( ) 0f x  ，函数 ( )f x 在 R 上递减； 当 0a  时，由 ( ) 0f x  ，解得 2lnx a  ，故函数 ( )f x 在 2( ,ln )a  上单调递减， - 17 - 由 ( ) 0f x  ，解得 2lnx a  ，故函数 ( )f x 在 2(ln , )a  上单调递增． 综上所述，当 0a  时，  f x 在 R 上递减；当 0a  时，  f x 在 2( ,ln )a  上递减，在 2(ln , )a  上递增. （2）当 2x  时，  2 2( ) 2 ( 2) 0 2 cos2 2 2f ae e a a             ， 即 2 2 2( ) 02e a e        ，故 0a  ， 令 ( ) ( ) ( 2)cosg x f x a x   2 ( 2) c( 2 s) ox xae e a x xa      ， 则 2 2( ) ( 2) ( 2)sin x x aeg x a a xe       ， 若 2a  ，则当 [0, ]x  时， ( ) 0g x  ， 函数 ( )g x 在[0, ] 上单调递增， 当 ( , )x   时， ( ) 2 ( 2) ( 2)x xg x ae e a a       22 4 4 4 04ae e a        ， 当 [0, )x  时， ( )g x 单调递增， 则 ( ) (0) 0g x g  ，符合题意； 若 0 2a  ，则 (0) 2( 2) 0g a    ， ( ) 2 ( 2) ( 2) 2 4x x x xg x ae e a a ae e           ， 由 2 4 0x xae e   得 2 4 2 0ax ln a    ， 故 2 4 2( ) 0ag ln a    ， - 18 - 存在 0 2 4 2(0, ]ax ln a   ，使得 0( ) 0g x  ， 且当 0(0, )x x 时， ( ) 0g x  ， ( )g x 在 0(0, )x x 上单调递减， 当 0(0, )x x 时， ( ) (0) 0g x g  ，不合题意， 综上，实数 a 的取值范围为[2, ) ． 【点睛】本小题主要考查利用导数研究函数的单调性，考查利用导数研究不等式，考查分类 讨论的数学思想方法，属于难题. 20. 已知数列{ }na 是首项为 1 的等差数列，数列{ }nb 是公比不为 1 的等比数列，且满足 1 2 2a a b  ， 2 3 3a a b  ， 4 5 4a a b  （1）求数列{ }na ，{ }nb 的通项公式； （2）令 *2 2 1 1 ( )( 1)( 1) n n n n n n n a bc n Na b a b        ，记数列{ }nc 的前 n 项和为 nS ，求证：对任意 的 *n N ，都有 41 3nS  ； （3）若数列{ }nd 满足 1 1d  ， 1n n nd d b  ，记 1 2 n k n k k dT b   ，是否存在整数  ，使得对任 意的 *n N 都有 2 1 2n n n dT b    成立？若存在，求出  的值；若不存在，说明理由． 【答案】（1） 1 2( 1) 2 1na n n     ， 12 2 2n n nb    ；（2）证明见解析；（3）存在整数 5  ， 使得对任意的 *n N 都有 2 1 2n n n dT b    成立，理由见解析. 【解析】 【分析】 （1）利用等差等比数列的基本量表示已知条件，解方程组得到基本量，利用等差等比数列的 通项公式得到答案； （2）根据（1）的结论得到数列 nc 的通项公式，利用指数的运算裂项，相消求和后得到 nS - 19 - 的表达式，判定单调性，然后利用不等式的基本性质即可证明； （3）假设存在满足要求的整数  ，取 1,2,3n  得到  的范围，进而求得  的值为 5 ，然后证 明当 5  时，对任意的 *n N ，都有 2 1 2n n n dT b    成立．为此先要根据 1n n nd d b  ， 利用等比数列的求和公式，求得 1 14 =2 2 n n nT T        ，结合 1 1 1 1 4 n n n nT T d          ，求得 1 1 15 2 ( )2 4 n n n nT d         ，然后利用作差法证明即可. 【详解】（1）设等差数列{ }na 的公差为 d，等比数列{ }nb 的公比为 q， 则 1 2 1 3 1 2 2 3 2 7 d b q d b q d b q         ，所以 1 2 1 2 ( 1) 4 ( 1) d b q q d b q q      ， 因为 1,0q  ，所以 2q = ． 所以 1 1 1 2 2 2 3 4 2 7 8 d b d b d b         ，解得 1 2d b  所以 1 2( 1) 2 1na n n     ， 12 2 2n n nb    ． （2）因为 2 2 1 1( 1)( 1) n n n n n n n a bc a b a b        2 1 (2 3)2 [(2 1) 2 1] [(2 1) 2 1] n n n n n n           1 1 14 (2 1) 2 1 (2 1) 2 1n nn n            所以 1 2 3n nS c c c c    1 2 2 3 1 1 1 14 ( ) ( )1 1 2 1 3 2 1 3 2 1 5 2               1 1 1( )1 (2 1) 2 1 (2 1) 2n nn n           - 20 - 1 1 1 14 (1 1 2 1 (2 1) 2nn           1 1 1 44( )3 1 (2 1) 2 3nn      又因为对任意的 *n N ，都有 nS 单调递增， 即 1 1 5 8 40 13 13 39nS S c      ， 所以对任意的 *n N ，都有 41 3nS  成立； （3）假设存在满足要求的整数  ， 令 1n  ，则 1 1 2 2 1 2d d b b     ，解得5 9  ； 令 2n  ，则 1 2 2 2 4 4 1 ( ) 2d d d b b b      ，解得 17 33 5 5   ； 令 3n  ，则 1 2 3 3 2 4 6 6 1 ( ) 2d d d d b b b b       ，解得 67 133 23 23   ； 所以 1335 23   ， 又已知 Z  ，故若存在，则 5  ． 下证：当 5  时，对任意的 *n N ，都有 2 1 2n n n dT b    成立． 2 3 1 2 3 1 1 1 1 4 4 4 4 n n nT d d d d                    ； 2 3 1 1 1 2 3 1 1 1 1 1 1 4 4 4 4 4 n n n n nT d d d d d                               2 3 1 1 1 1 2 2 3 1 1 1 1 1 1( ) ( ) ( )4 4 4 4 4 n n n n nT T d d d d d d d                            ； 即 1 2 1 1 1 2 2 3 1 1 1 14 ( ) ( ) ( )4 4 4 n n n n nT T d d d d d d d                          - 21 - 2 3 2 31 1 1 11 2 2 2 24 4 4 4 n n                      2 31 1 1 1 11 22 2 2 2 2 n n                             又 1 1 1 1 4 n n n nT T d          ； 所以 1 1 1 15 2 ( )4 2 n n n n n nT T T d          则 1 1 15 2 ( )2 4 n n n nT d         1 2 2 1 15 2 ( ) ( )2 4 n nn n n n n n d dT db b      1 1 1 12 ( ) ( ) ( )2 4 4 n n n n nd d      1 1 12 ( ) ( ) ( )2 4 n n n nd d      1 12 ( ) ( ) 22 4 n n n    12 2 ( )2 n   而对任意的 *n N ， 12 2 ( )2 n  单调递增， 所以 11 12 2 ( ) 2 2 ( ) 22 2 n      即对任意的 *n N 都有 2 1 5 2n n n dT b    成立，得证. 所以，存在整数 5  ，使得对任意的 *n N 都有 2 1 2n n n dT b    成立． 【点睛】本题考查等差比数列得综合问题，涉及等差等比数列的通项公式，求和公式，裂项 求和法，存在性问题和探索性方法，考查不等式的证明，属难题. 2019—2020 学年江苏省泰州中学高三年级第五次模拟考试 数学第 II 卷 21. 已知矩阵 4 0 0 1A      ， 1 2 0 5B      ，列向量 aX b      . - 22 - （1）求矩阵 AB ； （2）若 1 1 5 1B A X       ，求 a ，b 的值. 【答案】（1） 4 8 0 5      ；（2） 28a  ， 5b  【解析】 试题分析：（1）根据矩阵乘法得矩阵 AB ；（2）根据逆矩阵性质得 5 1X AB      ，再根据矩阵 乘法得结果. 试题解析：（1） 4 0 1 2 4 8 0 1 0 5 0 5AB                  ； （2）由 1 1 5 1B A X       ，解得 5 1X AB      4 8 5 28 0 5 1 5                  ，又因为 aX b      ，所以 28a  ， 5b  . 22. 在平面直角坐标系 xOy 中，曲线 C 的参数方程为 3 cos sin x y      （α为参数），在以坐标 原点 O 为极点，x 轴的正半轴为极轴的极坐标系中，点 M 的极坐标为 32 2, 4      ，直线 l 的极 坐标方程为 sin 2 2 04         ． （1）求直线 l 的直角坐标方程与曲线 C 的普通方程； （2）若 N 是曲线 C 上的动点，P 为线段 MN 的中点，求点 P 到直线l 的距离的最大值． 【答案】（1） 4 0x y   , 2 2 13 x y  ；（2） 7 2 2 . 【解析】 【分析】 （1）直接利用极坐标方程、参数方程和普通方程互化的公式求直线 l 的直角坐标方程与曲线 C 的普通方程；（2）设 N（ 3cos ，sinα），α∈[0，2π）．先求出点 P 到直线 l 的距离 - 23 - 3 1cos sin 62 2 2 d     再求最大值. 【详解】（1）因为直线 l 的极坐标方程为 πsin 2 2 04        ， 即ρsinθ－ρcosθ＋4＝0．由 x＝ρcosθ，y＝ρsinθ， 可得直线 l 的直角坐标方程为 x－y－4＝0． 将曲线 C 的参数方程 3x cos y sin      消去参数 a， 得曲线 C 的普通方程为 2 2 13 x y  ． （2）设 N（ 3cos ，sinα），α∈[0，2π）． 点 M 的极坐标（ 2 2 ， 3π 4 ），化为直角坐标为（－2，2）． 则 3 1cos 1, sin 12 2P        ． 所以点 P 到直线 l 的距离 3 1 πcos sin 6 sin 62 2 3 7 2 22 2 d            ， 所以当 5π 6   时，点 M 到直线 l 的距离的最大值为 7 2 2 ． 【点睛】本题主要考查参数方程、极坐标方程和普通方程的互化，考查三角函数的图像和性 质，考查点到直线的距离的最值的计算，意在考查学生对这些知识的理解掌握水平和分析推 理能力. 23. 在一次运动会上，某单位派出了由 6 名主力队员和 5 名替补队员组成的代表队参加比赛. （1）如果随机抽派 5 名队员上场比赛，将主力队员参加比赛的人数记为 X ，求随机变量 X 的 数学期望； （2）若主力队员中有 2 名队员在练习比赛中受轻伤，不宜同时上场；替补队员中有 2 名队员 身材相对矮小，也不宜同时上场，那么为了场上参加比赛的 5 名队员中至少有 3 名主力队员， 教练员有多少种组队方案？ - 24 - 【答案】(1) 30 11 ；(2) 1 91 【解析】 【分析】 （1）由题可知 X 服从超几何分布，求得 X 的取值，根据概率公式求得对应概率，即可求得 其数学期望； （2）根据题意，将问题根据主力分别有3,4,5 人上场进行分类，即可容易求得. 【详解】（1）由题可知 X 服从超几何分布， X 的可取值为 0,1,2,3,4,5 ， 故可得   5 5 5 11 10 462 CP X C    ；   1 4 6 5 5 11 30 51 462 77 C CP X C     ；   2 3 6 5 5 11 150 252 462 77 C CP X C     ；   3 2 6 5 5 11 200 303 462 11 C CP X C     ；   4 1 6 5 5 11 75 254 462 154 C CP X C     ；   5 6 5 11 6 15 462 77 CP X C     . 故   5 25 100 25 11 2 3 4 577 77 231 154 77E X            630 231 . （2）要满足题意，则可以是 3 名主力 2 名替补；4 名主力 1 名替补；5 名主力. 若是 3 名主力 2 名替补，则共有    3 1 2 2 1 1 4 2 4 3 2 3 144C C C C C C      种； 若是 4 名主力 1 名替补，则共有  4 1 3 1 4 2 4 5 45C C C C    种； 若是 5 名主力，则共有 4 1 4 2 2C C  种； 故要满足题意，共有144 45 2 191   种出场方式. 【点睛】本题考查超几何分布的数学期望的求解，以及组合问题的分类分布求解，属综合中 档题. 24. （1）已知： 1 1 1 m m x n n nC C C    及 1m m n y m C Cn  ，（ 2n  ， *n N ， *)m N ．求 x ； y （结果用 m ， n 表示） （2）已知 0 1 21 1 1 1( ) ( 1)2 3 4 2 n n n n n nf n C C C Cn        ， *n N ．猜想 ( )f n 的表达式 并用数学归纳法证明你的结论． - 25 - 【答案】（1） x m 或 n m ， 1y n  ；（2）猜想 1( ) ( 1)( 2)f n n n    ，证明见解析. 【解析】 【分析】 （1）根据组合数的性质以及组合数公式证明即可； （2）根据 1(1) 6f  ， 1(2) 12f  的值猜想出 1( ) ( 1)( 2)f n n n    ，再由数学归纳法证明即 可. 【详解】（1） 1 1 1 m m m x n n n nC C C C     ，可得 x m 或 n m ； 1 1 1 ! ( 1)! !( )! ( 1)!( ) m m m n n y m m n nC C Cn n m n m m n m           解得 1y n  ； （2） 1 1 1(1) 2 3 6f    ， 1 2 1 1(2) 2 3 4 12f     猜想 1( ) ( 1)( 2)f n n n    下面用数学归纳法证明： ① 1n  时 1 1(1) 6 2 3f    ，猜想成立； ②假设 ( *)n k k N  时猜想成立 即 0 1 21 1 1 1( ) ( 1)2 3 4 2 k k k k k kf k C C C Ck        1 ( 1)( 2)k k    则 1n k  时，由 1 1 1 m m m n n nC C C     及 1 1 m m n n mC Cn    得 0 1 2 1 1 1 1 1 1 1 1 1 1( 1) ( 1)2 3 4 3 k k k k k kf k C C C Ck              0 1 0 2 11 1 1( ) ( )2 3 4k k k k kC C C C C      1 1 1 1 1 1( 1) ( ) ( 1)2 3 k k k k k k k kC C Ck k          0 1 1 11 1 1 1( ) ( 1) ( 1)3 4 2 3 k k k k k k k kf k C C C Ck k           又 1 1 1 1 1 3 3 1 m m k k mC Cm m k       1 1 1 211 3 m kCk m         - 26 - 则 1 2 1 1 1 1 1 2 2 2( 1) ( ) 1 1 11 3 4 3 k k k kf k f k C C Ck k                                     0 1 2 1 1 1 1 1 1( ) ( 1)1 k k k k k kf k C C C Ck                0 1 1 1 1 1 1 2 2 2( 1)2 3 3 k k k k kC C Ck                2( ) ( 1)1f k f kk    即 3 1( 1) ( )1 ( 1)( 2) k f k f kk k k       则 1( 1) ( 2)( 3)f k k k     ，则 1n k  猜想成立． 由①②知 1( ) ( 1)( 2)f n n n    ． 【点睛】本题主要考查了组合公式以及性质的应用，利用数学归纳法证明恒等式，属于中档 题. - 27 -