江苏省南通市2020届高三下学期考前模拟试卷（一）数学试题 Word版含解析 29页

- 1 - 南通市 2020 届高考考前模拟卷（一）数学Ⅰ 一、填空题：本大题共 14 小题，每小题 5 分，共 70 分.请把答案直接填写在答题卡相应位置．．．．．．． 上．. 1. 已知集合  *2, NA x x x x   ∣ ， {0,1,2,3,4}B  ，则 A B ________. 【答案】{1,2,3} 【解析】 【分析】 解不等式确定集合 A ，然后由交集定义计算． 【详解】 2 2 0 ( 1)( 2) 0 0 2 0 4x x x x x x x x                ， 又 *x N ，∴ {1,2,3}A  ，∴ {1,2,3}A B  ． 故答案为：{1,2,3}． 【点睛】本题考查集合的交集运算，考查解无理不等式，属于基础题． 2. 设为虚数单位， (1 2 ) |3 4 |i z i   ，则复数 z 的虚部为________. 【答案】2 【解析】 【分析】 首先将题中所给的式子进行化简，求得 1 2z i  ，从而得到其虚部的值. 【详解】根据 (1 2 ) |3 4 |i z i   ，可得 2 2(1 2 ) 3 4 5i z    ， 所以 2 2 5 5(1 2 ) 1 21 2 1 ( 2) iz ii       ， 所以复数 z 的虚部为 2 ， 故答案为：2. 【点睛】该题考查的是有关复数的问题，涉及到的知识点有复数的除法运算，复数的模，复 数的虚部，属于简单题目. 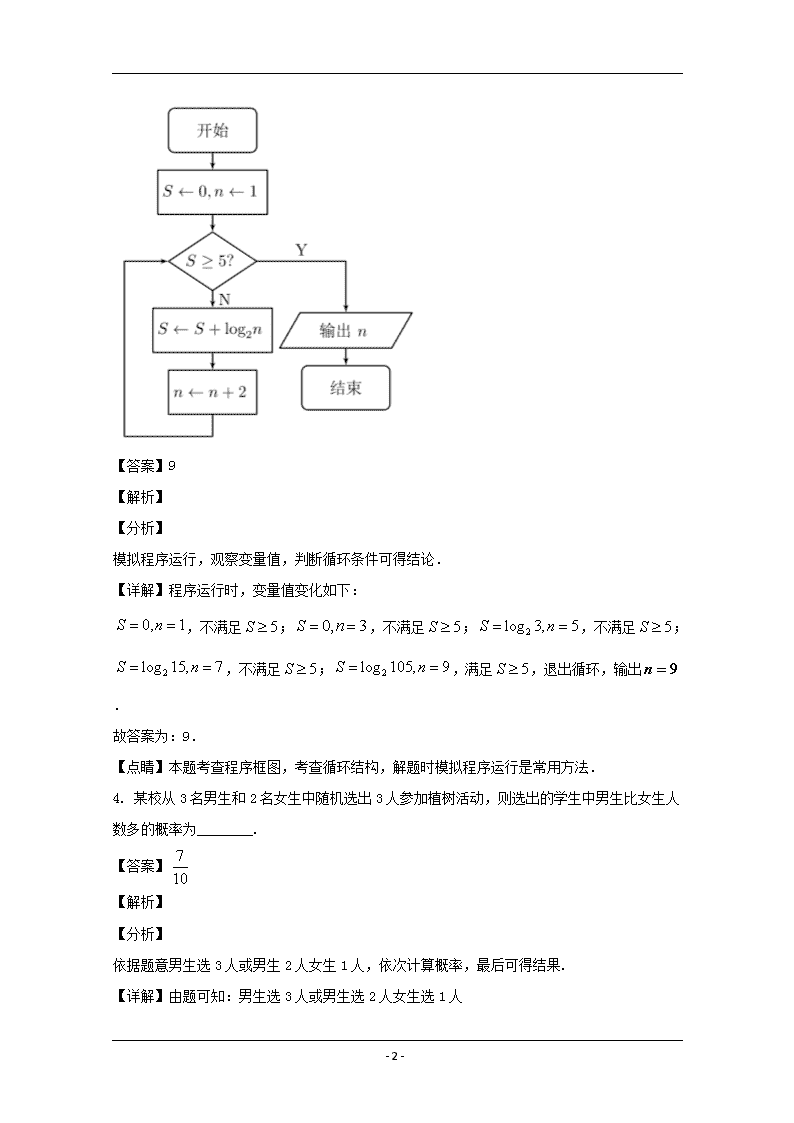3. 若某程序框图如图所示，则运行结果为________. - 2 - 【答案】9 【解析】 【分析】 模拟程序运行，观察变量值，判断循环条件可得结论． 【详解】程序运行时，变量值变化如下： 0, 1S n  ，不满足 5S  ； 0, 3S n  ，不满足 5S  ； 2log 3, 5S n  ，不满足 5S  ； 2log 15, 7S n  ，不满足 5S  ； 2log 105, 9S n  ，满足 5S  ，退出循环，输出 9n  ． 故答案为：9． 【点睛】本题考查程序框图，考查循环结构，解题时模拟程序运行是常用方法． 4. 某校从 3 名男生和 2 名女生中随机选出 3 人参加植树活动，则选出的学生中男生比女生人 数多的概率为________. 【答案】 7 10 【解析】 【分析】 依据题意男生选 3 人或男生 2 人女生 1 人，依次计算概率，最后可得结果. 【详解】由题可知：男生选 3 人或男生选 2 人女生选 1 人 - 3 - 若男生选 3 人，则概率为 3 3 1 3 5 1 10  CP C 若男生选 2 人女生选 1 人，则概率为 2 1 3 2 2 3 5 6 10  C CP C 所以所求的概率为 1 2 7 10   P P P 故答案为： 7 10 【点睛】本题考查互斥事件的概率，审清题意，细心计算，属基础题. 5. 已知抛物线 2 8y x  的焦点与双曲线 2 2 2: 1( 0)xC y aa    的左焦点重合，则双曲线的离 心率为________. 【答案】 2 3 3 【解析】 【分析】 求出抛物线的焦点，由双曲线方程求得 a ，从而可得离心率． 【详解】抛物线 2 8y x  中 2 8p  ， 4p  ，焦点为 ( 2,0) ，它是双曲线的左焦点， 则双曲线 2 2 2: 1( 0)xC y aa    中 2c  ， 2 22 1 3a    ， 所以离心率为 2 2 3 33 ce a    ． 故答案为： 2 3 3 ． 【点睛】本题考查抛物线与双曲线的焦点坐标，考查双曲线的离心率，求出 ,a c 是求双曲线离 心率的基本方法． 6. 为了解某校学生课外阅读的情况，随机统计了 1000 名学生的课外阅读时间，所得数据都 在[50,150]中，其频率分布直方图如图所示，则阅读时间在[125,150) 中的学生人数为 ________. - 4 - 【答案】200 【解析】 【分析】 首先由频率分布直方图求出 25a ，再由人数等于样本总数乘以频率即可求出． 【详解】由题意得： 0.004 0.012 0.016 25 1a     ， 可得 25 0.2a  ， 则阅读时间在[125,150) 中的学生人数为：1000 0.2 200  . 故答案为：200. 【点睛】本题考查频率分布直方图，掌握住频率分布直方图中频率=小矩形的面积．属于较易 题. 7. 已知向量  1,3a  ，  2,1b   ，  3,2c  .若向量 c  与向量 ka b  共线，则实数 k  _________. 【答案】 1 【解析】 【分析】 利用向量的坐标运算求得向量 ka b  的坐标，然后利用平面向量共线的充分必要条件求解. 【详解】∵向量  1,3a  ，  2,1b   ，∴向量  = 2,3 1ka b k k    , 又∵  3,2c  ，且向量 c  与向量 ka b  共线， - 5 - ∴    3 3 1 2 2 ,k k   解得 1k   , 故答案为：   1 . 【点睛】本题考查向量的坐标运算和利用向量共线的充分必要条件求参数的值，考查运算能 力，属基础题. 8. 体积为36 的球的内接正四面体的表面积为________. 【答案】 24 3 【解析】 【分析】 根据球的体积可得球的半径，依题意可知该球为正四面体的外接球，然后计算正四面体的边 长，最后简单计算可得结果. 【详解】由题可知：该球为正四面体的外接球，设球的半径为 R 所以 34 =36 33    R R 如图 另设正四面体的边长为 a 依题意可知O 为该正四面体的球心， N 为 BCD 的中心 所以 3sin 60 2   BM BC a ， 2 3 3 3  BN BM a - 6 - 2 2 6 3    aAN AB BN 所以 2 2 2 OB BN ON ，即 2 2 2 3 6 3 3                aR a R 化简可求得 2 6a  所以该正四面体的表面积为 14 sin 60 24 32     a a 故答案为： 24 3 【点睛】本题考查正四面体的外接球问题，关键在于找到正四面体的边长和外接球半径之间 的关系，属中档题. 9. 设等比数列 na 前 n 项的和为 nS ，满足 16a ， 3a ， 24a 成等差数列，且 4 80S  ，则数列  na 的通项公式为________. 【答案】 12 3n 【解析】 【分析】 先利用等差中项求出公比 q，再利用等比数列前 n 项和求出首项，最后利用等比数列的通项公 式求解即可. 【详解】设公比为 q， 由 16a ， 3a ， 24a 成等差数列， 得 2 3 1 2 1 1 12 6 4 2 6 4a a a a q a a q     ， 又 1 0a  ， 则 22 6 4q q  ，所以 3q  或 1q   ； 又 4 80S  ，所以 1q   ，则 3q  ，    4 4 1 1 4 1 1 1 3 80 21 2 a q a S aq         ， 则 1 1 1 2 3n n na a q     . - 7 - 故答案为： 12 3n . 【点睛】本题主要考查了等差中项，等比数列通项公式以及等比数列前 n 项和公式.属于较易 题. 10. 已知函数 2( )f x x m  ， ( ) 2 lng x n x ，若曲线 ( )y f x 与 ( )y g x 在 1x  处有相 同的切线，则函数 ( ) ( ) ( )F x f x g x  的最小值为________. 【答案】0 【解析】 【分析】 首先对函数 2( )f x x m  和 ( ) 2 lng x n x 求导，代入 1x  ，求得切线的斜率，利用点斜式 求 出 直 线 的 方 程 ， 利 用 两 直 线 重 合 得 到 方 程 组 ， 求 得 1 1 n m     ， 利 用 导 数 研 究 ( ) ( ) ( )F x f x g x  的单调性，确定出最小值，得到结果. 【详解】因为 2( )f x x m  ， ( ) 2 lng x n x ，有 '( ) 2f x x ， 2'( ) ng x x  ， 所以 '(1) 2, '(1) 2f g n  ，且 (1) 1 , (1) 0f m g   ， 所以 ( )y f x 在 1x  处的切线方程为 1 2( 1)y m x    ，即 2 1 0x y m    ， ( )y g x 在 1x  处的切线方程为 0 2 ( 1)y n x   ，即 2 2 0nx y n   ， 因为两条切线相同，所以有 2 2 1 2 n m n      ，解得 1 1 n m     ， 所以 2( ) ( ) ( ) 1 2lnF x f x g x x x     ， ( 0)x  ， 22 2( 1) 2( 1)( 1)'( ) 2 2 x x xF x x x x       ， ( 0)x  ， 所以当 0 1x  时， '( ) 0F x  ，当 1x  时， '( ) 0F x  ， 所以 ( )F x 在(0,1) 上单调递减，在 1, 时单调递增， 所以 ( )F x 在 1x  处取得最小值，且 (1) 1 1 0 0F     ， 故答案为：0. - 8 - 【点睛】该题考查的是有关应用导数研究函数的问题，涉及到的知识点有曲线在某个点处的 切线方程的求解，利用导数研究函数的最值，属于中档题目. 11. 已知 tan 34       ，则 cos 2 4      ________. 【答案】 2 10 【解析】 【分析】 由两角和的余弦公式及二倍角公式求得 cos 2 4     2 2 2 1 tan 2tan 2 1 tan        ，由题意可 求 tan 2  ，代入求解即可. 【详解】由 tan 34       ， 得 tan 1tan 3 tan 24 1 tan              ， 又  2cos 2 cos2 sin 24 2         2 2 2 2 2 cos sin 2sin cos 2 cos sin           2 2 2 1 tan 2tan 2 2 1 tan 10        . 故答案为： 2 10 . 【点睛】本题考查两角和与差的余弦公式，正切齐次式求值，熟记公式，准确化为二次齐次 式是关键，属于中档题. 12. 如图，在 ABC 中， D 、 E 分别是 BC 、 AB 边上的中点， AD 与CE 的交点为O ，若 3AO BC    ， 3 2AB  ，则角 B 的最大值为________. - 9 - 【答案】 4  【解析】 【分析】 表示  1 3     AO AB AC ，进一步可得  1 23     AO BC BA ，然后计算 3AO BC    可得关 于 BC  的一元二次方程，最后利用 0  可得结果. 【详解】根据题意可知：在 ABC 中， D 、 E 分别是 BC 、 AB 边上的中点 所以O 为 ABC 的重心， 所以    2 1 3 1 3 2          AB AC AB ACAO 又 AC BC BA    ，所以  1 23     AO BC BA 又 3AO BC    ， 所以   21 1 22 33 3 3             BC BA BC BC BA BC 根据 3 2AB  ， cos       BA BC BA BC B 所以 21 2 2 cos 3 03     BC B BC 则  2 12 2 cos 4 3 03       B 所以 2 1cos 2 B ，由 3 0     AO BC ，所以 0, 2B     则 2cos 2 B ，所以 0, 4     B 所以 B 的最大值为 4  - 10 - 故答案为： 4  【点睛】本题考查向量的线性表示以及数量积的运算，本题难点在于 21 2 2 cos 3 03     BC B BC 的表示以及 0  的使用和理解，属中档题. 13. 在平面直角坐标系 xOy 中，已知直线 : 6l y kx  上存在点 P ，过点 P 作圆 2 2: 4O x y  的切线，切点分别为  1 1,A x y ，  2 2,B x y ，且 1 2 1 2 2x x y y   ，则实数 k 的 取值范围为________. 【答案】 5 5, ,2 2              【解析】 【分析】 采用数形结合，取 AB 的中点Q ，根据 1 2 1 2 2x x y y   ，可计算 1OQ  ，然后根据 OA OQ OP OA 可得 OP ，最后利用点 O 到直线l 的距离不大于 OP ，可得结果. 【详解】取 AB 的中点Q 如图 根据圆的几何性质可得 △ △Rt OPA Rt OAQ 所以 OA OQ OP OA 由 1 2 1 2,2 2 x x y yQ       ， 所以  2 2 2 2 2 2 1 1 2 2 1 2 1 21 2 1 2 2 2 2 4                   x y x y x x y yx x y yOQ - 11 - 由 2 2 2 2 1 1 2 2 1 2 1 24, 4 2,     x y x y x x y y 所以 1OQ  ，则 4OP  点O 到直线 l 的距离为 2 6 1   d k 则 2 6 54 21       d k k 或 5 2 k 所以 5 5, ,2 2               k 故答案为： 5 5, ,2 2              【点睛】本题考查直线与圆的应用，本题难点在于计算 OP 以及利用关系 d OP ，审清题意， 考查分析能力以及逻辑推理能能力，属难题. 14. 已知函数 3 ln , 0( ) 2 , 0 x x xf x x x x     „ ，若 ( ) ( )g x f x ax  有 3 个零点，则实数 a 的取值 范围为________. 【答案】 11 ,1 (2, )e       【解析】 【分析】 分别画出函数 ( )f x 与 y ax 的图象，根据两图象的交点有 3 个，可得结果. 【详解】由题可知： ( ) ( )g x f x ax  有 3 个零点 等价于函数 ( )f x 与 y ax 的图象有 3 个交点 当 0x  时，   lnf x x x  ，则   1 11 xf x x x     可知若  0,1x ，   0f x  ，则函数单调递减 若  1,x  ，   0f x  ，则函数单调递增 当 0x  时，   3 2 g x x x ，则   23 2 0   g x x 则函数  g x 在 ,0 单调递增 - 12 - 又直线 y ax 恒过原点 如图 当直线 y ax 与   lnf x x x  相切时，设切点为  0 0,A x y   0 0 0 1  xf x x ， 0 0 0ln y x x 所以 0 0 0 0 0 0 ln 1   x x x x ex x ，所以  0 11  f x e 当直线 y ax 与   3 2 g x x x 相切时，切点为原点 所以   23 2  g x x ，则  0 2 g 由函数   lnf x x x  在 0,1 单调递减，在  1, 单调递增 所以    1 1 0  f x f ，所以 lnx x 又函数 ( )f x 与 y ax 的图象有 3 个交点 则 11 ,1 (2, )       a e 故答案为： 11 ,1 (2, )e       【点睛】本题考查根据函数零点个数求参问题，常常使用等价转化的思想，转化为两个函数 交点个数问题，数形结合，解决问题，属中档题. 二、解答题：本大题共 6 小题，共 90 分.请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说 明、证明过程或演算步骤. - 13 - 15. 如图，在斜三棱柱 1 1 1ABC A B C 中， AB AC ， 1AC BC ， 1 / /AC 平面 1ADB . 求证：（1） D 是 BC 的中点； （2）平面 1ADB  平面 1 1BCC B . 【答案】（1）证明见解析；（2）证明见解析. 【解析】 【分析】 （1）连接 1A B 交 1AB 于点 M ，然后根据 1AC //平面 1ADB ，可得 DM // 1AC ，最后根据 M 为 1A B 的中点，可得结果. （2）根据 1AC BC ，可知 DM BC ，可证明 AD BC ，然后根据线面垂直以及面面垂直 的判定定理，可得结果. 【详解】（1）连接 1A B 交 1AB 于点 M 如图 因为 1AC //平面 1ADB ，且 1AC  平面 1A BC - 14 - 平面 1A BC  平面 1=ADB DM ，所以 1AC // DM 又四边形 1 1ABB A 为平行四边形，所以 M 为 1A B 的中点 所以在 1A BC 中， 1AC // DM 且 M 为 1A B 的中点 可知 D 是 BC 的中点 （2）根据（1）可知： 1AC // DM ，又 1AC BC 所以 BC DM ，由 AB AC ， D 是 BC 的中点 所以 BC AD 由 AD DM D , , AD DM 平面 1ADB 所以 BC ⊥平面 1ADB ，又 BC 平面 1 1BCC B 所以平面 1ADB  平面 1 1BCC B 【点睛】本题考查线面平行的性质定理以及面面垂直的判定定理，熟练掌握线线、线面、面 面之间的位置关系以及相关定理，属中档题. 16. 在 ABC 中，已知角 A ， B ，C 所对的边分别为 a ，b ， c . （1）若 3 2b c ， 6cos 3C  ，求 sin A 的值； （2）若 2b  ， 3B  ，求 ABC 面积的最大值. 【答案】（1） 3 6 6  ；（2） 3 . 【解析】 【分析】 （1）由正弦定理求出 sin B ，再利用同角间三角函数关系，两角和的正弦公式和诱导公式可 求得 sin A ； （2）用余弦定理得出 ,a c 的关系式，再由基本不等式可得 ac 的最大值，从而得面积最大值． 【详解】（1）∵ 6cos 3C  ，∴ 3sin 3C  ， 又∵ 3 2b c ，由正弦定理得 sin sin b c B C  ，即 3 3 1sin sin 2 3 2 bB Cc      ， - 15 - ∵ 3 2b c ，∴b c ，∴ B C ，∴ 6B  ， ∴   1 6 3 3 3 6sin sin sin( ) sin cos cos sin 2 3 2 3 6A B C B C B C B C             ； （2）由余弦定理得 2 2 2 2 cosb a c ac B   ，又 3B  ，∴ 2 2 4 2a c ac ac ac ac      ， 当且仅当 ac 时等号成立， ∴ 1 1sin 4 sin 32 2 3ABCS ac B     △ ，∴ ABC 面积最大值为 3 ，此时 ABC 为等 边三角形． 【点睛】本题考查正弦定理和余弦定理，考查两角和的正弦公式，同角间的三角函数关系， 诱导公式等，掌握正弦定理与余弦定理是解题关键，本题属于中档题． 17. 数学家斐波那契在其所著《计算之书》中，记有“二鸟饮泉”间题，题意如下：“如图 1， 两塔相距**步，高分别为**步和**步.两塔间有喷泉，塔顶各有一鸟.两鸟同时自塔顶出发， 沿直线飞往喷泉，同时抵达（假设两鸟速度相同）.求两塔与喷泉中心之距.”如图 2，现有两 塔 AC 、 BD ，底部 A 、 B 相距 12 米，塔 AC 高 3 米，塔 BD 高 9 米.假设塔与地面垂直， 小鸟飞行路线与两塔在同一竖直平面内. （1）若如《计算之书》所述，有飞行速度相同的两鸟，同时从塔顶出发，同时抵达喷泉所在 点 M ，求喷泉距塔底 A 的距离； （2）若塔底 A 、B 之间为喷泉形成的宽阔的水面，一只小鸟从塔顶C 出发，飞抵水面 A 、B 之间的某点 P 处饮水之后，飞到对面的塔顶 D 处.求当小鸟飞行距离最短时，饮水点 P 到塔底 A 的距离. 【答案】（1）9 米；（2）3 米. 【解析】 - 16 - 【分析】 （1）设 AM x ，列方程求解； （2）作出C 关于 AB 的对称点C ，C D 与 AB 的交点就是最短距离的 P 点，由此可计算出 结论． 【详解】（1）设 AM x ，则由题意 2 2 2 23 9 (12 )x x    ，解得 9x  ； （2）设C 是C 关于直线 AB 的对称点，连接C D 交 AB 于 P ， Q 是线段 AB 上任一点，如图，QC QD QC QD C D     ，当且仅当Q 与 P 重合时，等 号成立． P 点即为所求． ∵ ,AC AB BD AB   ，∴ / /AC BD ，∴ AC AP BD BP   ，而 AC AC  ，∴ 3 9 12 AP AP   ， 解得 3AP  ． 【点睛】本题考查数学文化，考查数学的应用，解题关键是正确理解题意，抽象出数学问题， 用相应的数学知识求解． 18. 在平面直角坐标系 xOy 中，已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的离心率 1 2 ，右焦点为 ( ,0)c ，椭圆上的点到准线的距离的最小值为 2， A 为椭圆C 的上顶点，圆 2 2 2 1( ): 4F x c y   ，直线l 与椭圆C 和圆 2F 分别交于点 E ， F ， M ， N . - 17 - （1）求椭圆C 的标准方程； （2）若 AM AN ， 13 48MN EF  ，求直线 l 的方程. 【答案】（1） 2 2 14 3 x y  ；（2） 3 3 3 3y x  或 3 13 3 3 33y x  . 【解析】 【分析】 （1）由离心率和距离的最小值列出关于 ,a c 的方程组，再求出b 可得椭圆方程； （2）由 AM AN 得 2AF MN ，求得直线l 的斜率，然后设直线 l 方程为 3 3y x m  ， 由直线与椭圆相交弦长公式求得弦长 EF ，再由圆的弦长公式求得 MN ，这样由已知可求得 m ． 【详解】（1）由题意 2 1 2 2 c a a ac      ，解得 2 1 a c    ，∴ 2 2 2 22 1 3b a c     ， ∴椭圆标准方程为 2 2 14 3 x y  ； （2）由（1） (0, 3)A ， 2 (1,0)F ， 2 3 0 30 1AFk    ， ∵ AM AN ，∴ A 在线段 MN 的垂直平分线上， 2F 也在线段 MN 的垂直平分线上， ∴ 2AF MN ，∴ 2 1 3 3MN AF k k    ， 设直线l 方程为 3 3y x m  ，设 1 1 2 2( , ), ( , )E x y F x y ， - 18 - 由 2 2 14 3 3 3 x y y x m       得 2 213 8 3 4 12 03 3x mx m    ，∴ 1 2 8 3 13 mx x   ， 2 1 2 12( 3) 13 mx x  ， 2 2 2 1 2 1 2 1 2 48(39 9 )( ) ( ) 4 169 mx x x x x x      ， 2 2 2 1 2 3 2 3 4 3 8 39 91 39 93 3 13 13 mEF x x m              ， 直线方程为 3 03 x y m   ， 2F 到l 直线的距离为 3 1 33 21 13 m m d      ， 由 1 2d  得 1 3 1m  ，即 3 03 m   (*). 圆 2F 半径为 1 2r  ，∴ 2 2 21 312 3 2 32 2 m MN m m                ， ∵ 13 48MN EF  ，∴ 13 48MN EF ， ∴ 2 2 13 8 39 93 2 3 48 13 mm m     ，解得 3 3m   或 13 3 33m   ，满足(*)． ∴直线l 方程是 3 3 3 3y x  或 3 13 3 3 33y x  . 【点睛】本题考查求椭圆的标准方程，考查直线与椭圆相交问题，掌握直线与椭圆相交弦长 公式和直线与圆相交的弦长公式是解题关键．计算的方法是“设而不求”的思想方法，即设 直线方程，设交点坐标，直线方程与椭圆方程联立方程组，消元后应用韦达定理，由韦达定 理的表达式去计算弦长． 19. 已知函数 21( ) ln ( 1)2f x a x x   ， a R . （1）当 2a   时，求函数 ( )f x 的极值； （2）若 [1, )x   ，都有 ( ) 0f x … ，求实数 a 的取值范围； （3）设 21 1( ) ln 2 2 ag x x x x     ，若 0 [1, ]x e  ，使得    0 0f x g x 成立，求实数 a 的 - 19 - 取值范围. 【答案】（1） 1 2ln 22  ；（2）[0, ) ；（3） 2 ( , 1) ,1 e e e        . 【解析】 【分析】 （1）代入 2a   ，求导即可求解极值.（2） [1, )x   ，都有 ( ) 0f x … 等价于 [1, )x   时， min( ) 0f x … 恒成立，然后分类讨论求 min( )f x 即可. (3)令       ( 1)ln am x f x g x a x x x       ，即存在  0 1,x e ，使得  max 0m x  ，然 后分类讨论求  max 0m x  即可求解. 【详解】（1）当 2a   时， 21( ) 2ln ( 1)2f x x x         2 2 12 2'( ) 1 0x xx xf x x xx x x           令 '( ) 0f x  ，解得 1, 2x x   当 0 2x  时， '( ) 0f x  当 2x  时， '( ) 0f x  当 2x  时，  f x 取得极小值   12 2ln 2 2f    ；无极大值. (2) [1, )x   ，都有 ( ) 0f x … ， 即 [1, )x   时， min( ) 0f x … 恒成立     2 ' 1 1a x x af x x xx x       令   2h x x x a   ①当 0  ，即 11 4 0, 4a a   时   0h x  ，  ' 0f x 即 ，所以  f x 在 1, 单增 所以    min 1 0f x f  ，满足题意. - 20 - ②当 0  ，即 11 4 0, 4a a   时 此时 1 1 4 2 ax   ， 1 1 4 2 ax   i）当 1 1 4 12 a   时，即 10 4a  时   0h x  ，  ' 0f x 即 ，所以  f x 在 1, 单增 所以    min 1 0f x f  ，满足题意. ii）当1 1 4 12 a   时，即 0a  时 此时  1 0f  ，所以  min 1 1 4 02 af x f        ，不满足题意. 综上所述：当 0a  时，满足 [1, )x   时， min( ) 0f x … 恒成立.  0,a   （3）令       ( 1)ln am x f x g x a x x x       即存在  0 1,x e ，使得  0 0 0 0 ( 1)ln 0am x a x x x      即存在  0 1,x e ，使得  max 0m x        2 2 2 2 1 11' 1+ x a x a x x aa am x x x x x           i）当 1a  时，此时在  1,x e 上，  ' 0m x  ，  m x 单减    max 1 1 0m x m a      ，即 1a   ，满足题意. ii）当1 a e  时，此时在  1,x a 上，  ' 0m x  ，  m x 单增 在  ,x a e 上，  ' 0m x  ，  m x 单增.      max 1 ln 1m x m a a a a      1 a e  - 21 - 0 ln 1a   即  1 1 ln 1 2a a a a           max 0m x m a   ，不满足题意. iii）当 a e 时， 此时在  1,x e 上，  ' 0m x  ，  m x 单增    max 1 0am x m e a e e        ，解得 2 1 e ea e   ，满足题意. 综上所述： 2 ( , 1) ,1 e ea e         【点睛】此题考查了函数的极值，含参单变量函数任意，存在性条件最值问题，主要用到的 分类讨论的思想方法，属于较难题目. 20. 给定数列 nP ，若 *,m n N  ，且 m n ， m nP P 是数列 nP 的项，则称数列 nP 为 “C 数列”.记数列  na 的前 n 项和为 nS ，且 n N  ，都有  1 2 n n n a aS  . （1）求证：数列  na 为等差数列； （2）若数列  na 为“C 数列”， 1 3a  ， * 2a N ，且 2 3a  ，求 2a 所有的可能值； （3）若 nS 也是数列  na 的项，求证：数列  na 为“C 数列”. 【答案】（1）证明见解析；（2）4 或 6；（3）证明见解析. 【解析】 【分析】 （ 1 ） 由 已 知 得  12 n nS n a a  ，   +1 1 +12 +1n nS n a a  ， 两 式 相 减 得 ： 1 1 12 ( 1)n n na a n a na     ， 1 12 ( 1)n n na a na n a     （ 2n  ）， 两 式 相 减 得 ： 1 12 n n na a a   ，可得证； （2）由（1）得数列  na 为等差数列，设数列  na 的公差为 d,可得 1 2 3 3 6a a d d      ， 32n d   ，讨论 d 的所有可能的值可得 2a 所有的可能值； （3）由已知得当 1n  时， 1 1a S 显然成立，当 2n  时，设 1,n k n mS a S a  ，相减得 n k ma a a  ，即 m n ka a a  ，由等差数列的定义可得证. - 22 - 【详解】（1）证明：当 1n  时，   1 1 1 1 1 1 2 a aa S a    ，成立，又  1 2 n n n a aS  ， 所以  12 n nS n a a  ，   +1 1 +12 +1n nS n a a  ，两式相减得：  1 1 12 ( 1)n n n nS S a n a na      ， 即 1 1 12 ( 1)n n na a n a na     ， 1 12 ( 1)n n na a na n a     （ 2n  ），两式相减得：  1 12( 1) ( 1)n n nn a n a a     ， 即 1 12 n n na a a   ，所以数列  na 为等差数列； （2）由（1）得数列  na 为等差数列，设数列  na 的公差为 d, 由数列  na 为“C 数列”， 1 3a  ， * 2a N ，且 2 3a  ，得 1 2 3 3 6a a d d      ，所 以 6 3 ( 1)d n d    ， 所以 32n d   ，又 n N ，所以 2 21, 5, 4; 3, 3, 6d n a d n a      ， 所以 2a 所有的可能值为 4 或 6； （3）因为 nS 也是数列  na 的项，当 1n  时， 1 1a S 显然成立， 当 2n  时，设 1,n k n mS a S a  ，相减得 n k ma a a  ，即 m n ka a a  ， 又 , ,m n k N  ，所以数列  na 为“C 数列”. 【点睛】本题考查数列的新定义，关键在于理解数列的新定义和运用等差数列的定义、通项 与前 n 项和的关系，得出递推关系式，属于难题. 数学Ⅱ（附加题） 【选做题】本题包括 A、B、C 三小题，请选定其中两小题，并在相应的答题区域内作答．．．．．．．．．．．．．．．．．．．．．，若 多做，则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤. 选修 4-2：矩阵与变换 21. 在平面直角坐标系 xOy 中，曲线 1C 的方程为 2 2 1x y  .设变换 1T 、 2T 对应的矩阵分别 为 1 0 1 1M      ， 1 0 0 2N      ，求曲线 1C 在依次实施变换下 1T 、 2T 后所得曲线 2C 的方程. 【答案】 2 28 4 4x y xy   - 23 - 【解析】 【分析】 根据题中所给的条件，首先求得 2 2 1 0MN      ，之后应用变换公式求得结果. 【详解】因为 1 0 1 1M      ， 1 0 0 2N      ， 所以 2 2 1 0MN      ， 设 ( , )x y 是圆 1C ： 2 2 1x y  上的任意一点，两次变换后对应的点为 ( ', ')x y ， 所以 ' 0 ' 2 2 1 x x y y                 ，所以 ' ' 2 2 x x y x y     ，所以 ' ' 2 ' 2 x x y xy   ， 因为 2 2 1x y  ，所以 2 2' 2 '' ( ) 12 y xx   ，整理得 2 28 ' ' 4 ' ' 4x y x y   ， 曲线 1C 在依次实施变换下 1T 、 2T 后所得曲线 2C 的方程为 2 28 4 4x y xy   . 【点睛】该题考查的是有关矩阵的问题，涉及到的知识点有曲线经过变换之后对应方程的求 解，属于简单题目. 选修 4-4：坐标系与参数方程 22. 在平面直角坐标系 xOy 中，曲线C 的参数方程为 2cos 3 sin x y     （ 为参数）.以原点O 为极点， x 轴的正半轴为极轴建立极坐标系，直线 l 的极坐标方程为 2 sin 14       ， 求直线l 被曲线C 截得的弦长. 【答案】 24 7 【解析】 【分析】 分别写出曲线C 的普通方程与直线l 的直角坐标方程，然后联立方程并使用韦达定理，最后根 据弦长公式进行计算即可. - 24 - 【详解】由题可知：曲线C 的参数方程为 2cos 3 sin x y     （ 为参数） 则曲线C 的普通方程为 2 2 14 3 x y  直线 l 的极坐标方程为 2 sin 14       ， 则 sin cos 1     ，由 sin , cos    y x 所以直线 l 的直角坐标方程为 1 0x y   设两交点分别为    1 1 2 2, , ,A x y B x y 22 2 1 0 7 8 8 0 14 3 x y x xx y          则 1 2 1 2 8 8,7 7x x x x     故所求弦长 2 2 28 81 1 4 4 7 7 7                 AB 故答案为： 24 7 【点睛】本题考查参数方程、极坐标方程以及普通方程的转化，还考查了直线与椭圆的弦长 公式，熟练参数方程、极坐标方程以及普通方程的转化过程，属基础题. 选修 4-5：不等式选讲 23. 设 x ， y ， z 均为正实数，且 4xyz  ，求证： 3 3 3 1 1 1 16 xy yz zx x y y z z x     . 【答案】证明见解析 【解析】 【分析】 由基本不等式 + 2a b ab 可得证. 【详解】因为 x ， y ， z 均为正实数，且 4xyz  ， - 25 - 所以 3 3 16 16 82 2xy xy yzx y x y x      （当且仅当 2 4x y  ，即 x z 时取等号）， 3 3 16 16 82 2yz yz xzy z y z y      （当且仅当 2 4y z  ，即 x y 时取等号）， 3 3 16 16 82 2xz xz xyz x z x z      （当且仅当 2 4z x  ，即 y z 时取等号）， 所以 3 3 3 16 16 16+ + + 2 +2 +2xy yz xz yz xz xyx y y z z x                  （当且仅当 x y z  取等号）， 所以 3 3 3 1 1 1 16 xy yz zx x y y z z x     ，当且仅当 x y z  取等号. 【点睛】本题考查运用基本不等式证明不等式，关键在于构造基本不等式和满足基本不等式 的条件，属于中档题. 【必做题】第 22 题、第 23 题，每题 10 分，共计 20 分.请在答题卡指定区域．．．．．．．内作答，解答时 应写出文字说明、证明过程或演算步骤. 24. 抛物级 2 2 ( 0)x py p  的焦点 F 到直线 2 py   的距离为 2. （1）求抛物线的方程； （2）设直线 1y kx  交抛物线于  1 1,A x y ，  2 2,B x y 两点，分别过 A ， B 两点作抛 物线的两条切线，两切线的交点为 P ，求证： PF AB . 【答案】（1） 2 4x y ；（2）证明见解析 【解析】 【分析】 （1）利用抛物线的定义求出 p 即可得出结论；（2）联立直线和抛物线的方程，得出韦达定理， 设切线 PA 的斜率为 PAk ，切线 PB 的斜率为 PBk ，点 P 坐标为 ,m n ，利用已知条件对函数 21 4y x 求导得出切线的斜率，写出切线方程，求出两切线的交点坐标，利用 1PF ABk k   ， 即可得出结论. 【详解】（1）由题意知： 0, 2 pF      ， - 26 - 则焦点 F 到直线 2 py   的距离为： 22 2 p p p       ， 所以抛物线的方程为： 2 4x y ； （2）证明： 把直线 1y kx  代入 2 4x y 消 y 得： 2 4 4 0x kx   ， 又 216 16 0k    ， 利用韦达定理得 1 2 1 2 4 4 x x k x x       ， 由题意设切线 PA 的斜率为 PAk ，切线 PB 的斜率为 PBk ，点 P 坐标为 ,m n ， 由（1）可得： 21 4y x ， 则 1 2y x  ， 所以 1 2 1 1,2 2PA PBk x k x  ， 则切线 PA 的方程为：  1 1 2y n x x m   ，切线 PA 的方程为：  2 1 2y n x x m   ， 则       1 1 1 2 2 2 1 2 1 2 y n x x m i y n x x m ii         ，    i ii 利用韦达定理化简整理得： 2m k ， 把 2m k 代入  i 整理得： 2 2 2 12 2 22 1 1 1 1 1 1 1 1 2 2 1 2 1 1 1 1 1 1 14 4 14 4 4 4 x xy yn x kx x x x x x xx x x x              ， 则    2 , 1 , 0,1P k F ，  1 1 10 2PF ABk k kk       ， 则 PF AB 【点睛】本题主要考查了利用定义求抛物线的方程，直线与抛物线应用.做这道题的时候要注 - 27 - 意，利用韦达定理，得出两根的关系，设出两切线的交点，认真计算.属于中档题. 25. 设集合   *1,2,3, , N , 2S n n n   ，A 、B 是 S 的两个非空子集，且满足集合 A 中 的最大数不大于集合 B 中的最小数，记满足条件的集合对 ,A B 的个数为 nP . （1）求 2P 的值； （2）求 nP 的表达式. 【答案】（1） 2 5P  ；（2）  1 2 1n nP n   . 【解析】 【分析】 （1）当 2n  时，  1,2S  ，对集合 A 中的最大元素进行分类讨论，确定对应集合 B ，可求 得 2P 的值； （2）设集合 A 中的最大元素为 k ，确定集合 A 、 B 的情况，可得集合 ,A B 共有  1 1 12 2 1 2 2k n k n k      对，由此能求出 nP . 【详解】（1）当 2n  时，  1,2S  . 若  1A  ，则 B 的可能情况为： 1 、 2 、 1,2 ； 若  2A  或 1,2 ，则  2B  . 综上所述， 2 5P  ； （2）若集合 A 中的最大元素为 k ，则集合 A 的其余元素可在1、2 、 、 1k  中任取若干个 （包含不取）， 此时，集合 A 的个数为集合 1,2, , 1k  的子集个数 12k ， 集合 B 中的元素只能在 k 、 1k  、 2k  、 、 n 中任取若干个（至少取一个）， 此时，集合 B 的个数为集合 , 1, 2, ,k k k n   的真子集个数 12 1n k   ， 所以， ,A B 的个数为  1 1 12 2 1 2 2k n k n k      ， 当 k 依次取1、 2 、3 、 、 n 时，可分别得到集合对 ,A B 的个数， 因此， - 28 -          0 1 2 1 2 12 2 2 2 2 2 2 2 2 1 2 2 2n n n n n n n nP n                     1 1 2 2 1 2 11 2 n n nn n         . 【点睛】本题考查集合子集和真子集个数公式的应用，同时也考查了等比数列求和，考查计 算能力，属于中等题. - 29 -