高中数学人教a版必修二 第三章 直线与方程 学业分层测评18 word版含答案 5页

学业分层测评(十八) (建议用时：45 分钟) [达标必做] 一、选择题 1．(2015·淄博高一检测)下列说法正确的是( ) A．经过定点 P0(x0，y0)的直线都可以用方程 y－y0＝k(x－x0)表示 B．经过任意两个不同点 P(x1，y1)、P2(x2，y2)的直线都可以用方程(y－y1)(x2 －x1)＝(x－x1)(y2－y1)表示 C．不经过原点的直线都可以用方程x a ＋y b ＝1 表示 D．经过定点 A(0，b)的直线都可以用方程 y＝kx＋b 表示 【解析】 当直线与 y 轴重合时，斜率不存在，选项 A、D 不正确；当直线垂 直于 x 轴或 y 轴时，直线方程不能用截距式表示，选项 C 不正确；当 x1≠x2，y1≠y2 时由直线方程的两点式知选项 B 正确，当 x1＝x2，y1≠y2 时直线方程为 x－x1＝0， 即(x－x1)(y2－y1)＝(y－y1)(x2－x1)，同理 x1≠x2，y1＝y2 时也可用此方程表示．故选 B. 【答案】 B 2．以 A(1,3)，B(－5,1)为端点的线段的垂直平分线方程是( ) A．3x－y－8＝0 B．3x＋y＋4＝0 C．3x－y＋6＝0 D．3x＋y＋2＝0 【解析】 kAB＝ 1－3 －5－1 ＝1 3 ，AB 的中点坐标为(－2,2)，所以所求方程为：y－ 2＝－3(x＋2)，化简为 3x＋y＋4＝0. 【答案】 B 3．若直线 ax＋by＋c＝0 经过第一、二、三象限，则( ) A．ab>0，bc>0 B．ab>0，bc>0 C．ab<0，bc>0 D．ab<0，bc<0 【解析】 直线经过第一、二、三象限， 则由 y＝－a b x－c b 可知， －a b>0， －c b>0 ⇒ ab<0， bc<0， 选 D. 【答案】 D 4．已知直线 l1：(k－3)x＋(3－k)y＋1＝0 与直线 l2：2(k－3)x－2y＋3＝0 垂直， 则 k 的值是( ) 【导学号：09960111】 A．2 B．3 C．2 或 3 D．2 或－3 【解析】 ∵l1⊥l2，∴2(k－3)2－2(3－k)＝0， 即 k2－5k＋6＝0，得 k＝2 或 k＝3. 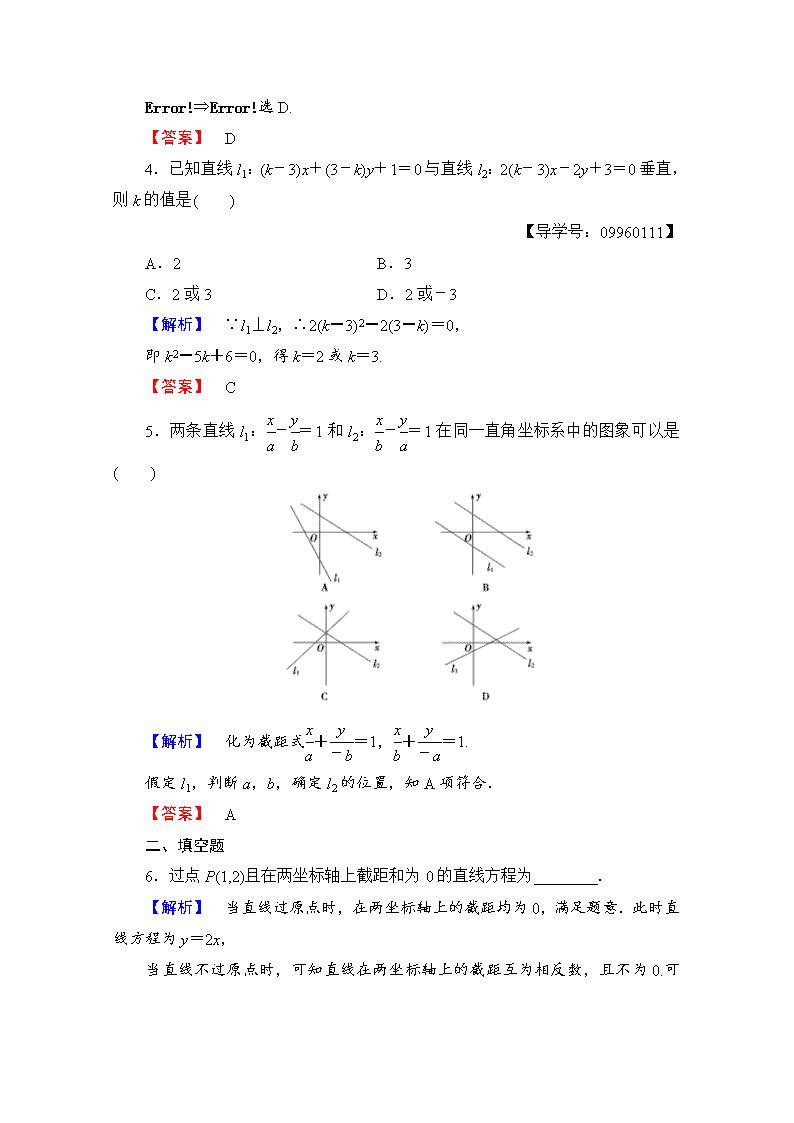【答案】 C 5．两条直线 l1：x a －y b ＝1 和 l2：x b －y a ＝1 在同一直角坐标系中的图象可以是 ( ) 【解析】 化为截距式x a ＋ y －b ＝1，x b ＋ y －a ＝1. 假定 l1，判断 a，b，确定 l2 的位置，知 A 项符合． 【答案】 A 二、填空题 6．过点 P(1,2)且在两坐标轴上截距和为 0 的直线方程为________． 【解析】 当直线过原点时，在两坐标轴上的截距均为 0，满足题意．此时直 线方程为 y＝2x， 当直线不过原点时，可知直线在两坐标轴上的截距互为相反数，且不为 0.可 设直线方程为x a ＋ y －a ＝1，即 x－y＝a，因为直线过 P(1,2)，所以 1－2＝a，所以 a ＝－1，直线方程为 x－y＋1＝0 【答案】 y＝2x 或 x－y＋1＝0 7．垂直于直线 3x－4y－7＝0，且与两坐标轴围成的三角形的面积为 6 的直线 在 x 轴上的截距是________． 【解析】 设直线方程是 4x＋3y＋d＝0， 分别令 x＝0 和 y＝0， 得直线在两坐标轴上的截距分别是－d 3 、－d 4 ， ∴6＝1 2 ×|－d 3|×|－d 4|＝d2 24. ∴d＝±12，则直线在 x 轴上的截距为 3 或－3. 【答案】 3 或－3 三、解答题 8．若方程(m2－3m＋2)x＋(m－2)y－2m＋5＝0 表示直线． (1)求实数 m 的范围； (2)若该直线的斜率 k＝1，求实数 m 的值． 【导学号：09960112】 【解】 (1)由 m2－3m＋2＝0， m－2＝0， 解得 m＝2， 若方程表示直线，则 m2－3m＋2 与 m－2 不能同时为 0，故 m≠2. (2)由－m2－3m＋2 m－2 ＝1，解得 m＝0. 9．已知三角形的三个顶点 A(0,4)，B(－2,6)，C(－8,0)． (1)求三角形三边所在直线的方程； (2)求 AC 边上的垂直平分线的方程． 【解】 (1)直线 AB 的方程为y－4 6－4 ＝ x－0 －2－0 ， 整理得 x＋y－4＝0； 直线 BC 的方程为y－0 6－0 ＝ x＋8 －2＋8 ，整理得 x－y＋8＝0； 由截距式可知，直线 AC 的方程为 x －8 ＋y 4 ＝1，整理得 x－2y＋8＝0. (2)线段 AC 的中点为 D(－4,2)，直线 AC 的斜率为1 2 ，则 AC 边上的垂直平分线 的斜率为－2，所以 AC 边的垂直平分线的方程为 y－2＝－2(x＋4)，整理得 2x＋y＋6＝0. [自我挑战] 10．(2016·潍坊高一检测)已知两直线的方程分别为 l1：x＋ay＋b＝0，l2：x＋ cy＋d＝0，它们在坐标系中的位置如图 323 所示，则( ) 图 323 A．b>0，d<0，a0，d<0，a>c C．b<0，d>0，a>c D．b<0，d>0，a0，k2＝－1 c>0 且 k1>k2，∴a<0，c<0 且 a>c. 又 l1 的纵截距－b a<0，l2 的纵截距－d c>0， ∴b<0，d>0，故选 C. 【答案】 C 11．直线过点 P 4 3 ，2 且与 x 轴、y 轴的正半轴分别交于 A，B 两点，O 为坐 标原点，是否存在这样的直线同时满足下列条件： (1)△AOB 的周长为 12； (2)△AOB 的面积为 6. 若存在，求出直线的方程；若不存在，请说明理由． 【导学号：09960113】 【解】 设直线方程为x a ＋y b ＝1(a>0，b>0)， 若满足条件(1)，则 a＋b＋ a2＋b2＝12. ① 又∵直线过点 P 4 3 ，2 ，∴ 4 3a ＋2 b ＝1. ② 由①②可得 5a2－32a＋48＝0， 解得 a＝4， b＝3 或 a＝12 5 ， b＝9 2 ， ∴所求直线的方程为x 4 ＋y 3 ＝1 或5x 12 ＋2y 9 ＝1， 即 3x＋4y－12＝0 或 15x＋8y－36＝0. 若满足条件(2)，则 ab＝12， ③ 由题意得： 4 3a ＋2 b ＝1， ④ 由③④整理得 a2－6a＋8＝0， 解得 a＝4， b＝3 或 a＝2， b＝6， ∴所求直线的方程为x 4 ＋y 3 ＝1 或x 2 ＋y 6 ＝1， 即 3x＋4y－12＝0 或 3x＋y－6＝0. 综上所述：存在同时满足(1)(2)两个条件的直线方程，为 3x＋4y－12＝0.