新教材数学人教B版必修第二册课件：6-2-2　向量的减法运算 30页

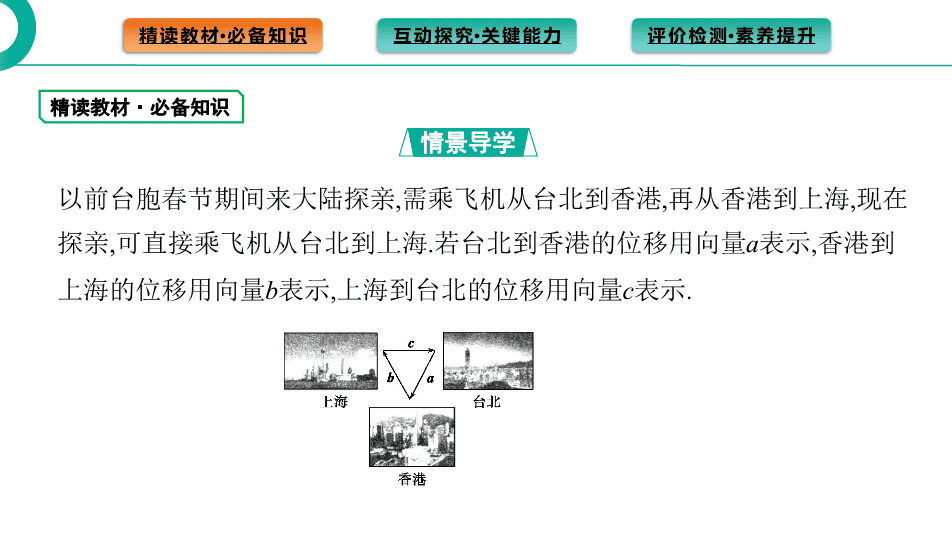
精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 第六章　平面向量及其应用 §6.2　平面向量的运算 6.2.2　向量的减法运算 第 一 篇 教 材 过 关 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 以前台胞春节期间来大陆探亲,需乘飞机从台北到香港,再从香港到上海,现在 探亲,可直接乘飞机从台北到上海.若台北到香港的位移用向量a表示,香港到 上海的位移用向量b表示,上海到台北的位移用向量c表示. 情景导学 精读教材·必备知识 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 问题1:向量a、b、c有何关系? 答案 a+b+c=0. 问题2:现在探亲的位移是什么? 答案　位移的方向与c的方向相反,大小为|c|. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1.相反向量 (1)定义:与向量a长度① ,方向② 的向量,叫做a的相反向量,记作-a. (2)性质:a+(-a)=(-a)+a=0. 如果a,b互为相反向量,那么a=-b,b=-a,a+b=0. 零向量的相反向量仍是③ . 思考1:相反向量的两个要素是什么? 教材研读 相等 相反 零向量 提示　方向相反,长度相等. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.向量的减法 (1)定义:求两个向量差的运算叫做向量的减法.a-b=a+(-b),即减去一个向量相 当于加上这个向量的④ . (2)作法:已知向量a,b,在平面内任取一点O,作  =a,  =b,则  =a-b,如图所示:   OA  OB  BA  相反向量 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 (3)几何意义:如果把两个向量a、b的起点放在一起,则a-b可以表示为从向量b 的⑤ 指向向量a的⑥ 的向量. 思考2:作向量减法时,差向量如何表示? 终点 终点 提示　连接两向量终点,箭头指向被减向量. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究一　向量的减法运算 互动探究·关键能力 例1　化简:(1)(  -  )-(  -  ); (2)(  +  +  )-(  -  -  ). AB  CD  AC  BD  AC  BO  OA  DC  DO  OB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)解法一:(统一成加法) (  -  )-(  -  ) =  -  -  +  =  +  +  +  =(  +  )+(  +  )=  +  =0. 解法二:(利用减法) (  -  )-(  -  )=  -  -  +  =(  -  )-  +  =  -  +  =  +  =0. 解法三:(利用  =  -  )设O是平面内任意一点, AB  CD  AC  BD  AB  CD  AC  BD  AB  DC  CA  BD  AB  BD  DC  CA  AD  DA  AB  CD  AC  BD  AB  CD  AC  BD  AB  AC  CD  BD  CB  CD  BD  DB  BD  AB  OB  OA  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 则(  -  )-(  -  )=  -  -  +  =(  -  )-(  -  )-(  -  )+(  -  ) =  -  -  +  -  +  +  -  =0. (2)(  +  +  )-(  -  -  ) =(  +  )-(  -  )=  -  =0. AB  CD  AC  BD  AB  CD  AC  BD  OB  OA  OD  OC  OC  OA  OD  OB  OB  OA  OD  OC  OC  OA  OD  OB  AC  BO  OA  DC  DO  OB  AC  BA  OC  OB  BC  BC  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 向量减法运算的常用方法   精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 特别提醒 掌握向量加、减法的定义及向量加法的交换律、结合律等基础知识,可以将 杂乱的向量运算有序化处理. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 1-1　化简:(1)  -  +  ; (2)  +  +  -  -  . OA  OD  AD  AB  DA  BD  BC  CA  解析　(1)解法一:  -  +  =  +  =0. 解法二:  -  +  =  +  -  =  -  =0. (2)  +  +  -  -  =  +  +  +  +  =(  +  )+(  +  )+  =  +   +  =  +  +  =0+  =  . OA  OD  AD  DA  AD  OA  OD  AD  OA  AD  OD  OD  OD  AB  DA  BD  BC  CA  AB  DA  BD  CB  AC  AB  BD  AC  CB  DA  AD  AB  DA  AD  DA  AB  AB  AB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究二　利用已知向量表示其他向量 例2 (易错题)如图所示,四边形ACDE是平行四边形,B是该平行四边形外一点, 且  =a,  =b,  =c,试用向量a,b,c表示向量  ,  ,  .   AB  AC  AE  CD  BC  BD  解析　因为四边形ACDE是平行四边形,所以  =  =c,  =  -  =b-a,   =  +  =b-a+c. CD  AE  BC  AC  AB  BD  BC  CD  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 变式训练 1.(变结论)试用向量a,b,c表示  与  . BE  CE  解析   =  -  =c-a,   =  -  =c-b. BE  AE  AB  CE  AE  AC  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.(变条件)若将“点B是平行四边形ACDE外一点”换为“点B是平行四边形 ACDE内一点”,其他条件不变,其结论又如何呢?   解析　因为四边形ACDE是平行四边形, 所以  =  =c,  =  -  =b-a,   =  +  =b-a+c. CD  AE  BC  AC  AB  BD  BC  CD  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 易错点拨 常因错误地使用向量的减法法则而失分. 减法口诀:起点相同,连接终点,箭头指向被减向量. 把起点相同的放在一起计算.必要时,可画出图形,结合图形观察可使问题更为 直观. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究三　向量减法的几何意义 例3　(1)在菱形ABCD中,∠A=60°,|  |=2,则|  -  |=　　　 . (2)若|  |=8,|  |=5,则|  |的取值范围是　　　 . AB  BC  DC  AB  AC  BC  2 [3,13] 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)如图所示,连接BD,   ∵  -  =  -  =  , 且四边形ABCD为菱形,∠A=60°,∴△ABD为正三角形, ∴|  |=|  |=2. BC  DC  AD  AB  BD  BD  AB  故|  -  |=2. (2)由  =  +  及三角不等式,得|  |-|  |≤|  +  |≤|  |+|  |,又因为|  |= |  |=8,所以3≤|  +  |=|  |≤13,即|  |∈[3,13]. BC  DC  BC  BA  AC  BA  AC  BA  AC  BA  AC  BA  AB  BA  AC  BC  BC  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 向量a+b,a-b的几何意义 先对向量条件化简、转化,再找(作)图形(三角形或平行四边形),确定图形的形 状,最后利用图形的几何性质求解. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 3-1　已知|a|=6,|b|=8,且|a+b|=|a-b|,求|a-b|. 解析　如图,作  =a,  =b,再以OA,OB为邻边作平行四边形OACB,则有  =a +b,  =a-b,   即|a+b|与|a-b|是平行四边形的两条对角线的长度,又因为|a+b|=|a-b|,所以该四 边形为矩形,从而|a-b|=  =10. OA  OB  OC  BA  2 26 8 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1.下列等式中,正确的个数是  (　 　) ①0-a=-a;②-(-a)=a; ③a+(-a)=0;④a+0=a;⑤a-b=a+(-b); ⑥a+(-a)=0.  A.3　 B.4　 C.5　 D.6 课堂检测 评价检测·素养提升 C 解析　只有⑥不正确. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.在△ABC中,  =a,  =b,则  =  (　　) A.a-b　　B.b-a　　C.a+b　　D.-a-b BC  CA  AB  D 解析   =  -  =-  -  =-a-b.AB  CB  CA  BC  CA  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3.如图所示,已知正六边形ABCDEF,O是它的中心,其中  =a,  =b,  =c,则   等于  (　 　)   A.a+b　　B.b-a　　C.c-b　　D.b-c DE  OB  OC  EF  解析   =  =  -  =b-c.EF  CB  OB  OC  D 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 4.已知  =a,  =b,  =c,  =d,且四边形ABCD为平行四边形,则  (　　) A.a+b+c+d=0　　B.a-b+c-d=0 C.a+b-c-d=0　　 D.a-b-c+d=0 OA  OB  OC  OD  B 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　如图,a-b=  -  =  ,   c-d=  -  =  , 因为四边形ABCD为平行四边形, 所以  =  ,即  -  =0, 所以  +  =0,即a-b+c-d=0. OA  OB  BA  OC  OD  DC  BA  CD  BA  CD  BA  DC  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 5.依据图形,解答下列各题:   (1)用a、d、e表示  ; (2)用b、c表示  ; (3)用a、b、e表示  ; DB  DB  EC  (4)用c、d表示  . EC  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)  =  +  +  =d+e+a. (2)  =  -  =-  -  =-b-c. (3)  =  +  +  =e+a+b. (4)  =-  =-(  +  )=-c-d. DB  DE  EA  AB  DB  CB  CD  BC  CD  EC  EA  AB  BC  EC  CE  CD  DE  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 直观想象——利用几何图形的性质判断 已知O为四边形ABCD所在平面外的一点,且向量  ,  ,  ,  满足  +  =   +  ,则四边形ABCD的形状为　　　 . OA  OB  OC  OD  OA  OC  OB  OD  素养演练 平行四边形 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　∵  +  =  +  ,∴  -  =  -  , ∴  =  ,∴|  |=|  |,且DA∥CB, ∴四边形ABCD是平行四边形. 素养探究:向量a+b,a-b的几何意义表示的是平行四边形的对角线,所以要熟悉 并会应用平行四边形、菱形、矩形、正方形对角线具有的性质,解题过程中 体现了直观想象的核心素养. OA  OC  OB  OD  OA  OD  OB  OC  DA  CB  DA  CB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 针对训练 　已知  =a,  =b,若|  |=5,|  |=12,且∠AOB=90°,则|a-b|=　　　 .OA  OB  OA  OB  13 解析　如图所示:   在矩形OACB中,  -  =  , 则|a-b|=|  |=  =  =13. OA  OB  BA  BA  2 2| | | |a b 2 25 12