2018-2019学年湖南省五市十校教研教改共同体高一12月联考数学试题 11页

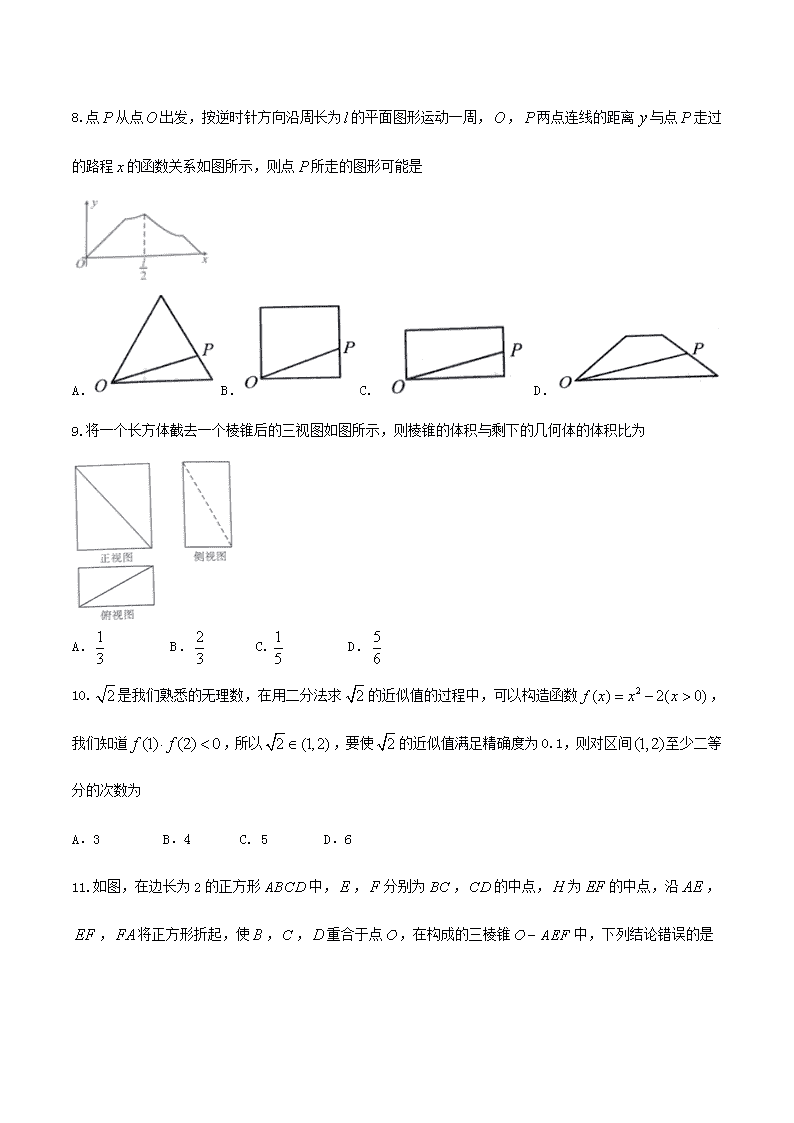
‎2018-2019学年湖南省五市十校教研教改共同体高一12月联考数学试题 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.设集合，，则 A． B． C． D．‎ ‎2.下列函数与函数的图像相同的是 A． B． C． D．‎ ‎3.下列结论正确的是 A．相等的角在直观图中仍然相等 B．相等的线段在直观图中仍然相等 ‎ C．水平放置的三角形的直观图是三角形 D．水平放置的菱形的直观图是菱形 ‎ ‎4.已知函数，则 A． B． C. D．‎ ‎5.函数的值域是 A． B． C. D．‎ ‎6.若函数是定义在上的奇函数，且当时，（为常数），则 A． B． C. D．‎ ‎7.已知函数，设，，，，则 A． B． ‎ C. D．，，的大小关系不能确定 ‎8.点从点出发，按逆时针方向沿周长为的平面图形运动一周，，两点连线的距离与点走过的路程的函数关系如图所示，则点所走的图形可能是 A．B．C. D．‎ ‎9.将一个长方体截去一个棱锥后的三视图如图所示，则棱锥的体积与剩下的几何体的体积比为 A． B． C. D．‎ ‎10.是我们熟悉的无理数，在用二分法求的近似值的过程中，可以构造函数，我们知道，所以，要使的近似值满足精确度为0.1，则对区间至少二等分的次数为 A．3 B．4 C. 5 D．6‎ ‎11.如图，在边长为2的正方形中，，分别为，的中点，为的中点，沿，，将正方形折起，使，，重合于点，在构成的三棱锥中，下列结论错误的是 A．平面 ‎ B．三棱锥的体积为 ‎ C. 直线与平面所成角的正切值为 ‎ D．异面直线与所成角的余弦值为 ‎ ‎12.中国古代名词“刍童”原来是草堆的意思，关于“刍童”体积计算的描述，《九章算术》注曰：“倍上袤，下袤从之，亦倍下袤，上袤从之，各以其广乘之，并，以高乘之，皆六而一．”其计算方法是：将上底面的长乘二，与下底面的长相加，再与上底面的宽相乘，将下底面的长乘二，与上底面的长相加，再与下底面的宽相乘；把这两个数值相加，与高相乘，再取其六分之一.已知一个“刍童”的下底面是周长为18的矩形，上底面矩形的长为3，宽为2，“刍童”的高为3，则该“刍童”的体积的最大值为 ‎ A． B． C. 39 D．‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.若幂函数的图像过点，则的解析式为 ．‎ ‎14.表面积为24的正方体的外接球的体积为 ．‎ ‎15.已知，是两个不同平面，，是平面及外的两条不同直线，给出以下四个论断：①；②；③；④.以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题为 ．‎ ‎16.设函数，则满足的的取值范围是 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.（1）求值：；‎ ‎（2） 若，，用，表示.‎ ‎18. 如图，在圆锥中，是其底面圆的直径，点在底面圆周上运动（不与，重合），为的中点.‎ ‎（1）证明：平面；‎ ‎（2）证明：平面平面.‎ ‎19. 已知函数，，其中且.‎ ‎（1）求函数的定义域；‎ ‎（2）若函数的最大值是2，求的值；‎ ‎（3）求使成立的的取值范围.‎ ‎20. 如图，四棱锥中，，平面，，.‎ ‎（1）证明：；‎ ‎（2）若四面体的体积为，求四棱锥的侧面积.‎ ‎21. 小萌大学毕业后，家里给了她10万元，她想办一个“萌萌”加工厂，根据市场调研，她得出了一组毛利润（单位：万元）与投入成本（单位：万元）的数据如下：‎ 投入成本 ‎0.5‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 毛利润 ‎1.06‎ ‎1.25‎ ‎2‎ ‎3.25‎ ‎5‎ ‎7.25‎ ‎9.98‎ 为了预测不同投入成本情况下的利润，她想在两个模型，中选一个进行预测.‎ ‎（1）根据投入成本2万元和4万元的两组数据分别求出两个模型的函数解析式，请你根据给定数据选出一个较好的函数模型进行预测（不必说明理由），并预测她投入8万元时的毛利润；‎ ‎（2）若小萌准备最少投入2万元开办加工厂，请预测加工厂毛利润率的最大值，并说明理由.（）‎ ‎22.已知函数在区间上的值域为.‎ ‎（1）求的值；‎ ‎（2）若不等式对任意的恒成立，求实数的取值范围；‎ ‎（3）若函数有3个零点，求实数的值. ‎ 试卷答案 一、选择题 ‎1-5：BDCAC 6-10： DACCB 11、12：DB 二、填空题 ‎13. 14. ‎ ‎15. ①③④②；②③④①（任选一个即可） 16.‎ 三、解答题 ‎17.（1）原式 ‎（2）∵，，∴，‎ ‎∴‎ ‎18. 证明：（1）∵为的中点，圆心为的中点，∴，‎ ‎∵平面，平面，‎ ‎∴平面.‎ ‎（2）∵，是的中点，∴.‎ ‎∵底面，底面，∴，‎ ‎∵，，平面，‎ ‎∴平面，‎ ‎∵平面，‎ ‎∴平面平面.‎ ‎19.（1）要使的表达式有意义，‎ 则有：‎ ‎∴函数的定义域是 ‎（2）令，‎ 则 设，则，‎ ‎∵函数的最大值是2.‎ 即，的最大值是2.‎ ‎∴且，∴‎ ‎∴‎ ‎（3）由即 Ⅰ：若，则 ‎ ∴‎ Ⅱ：若，则有：‎ ‎∴‎ ‎∴时满足题意的的取值范围是 时满足题意的的取值范围是 ‎20.（1）证明：在中，，，‎ ‎∴，∴即：‎ ‎∵平面，平面，∴，‎ ‎∵，∴平面，‎ ‎∵平面，∴‎ ‎（2）解由（1）知平面 ‎∴，‎ ‎∴，‎ ‎∵，平面，‎ ‎∴平面，又平面，∴，∴，‎ 又在直角梯形中，，∴‎ 在直角三角形中，‎ ‎∴‎ ‎∴四棱锥的侧面积为 ‎21. 解：（1）先求第一个模型的解析式，‎ 由已知数据可得，解得，‎ ‎∴，‎ 同理可求得 选择作为较好的模型，‎ 当万元时，万元.‎ ‎（2）由已知，‎ 设，则，，‎ ‎∵，∴，，‎ ‎∴，在上是增函数，‎ 当万元时，.‎ ‎22. 解：（1）依题意，的最大值必然是在区间的端点处取得，‎ 所以：或，解得：，‎ 经检验，符合题意.‎ ‎（2）令，则原不等式可化为：恒成立.‎ ‎∴，∴的取值范围是 ‎（3）令，则可化为：‎ ‎∵解方程可得：或 又依题意：有3个不同的零点，‎ ‎∴，‎ ‎∴‎