2019-2020学年江西省南昌市实验中学高一上学期第一次月考数学试题Word版含答案 13页

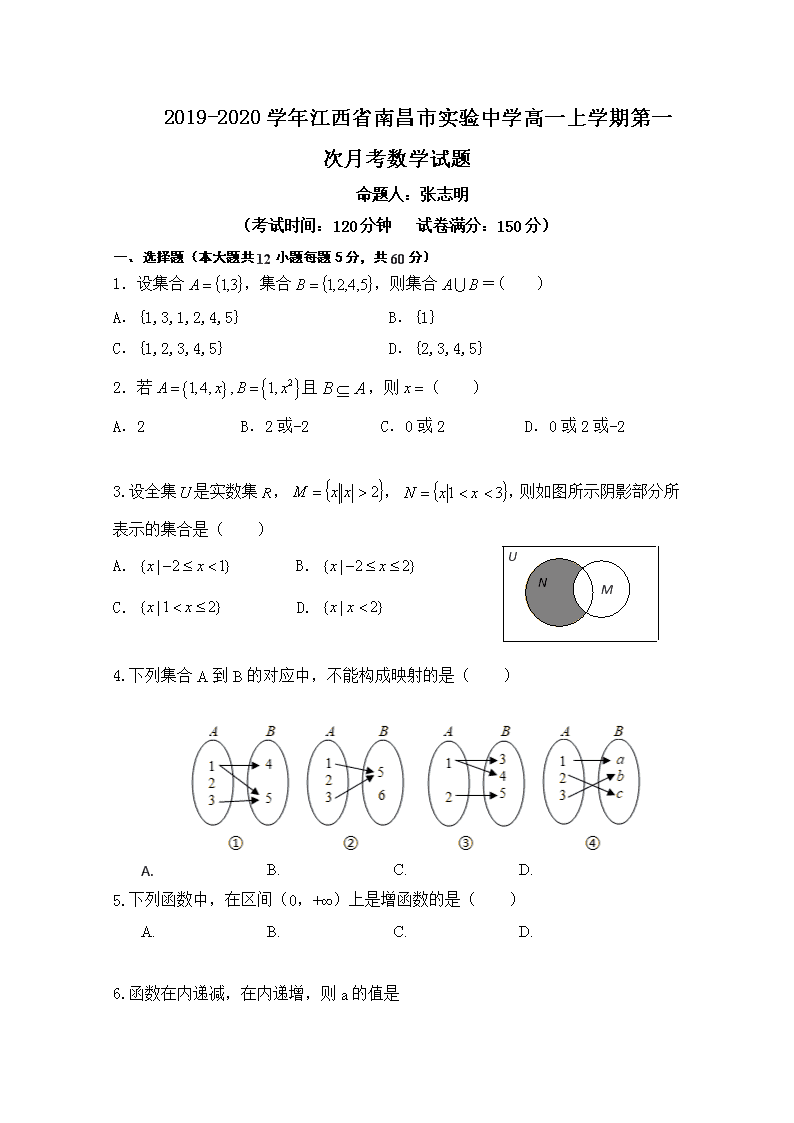
2019-2020 学年江西省南昌市实验中学高一上学期第一 次月考数学试题 命题人：张志明 （考试时间：120 分钟 试卷满分：150 分） 一、选择题（本大题共 12 小题每题 5 分，共 60 分） 1．设集合 ，集合 ，则集合 ＝(　　)　 A．{1,3,1,2,4,5} B．{1} C．{1,2,3,4,5} D．{2,3,4,5} 2．若 且 ，则 （ ) A．2 B．2 或-2 C．0 或 2 D．0 或 2 或-2 3.设全集 是实数集 ， ， ，则如图所示阴影部分所 表示的集合是（ ） A． B． C． D． 4.下列集合 A 到 B 的对应中，不能构成映射的是（　　） A. B. C. D. 5.下列函数中，在区间（0，+∞）上是增函数的是（　　） A. B. C. D. 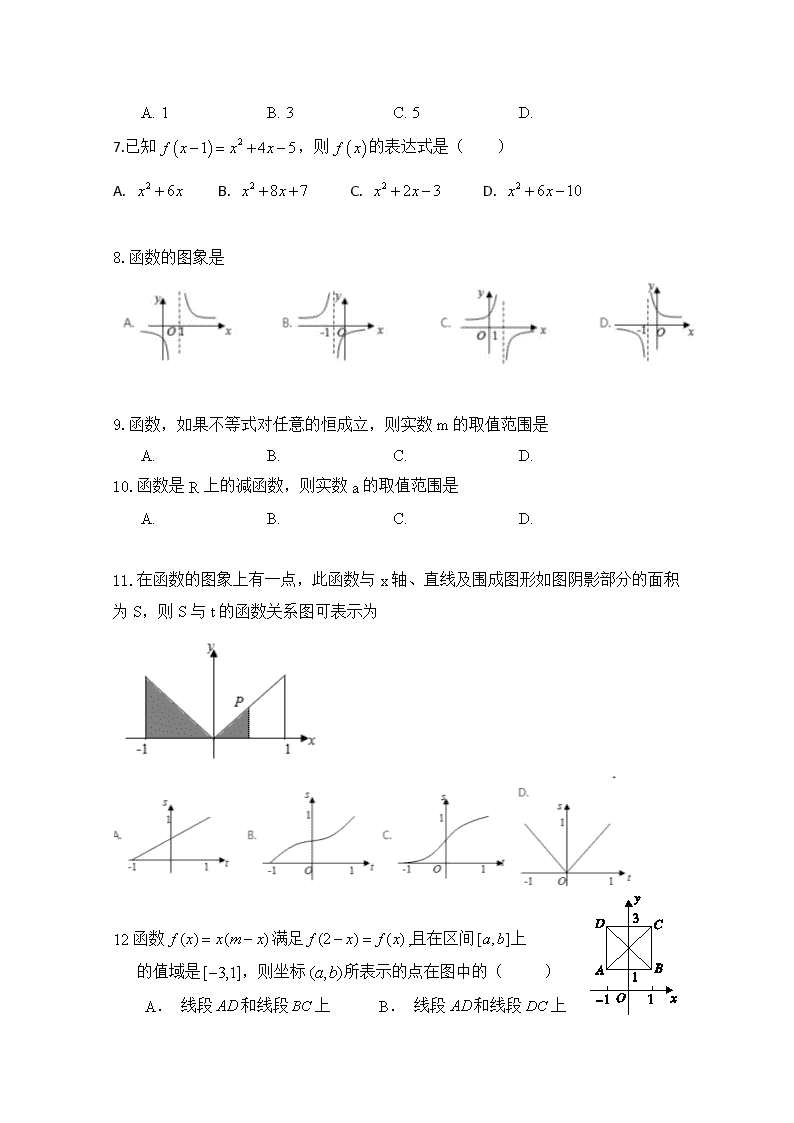6.函数在内递减，在内递增，则 a 的值是　　 { }3,1=A { }5,4,2,1=B BA  { } { }21,4, , 1,A x B x= = AB ⊆ x = U R { }2>= xxM { }31 <<= xxN { | 2 1}x x− ≤ < { | 2 2}x x− ≤ ≤ { |1 2}x x< ≤ { | 2}x x < U N M A. 1 B. 3 C. 5 D. 7.已知 ，则 的表达式是（ ） A. B. C. D. 8.函数的图象是　　 9.函数，如果不等式对任意的恒成立，则实数 m 的取值范围是　　 A. B. C. D. 10.函数是 R 上的减函数，则实数 a 的取值范围是　　 A. B. C. D. 11.在函数的图象上有一点，此函数与 x 轴、直线及围成图形如图阴影部分的面积 为 S，则 S 与 t 的函数关系图可表示为　　 12 函数 满足 ,且在区间 上 的值域是 ，则坐标 所表示的点在图中的（ ） A． 线段 和线段 上 B． 线段 和线段 上 ( ) 21 4 5f x x x− = + − ( )f x 2 6x x+ 2 8 7x x+ + 2 2 3x x+ − 2 6 10x x+ − )()( xmxxf −= (2 ) ( )f x f x− = [ , ]a b [ 3,1]− ( , )a b AD BC AD DC C． 线段 和线段 上 D． 线段 和线段 上 二、填空题（本大题共 4 小题每题 5 分，共 20 分） 13.设集合 M={a，b，c}，则集合 M 的真子集的个数为______． 14.已知全集 U，集合 ， ，则全集 ． 15.函数 的值域是______________． 16.函数 的单调增区间是 . 三、解答题（解答应写出必要的文字说明和解题步骤，本大题共 6 小题，17 题 10 分，其余每 题各 12 分，共 70 分） 17.（本小题 10 分）已知全集 U=R，A=[-1，3]，B=[-2，2）． （1）求 A∩B，A∪B； （2）求∁U（A∩B），∁U（A∪B）． 18.（本小题 12 分）已知 （1）当 时，求 ； （2）若 ，求实数 的取值范围． 19.（本小题 12 分）已知二次函数 满足 ，且 . （1）求函数 的解析式； （2）令 ，求函数 在 上的最小值. AB DC AC BD { }1,3,5A = { }2,4,6U A = U = 2( ) 6 3, [2,5)f x x x x= − + − ∈ 32)( 2 −−= xxxf { }| 1 3 ,A x x= − < ≤ { }2 2| 1 3B x m x m= ≤ < + 1m = A B B ⊆ RC A m ( )f x ( ) ( )1 2 1f x f x x+ − = − + ( )2 15f = ( )f x ( ) ( ) ( )2 2g x m x f x= − − ( 2)m > ( )g x [ ]0,2x∈ 20.（本小题 12 分）已知函数 f(x)＝Error! (1)求 f(x)的定义域，值域；(2)求 f(f(1))；(3)解不等式 f(x＋1)>1 4. 21. （本小题 12 分）某群体的人均通勤时间，是指单日内该群体中成员从居住地 到工作地的平均用时．某地上班族 S 中的成员仅以自驾或公交方式通勤．分析显 示：当 S 中 x%（0＜x＜100）的成员自驾时，自驾群体的人均通勤时间为 f（x）=（单位：分钟）， 而公交群体的人均通勤时间不受 x 影响，恒为 40 分钟，试根据上述分析结果回答 下列问题： （1）当 x 在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时 间？ （2）求该地上班族 S 的人均通勤时间 g（x）的表达式；讨论 g（x）的单调性， 并说明其实际意义． 22.（本小题 12 分）已知定义在 R 上的函数对任意实数 x，y 都有，且，当时，． 求的值；求证：为 R 上的增函数； 若关于 x 的不等式对任意恒成立，求实数 a 的取值范围． 实验中学 2019-2020 学年上学期高一第一次月考数学试题 命题人：张志明 （考试时间：120 分钟 试卷满分：150 分） 1．设集合 ，集合 ，则集合 ＝(　C　)　 A．{1,3,1,2,4,5} B．{1} C．{1,2,3,4,5} D．{2,3,4,5} http://www.ks5u.com/2．若 且 ，则 （ D ) A．2 B．2 或-2 C．0 或 2 D．0 或 2 或-2 3.设全集 是实数集 ， ， ，则如图所示阴影部分所表示的 集合是（ C ） A． B． C． D． 4.下列集合 A 到 B 的对应中，不能构成映射的是（　A　） B. B. C. D. 5.下列函数中，在区间（0，+∞）上是增函数的是（　A　） A. B. C. D. 6.函数在内递减，在内递增，则 a 的值是　C　 { }3,1=A { }5,4,2,1=B BA  { } { }21,4, , 1,A x B x= = AB ⊆ x = U R { }2>= xxM { }31 <<= xxN { | 2 1}x x− ≤ < { | 2 2}x x− ≤ ≤ { |1 2}x x< ≤ { | 2}x x < U N M A. 1 B. 3 C. 5 D. 【解析】解：依题义可得函数对称轴，． 由题义为二次函数单调性及图象问题，有二次函数在内递减，且在内递增的对称轴方程即可 解出 a 此题重点考查了二次函数的图象及单调性，要求学生熟记二次函数并准确理解二次函数性 质． 7.已知 ，则 的表达式是（ A ） A. B. C. D. 8.函数的图象是　C　 【解析】解：方法 1：图象平移法 将函数的图象向右平移一个单位即可得到函数的图象，所以选 C． 方法 2：利用函数的性质和特殊点的符合判断． 当时，函数无意义，所以排除 B，D． 当时，，所以排除所以选 C． 故选：C． 利用函数图象的平移或者利用函数的性质进行判断即可． 调性，奇偶性，对称性以及特殊点的特殊值进行判断排除，是解决函数图象类题目中最常用 的方法． 9.函数，如果不等式对任意的恒成立，则实数 m 的取值范围是　D　 A. B. C. D. 【答案】D 【解析】解：因为，在上为增函数， 不等式对任意的恒成立， ( ) 21 4 5f x x x− = + − ( )f x 2 6x x+ 2 8 7x x+ + 2 2 3x x+ − 2 6 10x x+ − 所以，对任意的恒成立， 所以对任意的恒成立， 因为在上为增函数，所以， 所以，故选：D． 根据在上为增函数，则不等式对任意的恒成立转化为对任意的恒成立，根据函数的单调性， 求出函数的最值即可． 10.函数是 R 上的减函数，则实数 a 的取值范围是　C　 A. B. C. D. 【解析】解：是 R 上的减函数； ； 解得； 实数 a 的取值范围是． 故选：C． 根据为减函数，以及减函数定义、反比例函数和一次函数单调性即可得出，解该不等式组即 可得出实数 a 的取值范围． 考查减函数的定义，分段函数单调性的判断，以及反比例函数和一次函数的单调性． 11.在函数的图象上有一点，此函数与 x 轴、直线及围成图形如图阴影部分的面积为 S，则 S 与 t 的函数关系图可表示为　B　 【答案】B 【解析】解：由题意知，当时，S 的增长会越来越快， 故函数 S 图象在 y 轴的右侧的切线斜率会逐渐增大， 故选：B． 利用在 y 轴的右侧，S 的增长会越来越快，切线斜率会逐渐增大，从而选出正确的选项． 12 函数 满足 ,且在区间 上 的值域是 ，则坐标 所表示的点在图中的（ B ） A． 线段 和线段 上 B． 线段 和线段 上 C． 线段 和线段 上 D． 线段 和线段 上 13.设集合 M={a，b，c}，则集合 M 的真子集的个数为__7___． 14.已知全集 U，集合 ， ，则全集 ． 15.函数 的值域是______________．(2,6] 16.函数 的单调增区间是 .（3，+∞） 17.已知全集 U=R，A=[-1，3]，B=[-2，2）． （1）求 A∩B，A∪B； （2）求∁U（A∩B），∁U（A∪B）． 【答案】解：（1）∵全集 U=R，A=[-1，3]，B=[-2，2）． ∴A∩B=[-1，3]∩[-2，2）=[-1，2）， A∪B=[-1，3]∪[-2，2]=[-2，3]； （2）∁U（A∩B）=（-∞，-1）∪[2，+∞]， ∁U（A∪B）=（-∞，-2）∪（3，+∞）． 18.已知 （1）当 时，求 ； )()( xmxxf −= (2 ) ( )f x f x− = [ , ]a b [ 3,1]− ( , )a b AD BC AD DC AB DC AC BD { }1,3,5A = { }2,4,6U A = U = { }1,2,3,4,5,6 2( ) 6 3, [2,5)f x x x x= − + − ∈ 32)( 2 −−= xxxf { }| 1 3 ,A x x= − < ≤ { }2 2| 1 3B x m x m= ≤ < + 1m = A B 第 12 题图 （2）若 ，求实数 的取值范围． 【答案】19． (1) ——（4 分） (2) ——（4 分） 19.已知二次函数 满足 ，且 . （1）求函数 的解析式； （2）令 ，求函数 在 上的最小值. 【答案】： （1）设二次函数 （ ），…………1 分 则 ………… 2 分 ∴ ， ，∴ ， …………4 分 又 ，∴ .…………5 分 ∴ …………6 分 （2）∵ ∴ . ， ，对称轴 ， 当 时， ； 20.已知函数 f(x)＝Error! (1)求 f(x)的定义域，值域；(2)求 f(f(1))； (3)解不等式 f(x＋1)>1 4. 【答案】　(1)f(x)的定义域为(0,1)∪[1,2)∪[2，5 2 )＝(0，5 2 ). B ⊆ RC A m { }1 4A B x x= − < < 3 3m m< − >或 ( )f x ( ) ( )1 2 1f x f x x+ − = − + ( )2 15f = ( )f x ( ) ( ) ( )2 2g x m x f x= − − ( 2)m > ( )g x [ ]0,2x∈ ( ) 2f x ax bx c= + + 0a ≠ ( ) ( ) ( ) ( ) ( )2 21 1 1 2 2 1f x f x a x b x c ax bx c ax a b x+ − = + + + + − + + = + + = − + 2 2a = − 1a b+ = 1a = − 2b = ( )2 15f = 15c = ( ) 2 2 15f x x x= − + + ( ) 2 2 15f x x x= − + + ( ) ( ) ( ) 22 2 2 15g x m x f x x mx= − − = − − ( ) 2 2 15g x x mx= − − [ ]0,2x∈ x m= 2m > ( ) ( )min 2 4 4 15 4 11g x g m m= = − − = − − 易知 f(x)在(0,1)上为增函数，在[1，5 2 )上为减函数， ∴当 x＝1 时，f(x)max＝3 4 －1 4 ＝1 2 ，又 f(0)＝0，f(2)＝1 4 ，f (5 2 )＝0， ∴值域为(0，1 2 ]. (2) f(1)＝3 4 －1 4 ＝1 2.f(f(1))＝f (1 2 )＝1 2 1 2 ＝1 4. (3)f(x＋1) >1 4 等价于 Error!①或Error! ②或Error!③ 解①得－1 21 4 的解集为(－1 2，0)∪[0，1 )∪∅＝(－1 2，1). 21.某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时．某地上 班族 S 中的成员仅以自驾或公交方式通勤．分析显示：当 S 中 x%（0＜x＜100）的成员自驾时， 自驾群体的人均通勤时间为 f（x）=（单位：分钟）， 而公交群体的人均通勤时间不受 x 影响，恒为 40 分钟，试根据上述分析结果回答下列问题： （1）当 x 在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？ （2）求该地上班族 S 的人均通勤时间 g（x）的表达式；讨论 g（x）的单调性，并说明其实际 意义． 【答案】解；（1）由题意知，当 30＜x＜100 时， f（x）=2x+-90＞40， 即 x2-65x+900＞0， 解得 x＜20 或 x＞45， ∴x∈（45，100）时，公交群体的人均通勤时间少于自驾群体的人均通勤时间； （2）当 0＜x≤30 时， g（x）=30•x%+40（1-x%）=40-； 当 30＜x＜100 时， g（x）=（2x+-90）•x%+40（1-x%）=-x+58； ∴g（x）=； 当 0＜x＜32.5 时，g（x）单调递减； 当 32.5＜x＜100 时，g（x）单调递增； 说明该地上班族 S 中有小于 32.5%的人自驾时，人均通勤时间是递减的； 有大于 32.5%的人自驾时，人均通勤时间是递增的； 当自驾人数为 32.5%时，人均通勤时间最少． 22.已知定义在 R 上的函数对任意实数 x，y 都有，且，当时，． 求的值； 求证：为 R 上的增函数； 若关于 x 的不等式对任意的恒成立，求实数 a 的取值范围． 【答案】解：令，则有：，即， 再令，，则有：， ， 即： 任取，则， 由题设时，，可得， ， 为 R 上的增函数； 由已知条件有：， 故原不等式可化为：， 即：，又， 故不等式可化为：； 由可知在 R 上为增函数， 所以， 即在上恒成立， 令，则成立即可， 当，即时，在上单调递增， 则， 解得：，又， 所以； 当，即时， 解得：， 而，所以 综上所述：实数 a 的取值范围时．