江苏省苏北四市（徐州、淮安、连云港、宿迁）2020届高三第一次调研考试（期末考试）数学（扫描版） 13页

连云港市 2020 届高三第一学期期末调研考试 数学 I 参考答案与评分标准 一、填空题： 1．{ 1 2 }x x- < < 2． 2i- 3． 4 5 4．20 5．[4,+ )¥ 6． 1 2 7．4 8． 1 4 9．135 10． 3 π2 11． 2 2( 2) 8x y+ + = 12．3 13． 4 7 14． 3 4 二、解答题： 15．（1）在 PBC△ 中，因为 M，N 分别为棱 PB，PC 的中点， 所以 MN// BC． ………………………………3 分 又 MNÌ平面 AMN，BC Ë 平面 AMN， 所以 BC//平面 AMN．…………………………6 分 （2）在 PAB△ 中，因为 AP AB= ，M 为棱 PB 的中点， 所以 AM PB^ ．………………………………8 分 又因为平面 PAB⊥平面 PBC，平面 PAB 平面 PBC PB= ， AM Ì平面 PAB， 所以 AM ^ 平面 PBC．…………………………………………………………12 分 又 AM Ì平面 AMN，所以平面 AMN⊥平面 PBC． …………………………14 分 16．（1）在 ABC△ 中，由余弦定理 2 2 22 cosb c bc A a+ - = 得， 2 520 2 2 5 255b b+ - ´ ´ = ，即 2 4 5 0b b- - = ， …………………………4 分 解得 5b = 或 1b = - （舍），所以 5b = ． ………………………………………6 分 （2）由 5cos 5A = 及 0 A< < p得， 2 25 2 5sin 1 cos 1 ( )5 5A A= - = - = ，…8 分 所以 2 10cos cos( ( )) cos( ) (cos sin )4 2 10C A B A A Ap= p - + = - + = - - = ， 又因为 0 C< < p，所以 2 210 3 10sin 1 cos 1 ( )10 10C C= - = - = ， 从而 3 10 sin 10tan 3cos 10 10 CC C= = = ，………………………………………………12 分 所以 2 2 2tan 2 3 3tan 2 1 tan 1 3 4 CC C ´= = = -- - ．………………………………………14 分 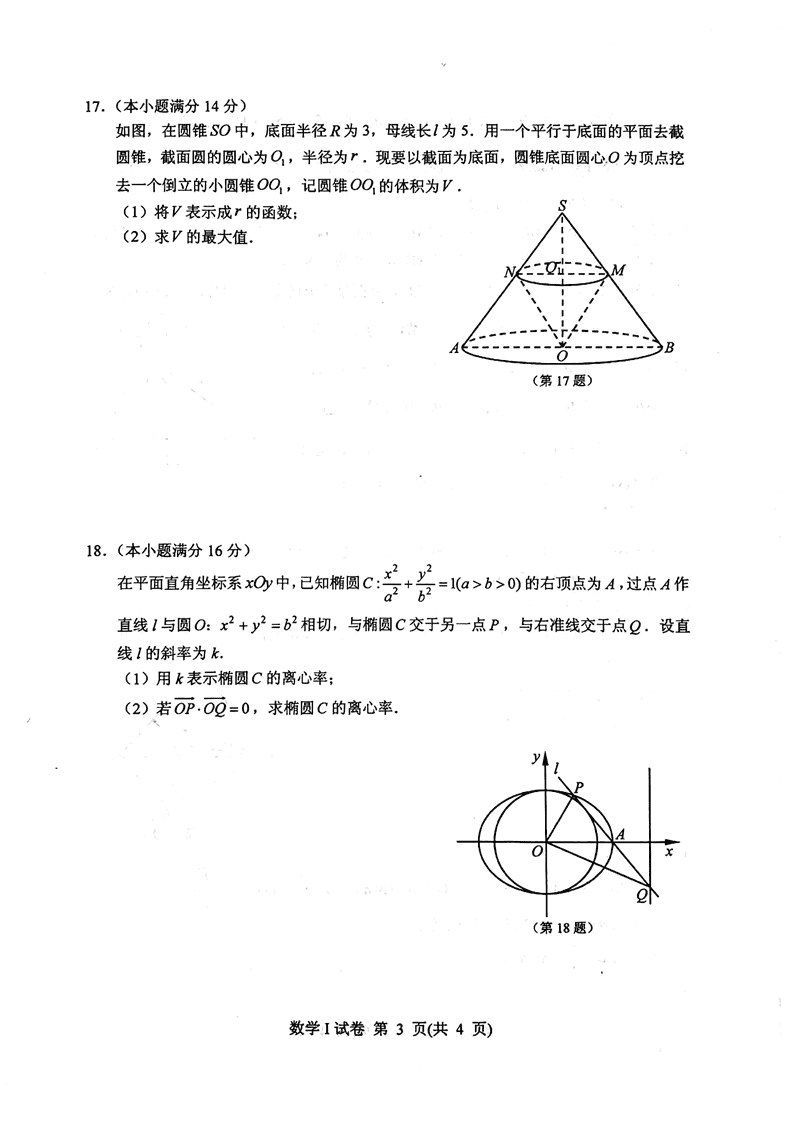17．（1）在 SAO△ 中， 2 2 2 25 3 4SO SA AO= - = - = ， …………………………2 分 A P N M C B 由 1SNO△ ∽ SAO△ 可知， 1SO r SO R= ，所以 1 4 3SO r= ，……………………4 分 所以 1 44 3OO r= - ，所以 2 2 31 4 4( ) π (4 ) π(3 ),0 33 3 9V r r r r r r= - = - < < ．…7 分 （2）由（1）得 2 34( ) π(3 ),0 39V r r r r= - < < ， 所以 24( ) π(6 3 )9V r r r¢ = - ，令 ( ) 0V r¢ = ，得 2r = ，………………………9 分 当 (0,2)rÎ 时， ( ) 0V r¢ > ，所以 ( )V r 在 (0,2) 上单调递增； 当 (2,3)rÎ 时， ( ) 0V r¢ < ，所以 ( )V r 在 (2,3) 上单调递减． 所以当 2r = 时， ( )V r 取得最大值 16π(2) 9V = ． 答：小圆锥的体积V 的最大值为16π 9 ．………………………………………14 分 18．（1）直线 l 的方程为 )( axky -= ，即 0=-- akykx ， 因为直线 l 与圆 222 byxO =+： 相切，所以 b k ak = + - 12 ，故 22 2 2 ba bk - = ． 所以椭圆C 的离心率 2 2 2 11 1 be a k= - = + ．………………………………4 分 （2）设椭圆C 的焦距为 2c ，则右准线方程为 2ax c= ， 由 ïî ïí ì = -= c ax axky 2 )( 得 c acakac aky -=-= 22 )( ，所以 ))(,( 22 c acak c aQ - ，…6 分 由 ïî ïí ì -= =+ )( 12 2 2 2 axky b y a x 得 02)( 2224232222 =-+-+ bakaxkaxkab ， 解得 222 223 kab abkaxp + -= ，则 222 2 222 223 2)( kab kaba kab abkaky p + -=- + -= ， 所以 )2- 222 2 222 223 kab kab kab abkaP ++ - ，（ ，……………………………………………10 分 因为 0=×OQOP ，所以 02)( 222 22 222 2232 = + -×-+ + -× kab kab c acak kab abka c a ， 即 )(2)( 22222 cakbbkaa -=- ，………………………………………………12 分 由（1）知， 22 2 2 ba bk - = ，所以 22 4 2 22 22 )(2)( ba cabb ba baa - -=- - ， 所以 caa 22 -= ，即 ca 2= ，所以 2 1=a c ，故椭圆C 的离心率为 2 1 ．……16 分 19．（1） ( )2 1 1 1( ) lnf x x a x xx ¢ = + - ， 因为曲线 ( )y f x= 在点 (1, (1))f 处的切线方程为 1 0x y+ - = ， 所以 (1) 1 1f a¢ = - = - ，得 0a = ．……………………………………………2 分 （2）因为 2 1 ln( ) ax xf x x - +¢ = 存在两个不相等的零点． 所以 ( ) 1 lng x ax x= - + 存在两个不相等的零点，则 1( )g x ax¢ = + ． ①当 0a≥ 时， ( ) 0g x¢ > ，所以 ( )g x 单调递增，至多有一个零点．……4 分 ②当 0a < 时，因为当 1(0 )x aÎ -， 时， ( ) 0g x¢ > ， ( )g x 单调递增， 当 1( + )x aÎ - ¥， 时， ( ) 0g x¢ < ， ( )g x 单调递减， 所以 1x a= - 时， max 1 1( ) ( ) ln( ) 2g x g a a= - = - - ． …………………………6 分 因为 ( )g x 存在两个零点，所以 1ln( ) 2 0a- - > ，解得 2e 0a-- < < ．………7 分 因为 2e 0a-- < < ，所以 21 e 1a- > > ． 因为 (1) 1 0g a= - < ，所以 ( )g x 在 1(0 )a-， 上存在一个零点． …………8 分 因为 2e 0a-- < < ，所以 21 1( )a a- > - ． 因为 2 21 1 1[( ) ] ln( ) 1g a a a- = - + - ，设 1t a= - ，则 22ln 1( e )y t t t= - - > ， 因为 2 0ty t -¢ = < ，所以 22ln 1( e )y t t t= - - > 单调递减， 所以 ( )2 2 22ln e e 1 3 e 0y < - - = - < ，所以 2 21 1 1[( ) ] ln( ) 1 0g a a a- = - + - < ， 所以 ( )g x 在 1( )a- + ¥， 上存在一个零点． 综上可知，实数 a 的取值范围为 2( e ,0)-- ．…………………………………10 分 （3）当 2a = 时， 1( ) (2 )lnf x xx= - ， ( )2 2 1 1 1 2 1 ln( ) ln 2 x xf x x x xx x - +¢ = + - = ， 设 ( ) 2 1 lng x x x= - + ，则 1( ) 2 0g x x¢ = + > ．所以 ( )g x 单调递增， 且 1 1( ) ln 02 2g = < ， (1) 1 0g = > ，所以存在 0 1( 1)2x Î ， 使得 0( ) 0g x = ，……12 分 因为当 0(0 )x xÎ ， 时， ( ) 0g x < ，即 ( ) 0f x¢ < ，所以 ( )f x 单调递减； 当 0( + )x xÎ ¥， 时， ( ) 0g x > ，即 ( ) 0f x¢ > ，所以 ( )f x 单调递增， 所以 0x x= 时， ( )f x 取得极小值，也是最小值， 此时 ( )0 0 0 0 0 0 0 1 1 1( ) (2 )ln (2 ) 1 2 (4 ) 4f x x x xx x x= - = - - = - + + ，……………14 分 因为 0 1( 1)2x Î ， ，所以 0( ) ( 1 0)f x Î - ， ， 因为 ( )f x l≥ ，且l 为整数，所以 1l -≤ ，即 l 的最大值为 1- ．………16 分 20．（1）由 1 1n na ka+ = - ， 1 3a = 可知， 2 3 1a k= - ， 2 3 3 1a k k= - - ， 因为{ 1}na - 为等比数列，所以 2 2 1 3( 1) ( 1)( 1)a a a- = - - ， 即 2 2(3 2) 2 (3 2)k k k- = ´ - - ，即 23 10 8 0k k- + = ，解得 2k = 或 4 3k = ，…2 分 当 4 3k = 时， 1 43 ( 3)3n na a+ - = - ，所以 3na = ，则 1 2na - = ， 所以数列{ 1}na - 的公比为 1，不符合题意； 当 2k = 时， 1 1 2( 1)n na a+ - = - ，所以数列{ 1}na - 的公比 1 1 21 n n aq a + -= =- ， 所以实数 k 的值为 2 ． …………………………………………………………4 分 （2）由（1）知 1 2n na - = ，所以 4 n n n nb n - ,ìï= í2 ,ïî 为奇数, 为偶数, 则 2 2 (4 1) 4 (4 3) 4 [4 (2 1)] 4m mS m= - + + - + + + - - + 2(4 1) (4 3) [4 (2 1)] 4 4 4mm= - + - + + - - + + + + 14 4(4 ) 3 m m m + -= - + ，……………………………………………………6 分 则 2 1 2 2 4 4(4 ) 3 m m m mS S b m m- -= - = - + ， 因为 2 2 +1 3 2 4m m mb b m+ = - + ，又 2 2 2 +3 2 2 +1( ) ( ) 3 4 2 0m m m m mb b b b+ + - + = ´ - > ， 且 2 3 5 0b b+ = > ， 1 3 0b = > ，所以 2 1 0mS - > ，则 2 0mS > ， 设 2 2 1 0,m t m S b tS - = > Î *N ，…………………………………………………………8 分 则 1,3t = 或t 为偶数，因为 3 1b = 不可能，所以 1t = 或t 为偶数， ①当 2 1 2 1 =m m S bS - 时， 14 4(4 ) 3 34 4(4 ) 3 m m m m m m + -- + =-- + ，化简得 26 24 8 4 4mm m- + = - -≤ ， 即 2 4 2m m- + ≤0 ，所以 m 可取值为 1，2，3， 验证 62 4 1 3 5 7 87, 3,3 23 SS S S S S= = = 得，当 2m = 时， 4 1 3 S bS = 成立．…………………12 分 ②当t 为偶数时， 1 2 2 2 1 4 4(4 ) 33 14 4 3 12 4(4 ) 13 4 m m m m m m mS S m mm m + - -- + = = +- - + -- + + ， 设 23 12 4 4m m m mc - + -= ，则 2 1 1 9 42 21 4m m m m mc c+ + - +- = ， 由①知 3m > ，当 4m = 时， 5 4 5 3 04c c -- = < ； 当 4m > 时， 1 0m mc c+ - > ，所以 4 5 6c c c> < < ，所以 mc 的最小值为 5 19 1024c -= ， 所以 2 2 1 30 1 519 11024 m m S S - < < + <- + ，令 2 2 2 1 4m m S bS - = = ，则 2 31 43 12 4 14m m m+ =- + - + ， 即 23 12 4 0m m- + - = ，无整数解． 综上，正整数 m 的值 2 ．………………………………………………………16 分 数学Ⅱ参考答案与评分标准 21．A．矩阵 M 的特征多项式为 2 3( ) ( 2)( 1) 31f tt ll l ll - -= = - - -- - ．…………2 分 因为矩阵 M 的一个特征值为 4，所以 (4) 6 3 0f t= - = ，所以 2t = ．…………5 分 所以 2 3 2 1 é ù= ê úë û M ，所以 1 1 3 1 3 2 1 3 2 2 1 3 2 4 4 2 2 1 1 2 1 3 2 2 1 3 2 2 2 - -é ù é ù-ê ú ê ú´ - ´ ´ - ´= =ê ú ê ú- -ê ú ê ú´ - ´ ´ - ´ ë ûë û M ．……10 分 B．由 : cos sin 12 0l r q r j+ - = ，及 cosx r q= ， siny r q= ， 所以l 的直角坐标方程为 12 0x y+ - = ． ………………………………………2 分 在曲线C 上取点 ( )2 3 cos 2sinM j j， ，则点 M 到l 的距离 ( ) ( )4sin 12 12 4sin2 3 cos 2sin 12 3 3 2 2 2 d j jj j p p+ - - ++ - = = = ，…………6 分 （第 22 题） B A C x y z B1 A1 C1 当 6j p= 时， d 取最小值 4 2 ，…………………………………………………8 分 此时点 M 的坐标为( )3,1 ．………………………………………………………10 分 C．因为 x y z， ， 都为正数，且 1x y z+ + = ， 所以由柯西不等式得， 1 1 13( )2 2 2x y y z z x+ ++ + + 1 1 1( ) [( 2 ) ( 2 ) ( 2 )]2 2 2 x y y z z xx y y z z x= + + × + + + + ++ + + ………………5 分 21 1 1( 2 2 2 ) 92 2 2x y y z z xx y y z z x× + + × + + × + =+ + +≥ ， 当且仅当 1 3x y z= = = 时等号成立， 所以 1 1 1 2 2 2x y y z z x+ ++ + + 的最小值为 3．…………………………………10 分 22．（1）因为四边形 1 1AA B B 为正方形，所以 1AB BB^ ， 因为平面 1 1AA B B ^平面 1 1BB C C ，平面 1 1AA B B 平面 1 1 1BB C C BB= ， AB Ì 平面 1 1AA B B ，所以 AB ^ 平面 1 1BB C C . ……………………………2 分 以点 B 为坐标原点，分别以 BA , 1BB 所在的直线 为 x , y 轴，建立如图所示的空间直角坐标系 B xyz- . 不妨设正方形 1 1AA B B 的边长为 2， 则 ( )2 0 0A ， ， ， ( )1 0 2 0B ， ， ． 在菱形 1 1BB C C 中，因为 1 1 60BB CÐ = ° ， 所以 1(0 1 3)C ， ， ，所以 1 ( 2 1 3)AC = - ， ， ． 因为平面 1 1AA B B 的法向量为 ( )0 0 1= ， ，n ， 设直线 1AC 与平面 1 1AA B B 所成角为a ， 则 1 | 3 | 6sin |cos , | 42 2 1 ACa = < > = = ´ n ， 即直线 1AC 与平面 1 1AA B B 所成角的正弦值为 6 4 ．………………………6 分 （2）由（1）可知， ( )0 1 3C -， ， ，所以 ( )1 0 2 0CC = ， ， ． 设平面 1ACC 的一个法向量为 ( )1 1 1 1x y z= ， ，n ， 因为 1 1 1 1 0, 0, AC CC ì × =ïí × =ïî n n 即 ( ) ( ) ( ) ( ) 1 1 1 1 1 1 2 1 3 0 0 2 0 0 x y z x y z ì × - =ïí × =ïî ， ， ， ， ， ， ， ， ， 取 1 3 2x = ， 1 0y = ， 1 1z = ，即 1 3 0 12 æ ö= ç ÷è ø ， ，n ． 设平面 1ABC 的一个法向量为 ( )2 2 2 2x y z= ， ，n ， 因为 ( )2 0 0BA = ， ， ， ( )1 0 1 3BC = ， ， ， 所以 ( ) ( ) ( ) ( ) 2 2 2 2 2 2 2 0 0 0 0 1 3 0 x y z x y z × =ìïí × =ïî ， ， ， ， ， ， ， ， ，取 ( )2 0 3 1= -， ，n ．…………8 分 设二面角 1B AC C- - 的平面角为q ， 则 1 2 1 2 1 2 71cos cos 73 1 3 14 q × -= - < >= - = - =× + × + ， n nn n n n ， 所以二面角 1B AC C- - 的余弦值为 7 7 ．…………………………………10 分 23．（1）因为 4n = ，所以 0 4 0 4 2 16C ( ) =3 81a = ， 1 3 1 4 2 32C ( ) =3 27a = ．……………………2 分 （2）当 1 3x = 时， 2 1C ( ) ( )3 3 k k n k k k na x -= ， 又因为 1 1 ! ( 1)!C C!( )! ( 1)!( )! k k n n n nk k n nk n k k n k - - -= = =- - - ，………………………4 分 当 1n = 时， 0 1 1 0 2 2( ) C ( )3 3 n k k k n k a x = - = =å ； …………………………………5 分 当 2n≥ 时， 0 0 2 1( ) ( )C ( ) ( )3 3 n n k k n k k k n k k n k a x n k - = = - = -å å 0 1 2 1 2 1C ( ) ( ) C ( ) ( )3 3 3 3 n n k n k k k n k k n n k k n k- - = = = -å å 1 1 1 2 1 2 1( ) C ( ) ( )3 3 3 3 n n k n k k n k n n - - - = = + - å 1 1 1 1 1 2 1C ( ) ( )3 3 3 n k n k k n k n n - - - - = = - å 11 2 1( )3 3 3 nn n -= - + 2 3 n= ， 当 1n = 时，也符合． 所以 0 ( ) n k k k n k a x = -å 的值为 2 3 n ．………………………………………………10 分