2020学年高一数学下学期期中联考试题（新版）人教版 9页

‎2019学年第二学期期中联考 高一 数学试卷 ‎【完卷时间：120分钟； 满分：150分】‎ 参考公式：1. 样本数据的方差：‎ ‎ ，其中为样本的平均数；‎ ‎ 2. 线性回归方程系数公式：‎ 一、选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写在答题卷上）‎ ‎1、下列所给的运算结果正确的是（ ）‎ A．SQR（4）＝±2 B.5/2＝2.5 C.52＝2.5 D.5 MOD 2＝2.5‎ ‎2．在某次测量中得到的A样本数据如下：82，84，84，86，86，86，88，88，88，88．若B样本数据恰好是A样本数据都加2后所得数据，则A，B两样本的下列数字特征对应相同的是（　 　）‎ A．众数 B．平均数 C．中位数 D．标准差 ‎3.若，，则角的终边在（ ）‎ A. 第一象限 B. 第二象限 C.第三象限 D. 第四象限 ‎4.有5件产品，其中3件正品，2件次品，从中任取2件，则互斥而不对立的两个事件是( )‎ A. 至少有1件次品与至多有1件正品 B. 恰有1件次品与恰有2件正品 C. 至少有1件次品与至少有1件正品 D. 至少有1件次品与都是正品 ‎5. 假设要考察某企业生产的袋装牛奶的质量是否达标,现从500袋牛奶中抽取6袋进行检验,利用随机数表法抽取样本时,先将500袋牛奶按000,001,…,499进行编号,使用下面随机数表中各个5位数组的后3位,选定第7行第5组数开始,取出047作为抽取的代号,继续向右读,随后检验的5袋牛奶的号码是(下面摘取了某随机数表第7行至第9行)(　　)‎ ‎84421　75331　57245　50688　77047　44767　21763‎ ‎35025　83921　20676　63016　47859　16955　56719‎ ‎98105　07185　12867　35807　44395　23879　33211‎ A. 245,331,421,025,016 B. 025,016,105,185,395‎ C. 395,016,245,331,185 D. 447,176,335,025,212‎ ‎6.为了规定工时定额，需要确定加工某种零件所需的时间，为此进行了次试验，得到 - 9 -‎ 组数据：，由最小二乘法求得回归直线方程为．若已知，则（ ）‎ A. B. C. D.‎ ‎7.给出下列命题：‎ ‎①第二象限角大于第一象限角；‎ ‎②三角形的内角是第一象限角或第二象限角；‎ ‎③不论用角度制还是用弧度制度量一个角，它们与扇形所对半径的大小无关；‎ ‎④若，则与的终边相同；‎ ‎⑤若，则是第二或第三象限的角．‎ 其中正确命题的个数是 (　 )‎ A. 1 B. 2 C. 3 D. 4‎ ‎8. 将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的编号为003.这600名学生分住在3个营区,从001到300住在第1营区,从301到495住在第2营区,从496到600住在第3营区,则3个营区被抽中的人数依次为(　　)‎ A. 26,16,8 B. 25,16,9 C. 25,17,8 D. 24,17,9‎ ‎9.把表示成的形式，则使最小的的值是（ ）‎ A． B. C. D.‎ ‎10. 在区间内随机取两个数分别记为,则函数有零点的概率（ ）‎ A. B. C. D. ‎ ‎11．阅读如下程序框图，如果输出，那么空白的判断框中应填人的条件是 （ ）‎ DO ‎ INPUT m LOOP UNTIL m<>0‎ n=1‎ WHILE n<=2019‎ ‎ PRINT “a(n)”;m*n ‎ PRINT “b(n)”;2*m*n ‎ PRINT “r(n)”;abs(m)*n ‎ n=n+1‎ WEND END 第12 题 A．S<8? B．S<12? C．S<14? D．S<16?‎ ‎12．定义：如果一条直线同时与n个圆相切，则称这条直线为这n个圆的公切线。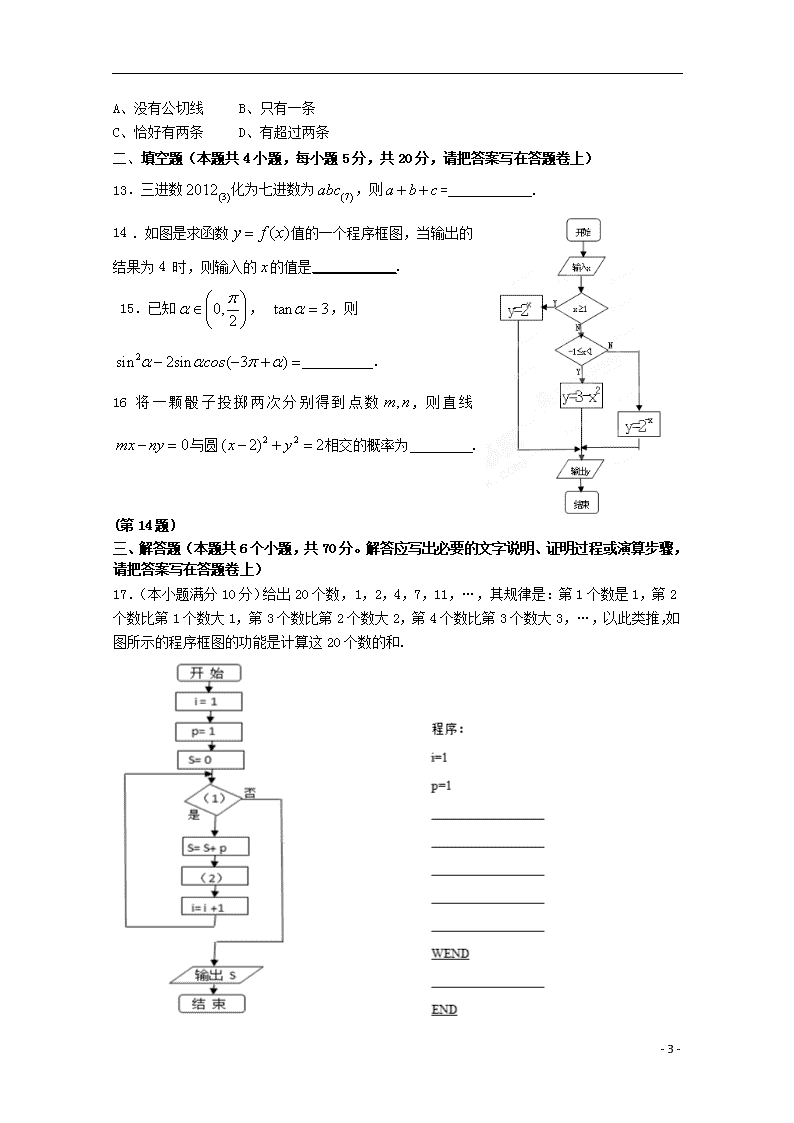已知有2019个圆（n=1,2,3,…,2019）,其中的值由以下程序给出，则这2019个圆的公切线条数（ ）‎ - 9 -‎ A、没有公切线 B、只有一条 C、恰好有两条 D、有超过两条 二、填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上）‎ ‎13．三进数化为七进数为，则=____________.‎ ‎14．如图是求函数值的一个程序框图，当输出的结果为4时，则输入的的值是____________.‎ ‎ 15．已知， ，则__________．‎ ‎16．将一颗骰子投掷两次分别得到点数,则直线与圆相交的概率为 .‎ ‎ ‎ ‎ (第14题) ‎ 三、 解答题（本题共6个小题，共70分。解答应写出必要的文字说明、证明过程或演算步骤，请把答案写在答题卷上）‎ ‎17．（本小题满分10分）给出20个数，1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推，如图所示的程序框图的功能是计算这20个数的和.‎ ‎ ‎ - 9 -‎ ‎(1)请在程序框图中填写两个（_______）内缺少的内容；‎ ‎(2)请补充完整该程序框图对应的计算机程序(用WHILE语句编写).‎ ‎18．（本小题满分12分）‎ ‎（1）用辗转相除法或者更相减损术求和的最大公约数。（写出求解过程）‎ ‎（2）用秦九韶算法写出当时的值。（写出步骤过程）‎ ‎19. （本小题满分12分）已知角的顶点在原点，始边与轴的非负半轴重合，终边在射线上.‎ ‎(1)求的值；‎ ‎(2)求的值.‎ ‎20．（本小题满分12分）某服装批发市场1-5月份的服装销售量x与利润y的统计数据如下表:‎ 月份 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 销售量x(万件)‎ ‎3‎ ‎6‎ ‎4‎ ‎7‎ ‎8‎ 利润y(万元)‎ ‎19‎ ‎34‎ ‎26‎ ‎41‎ ‎46‎ ‎(1)已知销售量x与利润y大致满足线性相关关系,请根据前4个月的数据,求出y 关于x的线性回归方程 ‎(2)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想?‎ - 9 -‎ ‎21．（本小题满分12分）某校高二年级的名学生参加了一次数学测试，已知这名学生的成绩全部介于分到分之间（满分分），为统计学生的这次考试情况，从这名学生中随机抽取名学生的考试成绩作为样本进行统计．将这名学生的测试成绩的统计结果按如下方式分成八组：第一组，第二组，第三组，……，第八组．如图是按上述分组方法得到的频率分布直方图的一部分．‎ ‎（1）求第七组的频率，并完成频率分布直方图；‎ ‎（2）估计该校高二年级的这名学生的这次考试成绩的中位数；‎ ‎（3）若从样本成绩属于第一组和第六组的所有学生中随机抽取 名，求这名学生的分数差的绝对值大于分的概率．‎ ‎22．（本小题满分12分）某中学的高二（1）班女同学有45名，男同学有15名，老师按照分层抽样的方法组建了一个4人的课外兴趣小组。‎ ‎（1）求某同学被抽到的概率及课外兴趣小组中男、女同学的人数；‎ ‎（2）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出1名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名男同学的概率；‎ ‎（3）实验结束后，第一次做实验的同学得到的实验数据为68、70、71、72、74，第二次做实验的同学得到的实验数据为69、70、70、72、74，请问哪位同学的实验更稳定？并说明理由。‎ - 9 -‎ 福州市八县（市）协作校2019学年第二学期期中联考 高一数学参考答案 一、选择题:‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D D B B C A C A B B C 二、填空题:‎ ‎13. 5 14. 2或-2 15. 16. ‎ 三、解答题:‎ ‎17.（本题10分），‎ 第（1）小题（4分）每答对一空得2分，第（2）小题（6分）每答对一空得1分。‎ ‎(1)解： 程序框图的功能是计算这20个数的和，共运算 次，当 时，程序终止，所以第一个条件应填 ，根据第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，可知第二个条件应填.‎ ‎(2)程序，根据程序框图，按顺序主句翻译对应的计算机程序，如下：‎ - 9 -‎ ‎18．（本题12分）‎ ‎（1）（6分）解：‎ 所以459和357的最大公约数是51。‎ 或者 所以459和357的最大公约数是51。‎ ‎（2）（6分）解：‎ 所以 ‎19. （本题12分）‎ - 9 -‎ 解：（1）（6分）由于角终边在射线上，可设终边上一点 ，则， ，…………………………………………………………………………………3分 ‎， ，此时.………………………6分 ‎(2)（6分）‎ ‎ ，… 10分 ‎∵，∴原式.……………………………………………………12分 ‎20．（本题12分）‎ 解：（1）（8分）由前4个月的数据可得， ‎ ‎.…………………………………………………………3分 所以 ，…………………………………5分 ‎，……………………………………………………………………6分 ‎…所以线性回归方程为 ……………………………………………………8分 ‎（2）（4分）由题意得，当时， ， ；………10分 所以利用（2）中的回归方程所得的第5个月的利润估计数据是理想的. …………………………………………………………………………………………12分 ‎21．（本题12分）‎ 解：（1）（4分）由频率分布直方图知第七组的频率 ‎ …………2分 直方图如图． ………………………………………………………………………………4分 ‎（2）（4分）成绩落在第一组的频率为；‎ 成绩落在第二组的频率为；‎ 成绩落在第三组的频率为；‎ 成绩落在第四组的频率为；‎ 由于；‎ 设该校的名学生这次考试成绩的中位数为 - 9 -‎ ‎，则……………………………6分 ‎……………………………………8分 ‎（3）（4分）第六组有学生：人，分别记作；‎ 第一组有学生：人，分别记作．‎ 从中任取人的所有基本事件为 ‎，共个．……………………………………………10分 这名学生的分数差的绝对值大于分，表示所选人来自不同组，其基本事件有个： ‎ 所以从样本成绩属于第一组和第六组的所有学生中随机抽取名，这名学生的分数差的绝对值大于分的概率为：…………………………………………………12分 ‎22. （本题12分）‎ 解：(1)，即每个同学被抽到概率为，…………………………2分 抽到的男同学人数为，被抽到的女同学人数为，所以被抽到的男女同学人数分别为和.……………………………………………………………………4分 ‎(2)把名男同学和名女同学记为、、、，则选取两名同学的基本事件有：，，，，，，，，，，，共12种，其中只有一名男同学的有种，…………………………………………6分 所以。选出恰好只有一名男同学的概率为.……………………………8分 ‎(3)，，，.‎ 综上可知，，所以第二名同学的实验更稳定. ……………………………12分 - 9 -‎