2020版高中数学 第3章 不等式章末分层突破学案 新人教B版必修5 10页

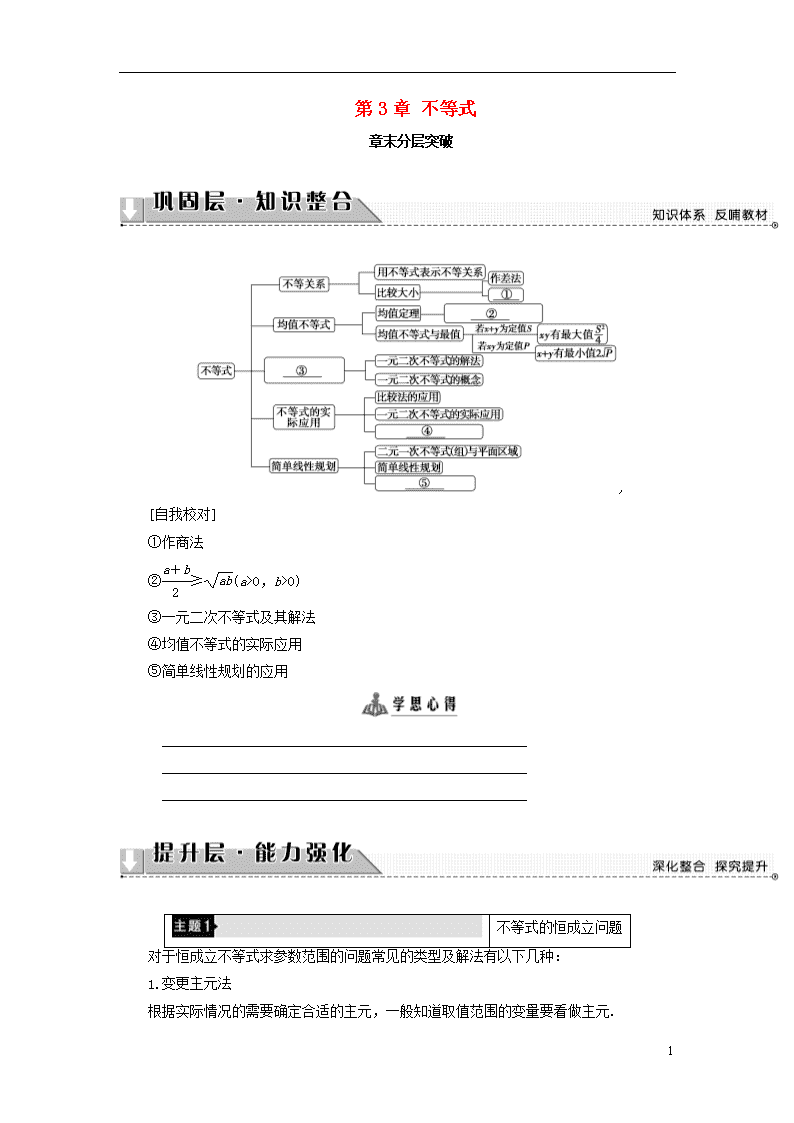
第3章 不等式 章末分层突破 ‎,‎ ‎[自我校对]‎ ‎①作商法 ‎②≥(a>0，b>0)‎ ‎③一元二次不等式及其解法 ‎④均值不等式的实际应用 ‎⑤简单线性规划的应用 ‎　 ‎ ‎　 ‎ ‎　 ‎ 不等式的恒成立问题 对于恒成立不等式求参数范围的问题常见的类型及解法有以下几种：‎ ‎1.变更主元法 根据实际情况的需要确定合适的主元，一般知道取值范围的变量要看做主元.‎ 10‎ ‎2.分离参数法 若f(a)g(x)恒成立，则f(a)>g(x)max.‎ ‎3.数形结合法 利用不等式与函数的关系将恒成立问题通过函数图象直观化.‎ ‎　若不等式x2＋ax＋3－a>0对于满足－2≤x≤2的一切实数 x 恒成立，求实数 a 的取值范围.‎ ‎【精彩点拨】　因为(x－1)的符号不确定，所以参变量 a 不能分离，只好研究二次函数 y＝x2＋ax＋3－a.‎ ‎【规范解答】　设 f(x)＝x2＋ax＋3－a，其函数图象为开口向上的抛物线，要使得对于满足－2≤x≤2的一切实数 x 恒有f(x)>0，只需满足：‎ ‎(1)Δ＝a2－4(3－a)<0；‎ ‎(2) 或 解(1)(2)得，当－70对于满足－2≤x≤2的一切实数x恒成立.‎ ‎[再练一题]‎ ‎1.在R上定义运算：＝ad－bc.若不等式≥1对任意实数 x 恒成立，则实数a的最大值为(　　)‎ A.－　　　B.－　　　C.　　　D. ‎【解析】　原不等式等价于x(x－1)－(a－2)(a＋1)≥1，即x2－x－1≥(a＋1)(a－2)对任意x恒成立，x2－x－1＝2－≥－，所以－≥a2－a－2，‎ ‎－≤a≤.故选D.‎ ‎【答案】　D 利用均值不等式求最值 均值不等式是证明不等式、求某些函数的最大值及最小值的理论依据，在解决数学问题和实际问题中应用广泛.‎ ‎(1)均值不等式通常用来求最值，一般用a＋b≥2(a>0，b>0)解“定积求和，和最小”问题，用ab≤2解“定和求积，积最大”问题.‎ ‎(2)在实际运用中，经常涉及函数f(x)＝x＋(k 10‎ ‎>0)，一定要注意适用的范围和条件：“一正、二定、三相等”.特别是利用拆项、添项、配凑、分离变量、减少变元等，构造定值条件的方法和对等号能否成立的验证.‎ ‎　设函数 f(x)＝x＋，x∈.‎ ‎(1)当a＝2时，求函数 f (x) 的最小值；‎ ‎(2)当00，>0，‎ ‎∴x＋1＋≥2，当且仅当x＋1＝，‎ 即x＝－1时， f (x) 取最小值，此时f (x) min＝‎ ‎2－1.‎ ‎(2)当00，Δ＝0，Δ<0三种情况并加以讨论.‎ ‎(3)若含参数的一元二次不等式可以转化成用其根x1，x2表示的形如a(x－x1)(x－x2)的形式时，往往需要对其根分x1>x2，x1＝x2，x10，得x<－1或x>2.‎ 对于方程2x2＋(2k＋5)x＋5k＝0有两个实数解 x1＝－，x2＝－k.‎ ‎(1)当－>－k，即k>时，不等式的解集为 ，显然－2∉.‎ ‎(2) 当－k＝－时，不等式2x2＋(2k＋5)x＋5k<0的解集为∅.‎ ‎(3)当－<－k，即k<时，‎ 不等式的解集为.‎ ‎∴不等式组的解集由 或确定.‎ ‎∵原不等式组整数解只有－2，‎ ‎∴－2<－k≤3，‎ 故所求k的范围是－3≤k<2.‎ ‎[再练一题]‎ ‎5.解不等式>1(a≠1).‎ ‎【解】　原不等式可化为－1>0，‎ 即(a－1)(x－2)>0(*)，‎ ‎(1)当a>1时，(*)式即为(x－2)>0，而－2＝<0，所以<2，此时x>2或x<.‎ ‎(2)当a<1时，(*)式即为(x－2)<0，而2－＝，‎ ‎①若02，此时20且a≠1，b≠1，若logab>1，则(　　)‎ A.(a－1)(b－1)<0 B.(a－1)(a－b)>0‎ C.(b－1)(b－a)<0 D.(b－1)(b－a)>0‎ ‎【解析】　∵a，b>0且a≠1，b≠1，∴当a>1，即a－1>0时，不等式logab>1可化为alogab>a1，即b>a>1，‎ ‎∴(a－1)(a－b)<0，(b－1)(a－1)>0，(b－1)(b－a)>0.‎ 当01可化为alogab0，(b－1)(b－a)>0.综上可知，选D.‎ ‎【答案】　D ‎2.在平面上，过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在直线x＋y－2＝0上的投影构成的线段记为AB，则|AB|＝(　　)‎ A.2 B.4‎ C.3 D.6‎ ‎【解析】　作出可行域，如图所示.‎ 由 得A′(2，－2).‎ 由 得B′(－1,1).‎ 由于直线x＋y＝0与直线x＋y－2＝0平行，所以可行域中的点在直线x＋y－2＝0上的投影AB的长度|AB|＝|A′B′|＝＝3.‎ ‎【答案】　C ‎3.若log4(‎3a＋4b)＝log2，则a＋b的最小值是(　　)‎ A.6＋2 B.7＋2 C.6＋4 D.7＋4 10‎ ‎【解析】　由题意得 所以 又log4(‎3a＋4b)＝log2，‎ 所以log4(‎3a＋4b)＝log4ab，‎ 所以‎3a＋4b＝ab，故＋＝1.‎ 所以a＋b＝(a＋b)＝7＋＋≥7＋2＝7＋4，当且仅当＝时取等号.故选D.‎ ‎【答案】　D ‎4.函数y＝的定义域是________.‎ ‎【解析】　要使函数有意义，需3－2x－x2≥0，即x2＋2x－3≤0，得(x－1)(x＋3)≤0，即－3≤x≤1，故所求函数的定义域为[－3,1].‎ ‎【答案】　[－3,1]‎ ‎5.某化肥厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示：‎ ‎　　原料 肥料　　‎ A B C 甲 ‎4‎ ‎8‎ ‎3‎ 乙 ‎5‎ ‎5‎ ‎10‎ 现有A种原料200吨，B种原料360吨，C种原料300吨.在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元.分别用x，y表示计划生产甲、乙两种肥料的车皮数.‎ ‎(1)用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；‎ ‎(2)问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润.‎ ‎【解】　(1)由已知，x，y满足的数学关系式为 该二元一次不等式组所表示的平面区域为图①中的阴影部分.‎ 10‎ ‎(2)设利润为z万元，则目标函数为z＝2x＋3y.‎ 考虑z＝2x＋3y，将它变形为y＝－x＋，它的图象是斜率为－，随z变化的一族平行直线，为直线在y轴上的截距，当取最大值时，z的值最大.根据x，y满足的约束条件，由图②可知，当直线z＝2x＋3y经过可行域上的点M时，截距最大，即z最大.‎ 解方程组得点M的坐标为(20,24)，‎ 所以zmax＝2×20＋3×24＝112.‎ 答：生产甲种肥料20车皮，乙种肥料24车皮时利润最大，且最大利润为112万元.‎ 10‎