高考数学二轮复习教案：基础保分强化训练(三) 6页

基础保分强化训练(三)‎ ‎1．已知＝(1＋i)2(i为虚数单位)，则复数z的共轭复数为(　　)‎ A．－－i B．－＋i C.－i D.＋i 答案　B 解析　∵＝(1＋i)2，∴z＝＝＝＝－－i，∴＝－＋i.故选B.‎ ‎2．设命题p：∀x∈R，x3－x2＋1≤0，则p为(　　)‎ A．∃x∈R，x3－x2＋1>0 B．∀x∈R，x3－x2＋1>0‎ C．∃x∈R，x3－x2＋1≤0 D．∀x∈R，x3－x2＋1≥0‎ 答案　A 解析　∵命题p：∀x∈R，x3－x2＋1≤0，∴p为∃x∈R，x3－x2＋1>0.故选A.‎ ‎3．已知集合A＝{x∈Z|x2－4x<0}，B＝{x∈Z|02时，得到函数y＝log2x.‎ 因此，若输出的结果为1时，‎ ‎①若x≤2，得到x2－1＝1，解得x＝±；‎ ‎②若x>2，得到log2x＝1，解得x＝2(舍去)．‎ 因此，可输入的实数x的值可能为－，，共有2个．故选B.‎ ‎5．已知函数f(x)＝cos(x＋θ)(0<θ<π)在x＝时取得最小值，则f(x)在[0，π]上的单调递增区间是(　　)‎ A. B. C. D. 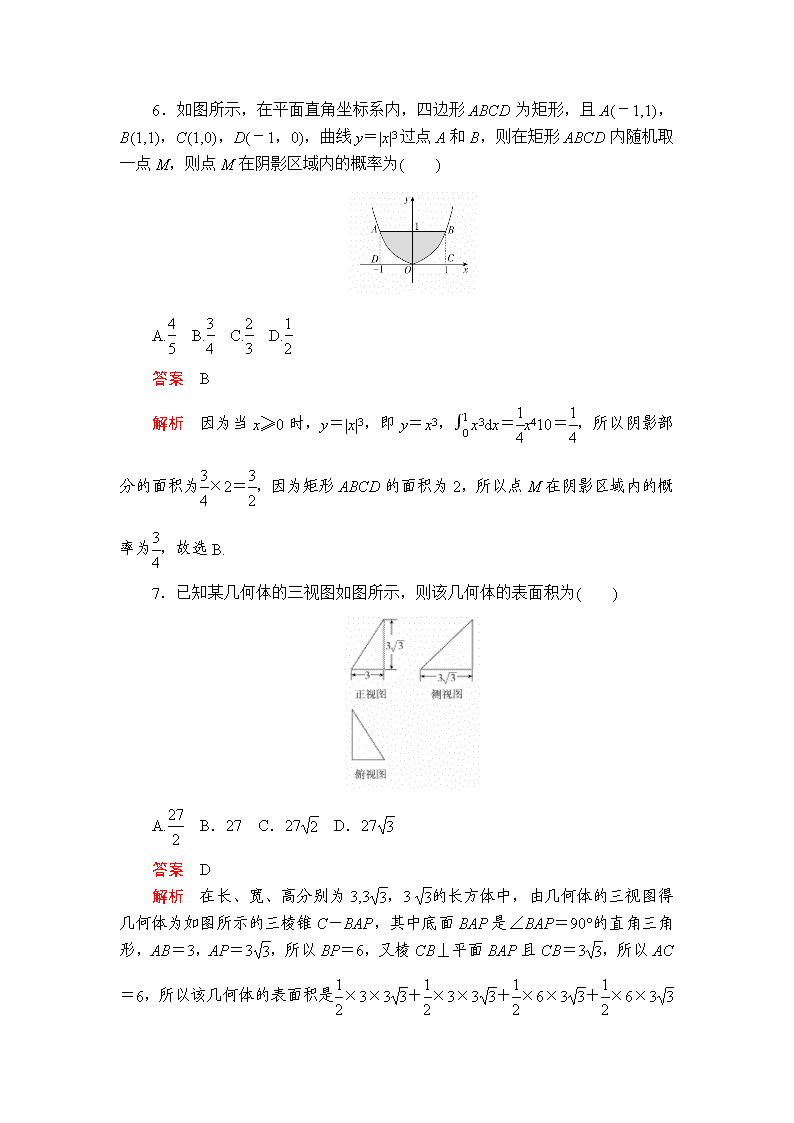答案　A 解析　因为0<θ<π，所以<＋θ<，又f(x)＝cos(x＋θ)在x＝时取得最小值，所以＋θ＝π，θ＝，所以f(x)＝cos.由0≤x≤π，得≤x＋≤.由π≤x＋≤，得≤x≤π，所以f(x)在[0，π]上的单调递增区间是，故选A.‎ ‎6．如图所示，在平面直角坐标系内，四边形ABCD为矩形，且A(－1,1)，B(1,1)，C(1,0)，D(－1，0)，曲线y＝|x|3过点A和B，则在矩形ABCD内随机取一点M，则点M在阴影区域内的概率为(　　)‎ A. B. C. D. 答案　B 解析　因为当x≥0时，y＝|x|3，即y＝x3，x3dx＝x410＝，所以阴影部分的面积为×2＝，因为矩形ABCD的面积为2，所以点M在阴影区域内的概率为，故选B.‎ ‎7．已知某几何体的三视图如图所示，则该几何体的表面积为(　　)‎ A. B．27 C．27 D．27 答案　D 解析　在长、宽、高分别为3,3，3的长方体中，由几何体的三视图得几何体为如图所示的三棱锥C－BAP，其中底面BAP是∠BAP＝90°的直角三角形，AB＝3，AP＝3，所以BP＝6，又棱CB⊥平面BAP且CB＝3，所以AC＝6，所以该几何体的表面积是×3×3＋×3×3＋×6×3＋×6×3＝27，故选D.‎ ‎8．已知抛物线C：y2＝2px(p>0)的焦点为F，过F且倾斜角为120°的直线与抛物线C交于A，B两点，若AF，BF的中点在y轴上的射影分别为M，N，且|MN|＝4，则抛物线C的准线方程为(　　)‎ A．x＝－1 B．x＝－2 C．x＝－ D．x＝－3‎ 答案　D 解析　设AF，FB的中点分别为D，E，则|AB|＝2|DE|，由题得|DE|＝ ‎＝8，所以|AB|＝16，设A(x1，y1)，B(x2，y2)，则x1＋x2＋p＝16，∴x1＋x2＝16－p，联立直线和抛物线的方程得∴3x2－5px＋p2＝0，所以16－p＝，∴p＝6，所以抛物线的准线方程为x＝－3.故选D.‎ ‎9．在△ABC中，D为三角形所在平面内一点，且＝＋，则＝(　　)‎ A. B. C. D. 答案　B 解析　如图，由题意可知，点D在平行于AB边的中位线EF上且满足DE＝AB，S△ABD＝S△ABC，S△ACD＝S△ABC，∴S△BCD＝S△ABC＝S△ABC，∴＝，故选B.‎ ‎10．如图，为了测量某湿地A，B两点间的距离，观察者找到在同一直线上的三点C，D，E.从D点测得∠ADC＝67.5°，从C点测得∠ACD＝45°，∠BCE＝75°，从E点测得∠BEC＝60°.若测得DC＝2，CE＝(单位：百米)，则A，B两点间的距离为(　　)‎ A. B．2 C．3 D．2 答案　C 解析　根据题意，在△ADC中，∠ACD＝45°，∠ADC＝67.5°，DC＝2，则∠DAC＝180°－45°－67.5°＝67.5°，则AC＝DC＝2，在△BCE中，∠BCE＝75°，∠BEC＝60°，CE＝，则∠EBC＝180°－75°－60°＝45°，则有＝，变形可得BC＝＝＝，在△ABC中，AC＝2，BC＝‎ ，∠ACB＝180°－∠ACD－∠BCE＝60°，则AB2＝AC2＋BC2－2AC·BC·cos∠ACB＝9，则AB＝3.故选C.‎ ‎11．已知直线l与曲线y＝x3－6x2＋13x－9相交，交点依次为A，B，C，且|AB|＝|BC|＝，则直线l的方程为(　　)‎ A．y＝－2x＋3 B．y＝2x－3‎ C．y＝3x－5 D．y＝－3x＋2‎ 答案　B 解析　设f(x)＝x3－6x2＋13x－9，则f′(x)＝3x2－12x＋13，设g(x)＝3x2－12x＋13，则g′(x)＝6x－12，令g′(x)＝0，得x＝2，所以曲线y＝x3－6x2＋13x－9的对称中心为(2,1)．由|AB|＝|BC|可知直线l经过点(2,1)，由解得或因此可得直线l过点(1，－1)，(3,3)，(2,1)，所以直线l的方程为y＝2x－3.故选B.‎ 答案　1‎ 解析　由二项式定理的展开式可得Cx10－rr ‎13．已知圆C：(x－3)2＋(y－4)2＝1和两点A(－m,0)，B(m,0)(m>0)，若圆上存在点P，使得∠APB＝90°，则m的取值范围是________．‎ 答案　[4,6]‎ 解析　由已知，以AB为直径的圆与圆C有公共点，又AB的中点为原点，则|AB|＝2m，则|m－1|≤≤m＋1，解得4≤m≤6，即m的取值范围是[4,6]．‎ ‎14．已知四棱锥P－ABCD的底面为矩形，平面PBC⊥平面ABCD，PE⊥BC于点E，EC＝1，AB＝，BC＝3，PE＝2，则四棱锥P－ABCD 的外接球半径为________．‎ 答案　2‎ 解析　如图，由已知，设三角形PBC外接圆圆心为O1，由正弦定理可求出三角形PBC外接圆半径为，设F为BC边的中点，进而求出O1F＝，设四棱锥的外接球球心为O，外接球半径的平方为2＋O1F2＝4，所以四棱锥外接球半径为2.‎