高中数学人教a版选修4-1学业分层测评7圆内接四边形的性质与判定定理word版含解析 8页

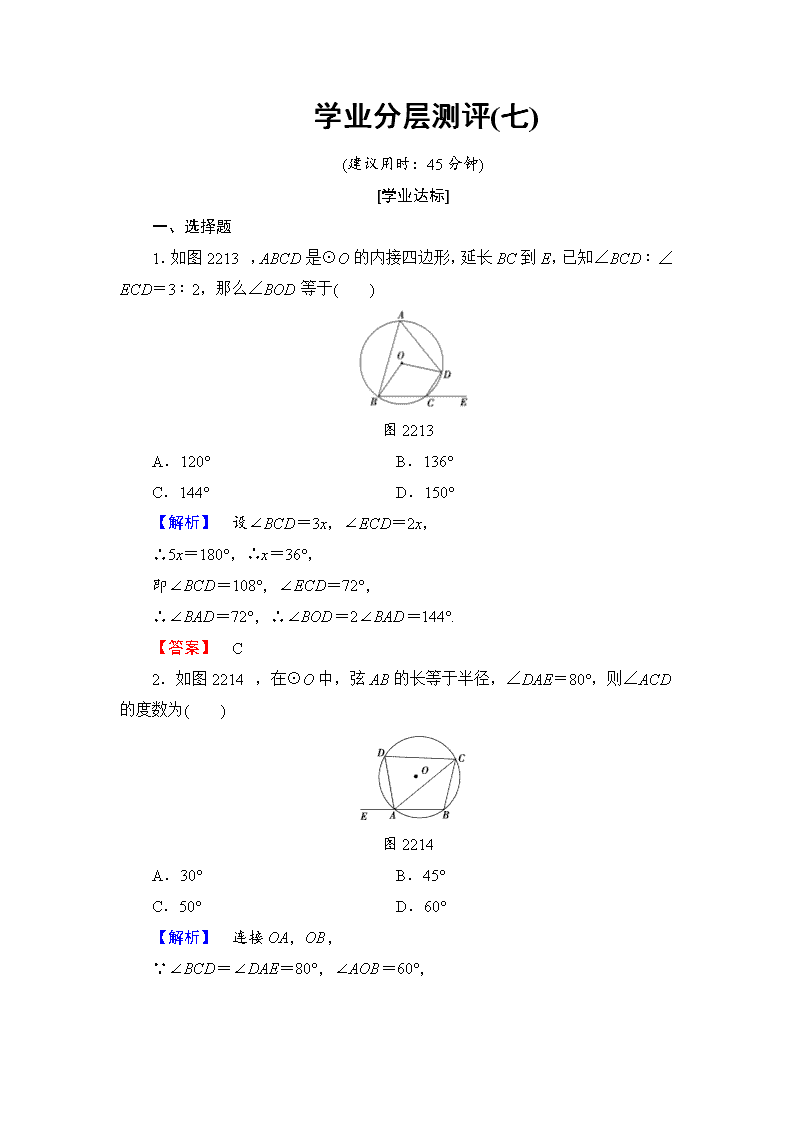
学业分层测评(七) (建议用时：45 分钟) [学业达标] 一、选择题 1．如图 2213，ABCD 是⊙O 的内接四边形，延长 BC 到 E，已知∠BCD∶ ∠ECD＝3∶2，那么∠BOD 等于( ) 图 2213 A．120° B．136° C．144° D．150° 【解析】 设∠BCD＝3x，∠ECD＝2x， ∴5x＝180°，∴x＝36°， 即∠BCD＝108°，∠ECD＝72°， ∴∠BAD＝72°，∴∠BOD＝2∠BAD＝144°. 【答案】 C 2．如图 2214，在⊙O 中，弦 AB 的长等于半径，∠DAE＝80°，则∠ACD 的度数为( ) 图 2214 A．30° B．45° C．50° D．60° 【解析】 连接 OA，OB， ∵∠BCD＝∠DAE＝80°，∠AOB＝60°， ∴∠BCA＝1 2 ∠AOB＝30°， ∴∠ACD＝∠BCD－∠BCA＝80°－30°＝50°. 【答案】 C 3．圆内接四边形 ABCD 中，∠A∶∠B∶∠C∶∠D 可以是( ) A．4∶2∶3∶1 B．4∶3∶1∶2 C．4∶1∶3∶2 D．以上都不对 【解析】 由四边形 ABCD 内接于圆，得∠A＋∠C＝∠B＋∠D，从而只有 B 符合题意． 【答案】 B 4．如图 2215，四边形 ABCD 为圆内接四边形，AC 为 BD 的垂直平分线， ∠ACB＝60°，AB＝a，则 CD 等于( ) 图 2215 A. 3 3 a B. 6 2 a C.1 2a D.1 3a 【解析】 ∵AC 为 BD 的垂直平分线， ∴AB＝AD＝a，AC⊥BD. ∵∠ACB＝60°，∴∠ADB＝60°， ∴AB＝AD＝BD，∴∠ACD＝∠ABD＝60°， ∴∠CDB＝30°， ∴∠ADC＝90°，∴CD＝tan 30°·AD＝ 3 3 a. 【答案】 A 5．如图 2216 所示，圆内接四边形 ABCD 的一组对边 AD，BC 的延长线相 交于点 P，对角线 AC 和 BD 相交于点 Q，则图中共有相似三角形的对数为( ) 【导学号：07370035】 图 2216 A．4 B．3 C．2 D．1 【解析】 利用圆周角和圆内接四边形的性质定理，可得△PCD∽△PAB， △QCD∽△QBA，△AQD∽△BQC，△PAC∽△PBD.因此共 4 对． 【答案】 A 二、填空题 6．如图 2217，以 AB＝4 为直径的圆与△ABC 的两边分别交于 E，F 两点， ∠ACB＝60°，则 EF＝________. 图 2217 【解析】 如图，连接 AE. ∵AB 为圆的直径， ∴∠AEB＝∠AEC＝90°. ∵∠ACB＝60°， ∴∠CAE＝30°， ∴CE＝1 2AC. ∵∠C＝∠C，∠CFE＝∠B， ∴△CFE∽△CBA， ∴EF AB ＝CE AC ， ∵AB＝4，CE＝1 2AC，∴EF＝2. 【答案】 2 7．四边形 ABCD 内接于⊙O，BC 是直径， ＝40°，则∠D＝__________. 【解析】 如图，连接 AC.∵ ＝40°.BC 是⊙O 的直径， ∴∠ACB＝20°，∠BAC＝90°， ∴∠B＝180°－∠BAC－∠ACB＝70°， ∴∠D＝180°－∠B＝110°. 【答案】 110° 8．如图 2218，四边形 ABCD 是圆 O 的内接四边形，延长 AB 和 DC 相交 于点 P，若PB PA ＝1 2 ，PC PD ＝1 3 ，则BC AD 的值为________． 图 2218 【解析】 由于∠PBC＝∠PDA，∠P＝∠P， 则△PAD∽△PCB ，∴PC PA ＝PB PD ＝BC AD. 又PB PA ＝1 2 ，PC PD ＝1 3 ，∴PB PA ×PC PD ＝1 2 ×1 3 ， ∴PC PA ×PB PD ＝1 6 ，∴BC AD ×BC AD ＝1 6 ， ∴BC AD ＝ 6 6 . 【答案】 6 6 三、解答题 9．如图 2219，A，B，C，D 四点在同一圆上，AD 的延长线与 BC 的延长 线交于 E 点，且 EC＝ED. 图 2219 (1)证明：CD∥AB； (2)延长 CD 到 F，延长 DC 到 G，使得 EF＝EG，证明：A，B，G，F 四点 共圆． 【证明】 (1)因为 EC＝ED，所以∠EDC＝∠ECD. 因为 A，B，C，D 四点在同一圆上， 所以∠EDC＝∠EBA， 故∠ECD＝∠EBA，所以 CD∥A B. (2)由(1)知，AE＝BE，∠EDF＝∠ECG，因为 EF＝EG，故∠EFD＝∠EGC， 从而∠FED＝∠GEC. 连接 AF，BG，则△EFA≌△EGB，故∠FAE＝∠GBE. 又 CD∥AB，∠EDC＝∠ECD， 所以∠FAB＝∠GBA，所以∠AFG＋∠GBA＝180°. 故 A，B，G，F 四点共圆． 10．如图 2220，已知 P 为正方形 ABCD 的对角线 BD 上一点，通过 P 作正 方形的边的垂线，垂足分别为 E，F，G，H.你能判断出 E，F，G，H 是否在同 一个圆上吗？试说明你的猜想． 【导学号：07370036】 图 2220 【解】 猜想：E，F，G，H 四个点在以 O 为圆心的圆上．证明如下： 如图，连接 OE，OF，OG，OH. 在△OBE，△OBF，△OCG，△OAH 中， OB＝OC＝OA. ∵PEBF 为正方形， ∴BE＝BF＝CG＝AH， ∠OBE＝∠OBF＝∠OCG＝∠OAH＝45°. ∴△OBE≌△OBF≌△OCG≌△OAH. ∴OE＝OF＝OG＝OH. 由圆的定义可知：E，F，G，H 在以 O 为圆心的圆上． [能力提升] 1．已知四边形 ABCD 是圆内接四边形，下列结论中正确的有( ) ①如果∠A＝∠C，则∠A＝90°； ②如果∠A＝∠B，则四边形 ABCD 是等腰梯形； ③∠A 的外角与∠C 的外角互补； ④∠A∶∠B∶∠C∶∠D 可以是 1∶2∶3∶4. A．1 个 B．2 个 C．3 个 D．4 个 【解析】 由“圆内接四边形的对角互补”可知：①相等且互补的两角必为 直角；②两相等邻角的对角也相等(亦可能有∠A＝∠B＝∠C＝∠D 的特例)；③ 互补两内角的外角也互补；④两组对角之和的份额必须相等(这里 1＋3≠2＋4)．因 此得出①③正确，②④错误． 【答案】 B 2．如图 2221，以△ABC 的一边 AB 为直径的圆交 AC 边于 D，交 BC 边于 E，连接 DE，BD 与 AE 交于点 F.则 sin∠CAE 的值为( ) 图 2221 A.DF AD B.CD AC C.EF AF D.DE AB 【解析】 根据圆周角定理，易得∠AEB＝90°，进而可得∠AEC＝90°. 在 Rt△AEC 中，由锐角三角函数的定义，可得 sin∠CAE＝CE AC ，由圆内接四 边形的性质，可得∠CED＝∠CAB，∠CDE＝∠CBA，可得△CDE∽△CBA，则 有CE AC ＝DE AB ，故有 sin∠CAE＝DE AB. 【答案】 D 3．如图 2222，AB＝10 cm，BC＝8 cm，CD 平分∠ACB，则 AC＝__________， BD＝__________. 图 2222 【解析】 ∠ACB＝90°，∠ADB＝90°. 在 Rt△ABC 中，AB＝10，BC＝8， ∴AC＝ AB2－BC2＝6. 又∵CD 平分∠ACB， 即∠ACD＝∠BCD， ∴AD＝BD， ∴BD＝ AB2 2 ＝5 2. 【答案】 6 5 2 4.如图 2223，锐角△ABC 的内心为 I，过点 A 作直线 BI 的垂线，垂足为 H， 点 E 为内切圆 I 与边 CA 的切点． 图 2223 (1)求证：四点 A，I，H，E 共圆； (2)若∠C＝50°，求∠IEH 的度数． 【解】 (1)证明：由圆 I 与边 AC 相切于点 E， 得 IE⊥AE， 结合 IH⊥AH，得∠AEI＝∠AHI＝90°. 所以四点 A，I，H，E 共圆． (2)由(1)知四点 A，I，H，E 共圆，得∠IEH＝∠HAI. 在△HIA 中，∠HIA＝∠ABI＋∠BAI＝1 2 ∠B＋1 2 ∠A＝1 2(∠B＋∠A) ＝1 2(180°－∠C)＝90°－1 2 ∠C. 结合 IH⊥AH，得∠HAI＝90°－∠HIA＝1 2 ∠C， 所以∠IEH＝1 2 ∠C. 由∠C＝50°，得∠IEH＝25°.