高考数学专题复习教案： 同角三角函数的基本关系式与诱导公式备考策略 3页

同角三角函数的基本关系式与诱导公式备考策略 主标题：同角三角函数的基本关系式与诱导公式备考策略 副标题：通过考点分析高考命题方向，把握高考规律，为学生备考复习打通快速通道。‎ 关键词：平方关系，商的关系，备考策略 难度：2‎ 重要程度：4‎ 内容 考点一　同角三角函数基本关系式的应用 ‎【例1】 (1)已知tan α＝2，则＝___________，‎ ‎4sin2 α－3sin αcos α－5cos2α＝________.‎ ‎(2)(2014·山东省实验中学诊断)已知sin θ·cos θ＝，且＜θ＜，则cos θ－sin θ的值为________．‎ 解析　(1)＝＝＝－1，‎ ‎4sin2 α－3sin αcos α－5cos2α＝ ‎＝＝＝1.‎ ‎(2)当＜θ＜时，sin θ＞cos θ，‎ ‎∴cos θ－sin θ＜0，‎ 又(cos θ－sin θ)2＝1－2sin θcos θ＝1－＝，‎ ‎∴cos θ－sin θ＝－.‎ 答案　(1)－1　1　(2)－ ‎【备考策略】(1)应用公式时注意方程思想的应用，对于sin α＋cos α，sin α－cos α，sin αcos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α可以知一求二．‎ ‎(2)关于sin α，cos α的齐次式，往往化为关于tan α的式子．‎ 考点二　利用诱导公式化简三角函数式 ‎【例2】 (1)sin(－1 200°)cos 1 290°＋cos(－1 020°)·sin(－1 050°)＝________.‎ ‎(2)设f(α)＝(1＋2sin α≠0)，则f＝________.‎ 解析　(1)原式＝－sin 1 200°cos 1 290°－cos 1 020°sin1 050°‎ ‎＝－sin(3×360°＋120°)cos(3×360°＋210°)－cos(2×360°＋300°)sin(2×360°＋330°)‎ ‎＝－sin 120°cos 210°－cos 300°sin 330°‎ ‎＝－sin(180°－60°)cos(180°＋30°)－cos(360°－60°)·sin(360°－30°)‎ ‎＝sin 60°cos 30°＋cos 60°sin 30°＝×＋×＝1.‎ ‎(2)∵f(α)＝ ‎＝＝＝，‎ ‎∴f＝＝ ‎＝＝.‎ 答案　(1)1　(2) ‎【备考策略】 (1)诱导公式应用的原则：负化正、大化小，化到锐角为终了．‎ ‎(2)诱导公式应用的步骤：‎ 任意负角的三角函数→任意正角的三角函数→‎ ‎0～2π的角的三角函数→锐角三角函数 注意：诱导公式应用时不要忽略了角的范围和三角函数的符号．‎ 考点三　利用诱导公式求值 ‎【例3】 (1)已知sin＝，则cos＝______；‎ ‎(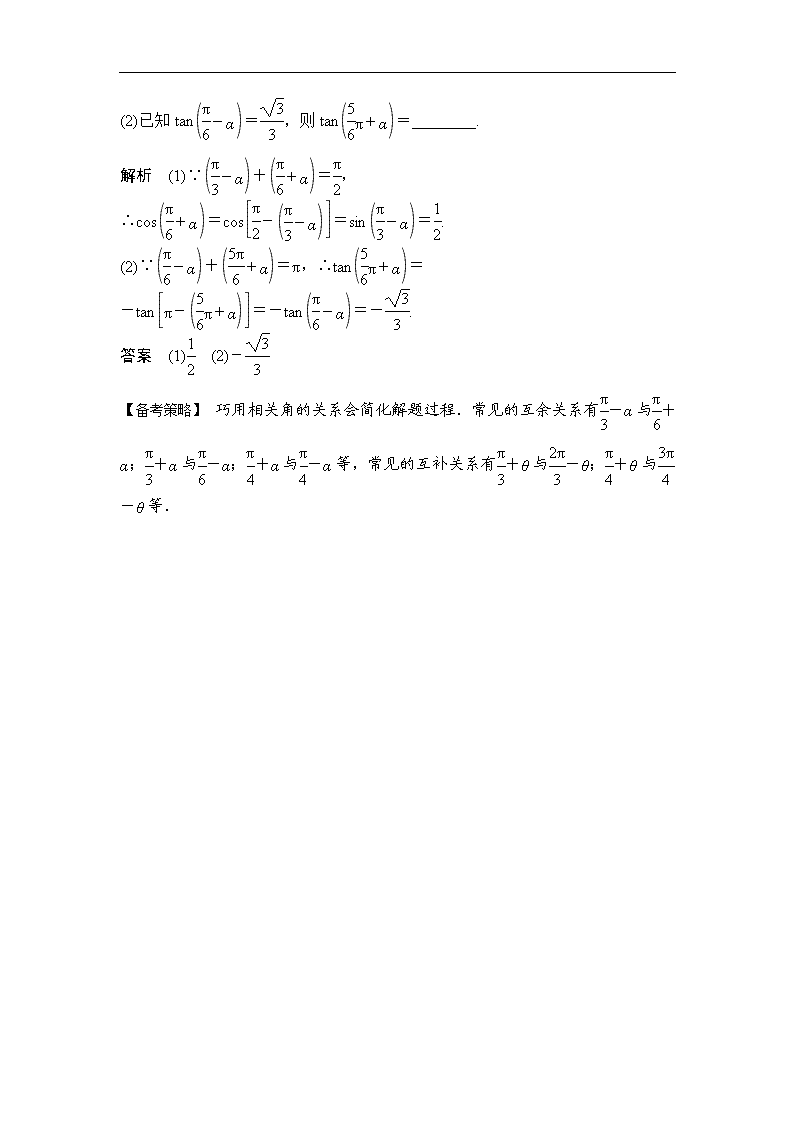2)已知tan＝，则tan＝________.‎ 解析　(1)∵＋＝，‎ ‎∴cos＝cos＝sin＝.‎ ‎(2)∵＋＝π，∴tan＝‎ ‎－tan＝－tan＝－.‎ 答案　(1)　(2)－ ‎【备考策略】 巧用相关角的关系会简化解题过程．常见的互余关系有－α与＋α；＋α与－α；＋α与－α等，常见的互补关系有＋θ与－θ；＋θ与－θ等．‎