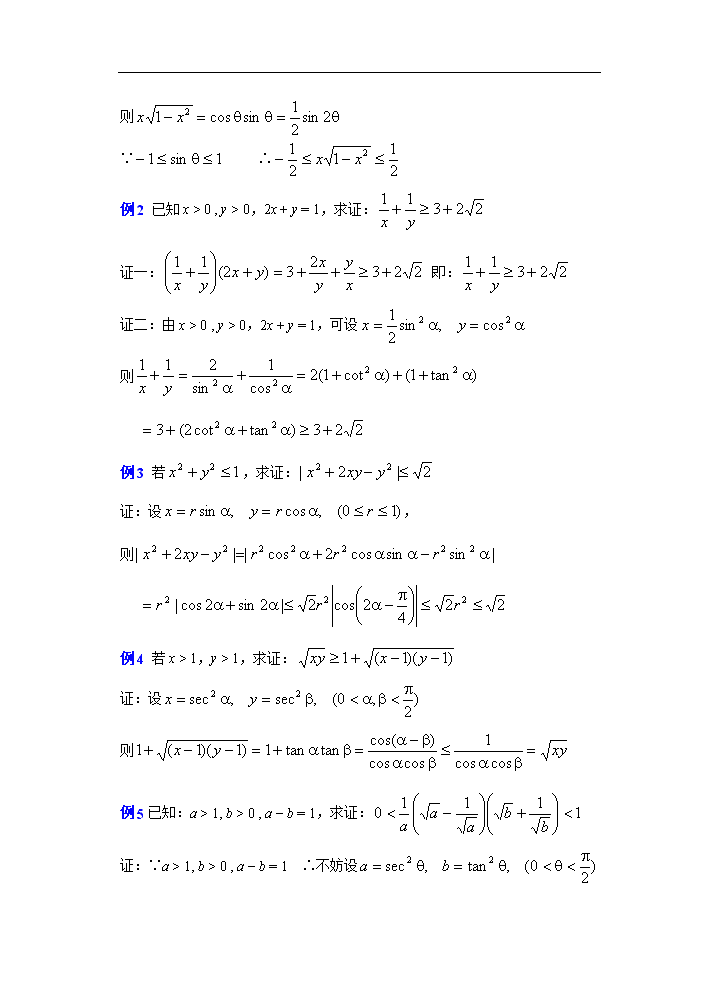高中数学第6章（第9课时）不等式的证明（4） 4页

课 题：不等式的证明（4）‎ 教学目的：‎ ‎ 1． 掌握换元法法证明不等式；‎ ‎2．理解换元法实质；‎ ‎3．提高证明不等式证法灵活性 教学重点：三角换元和代数换元 ‎ 教学难点： 三角换元 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程：‎ 一、复习引入：‎ ‎ 1．重要不等式：‎ 如果 ‎2．定理：如果a,b是正数，那么 ‎3公式的等价变形：ab≤，ab≤（）2‎ ‎4． ≥2（ab＞0），当且仅当a＝b时取“＝”号；‎ ‎5．定理：如果，那么（当且仅当时取“=”）‎ ‎6．推论：如果，那么 （当且仅当时取“=”）‎ ‎7．比较法之一（作差法）步骤：作差——变形——判断与0的关系——结论 比较法之二（作商法）步骤：作商——变形——判断与1的关系——结论 ‎8．综合法：利用某些已经证明过的不等式（例如算术平均数与几何平均数定理）和不等式的性质推导出所要证明的不等式成立，这种证明方法叫做综合法 用综合法证明不等式的逻辑关系是：‎ 综合法的思维特点是：由因导果，即由已知条件出发，利用已知的数学定理、性质和公式，推出结论的一种证明方法 ‎9分析法：‎ 证明不等式时，有时可以从求证的不等式出发，分析使这个不等式成立的条件，把证明不等式转化为判定这些条件是否具备的问题，如果能够肯定这些条件都已具备，那么就可以断定原不等式成立，这种方法叫做分析法 用分析法证明不等式的逻辑关系是：‎ 分析法的思维特点是：执果索因 分析法的书写格式：‎ ‎ 要证明命题B为真，‎ ‎ 只需要证明命题为真，从而有……‎ ‎ 这只需要证明命题为真，从而又有……‎ ‎ ……‎ 这只需要证明命题A为真 而已知A为真，故命题B必为真 二、讲解新课：‎ ‎1三角换元：‎ 若0≤x≤1，则可令x = sinq ()或x = sin2q ()‎ 若，则可令x = cosq , y = sinq ()‎ 若，则可令x = secq, y = tanq ()‎ 若x≥1，则可令x = secq ()‎ 若xÎR，则可令x = tanq ()‎ ‎2代数换元：‎ ‎“整体换元”,“均值换元”,“设差换元”的方法 三、讲解范例：‎ 例1 求证：‎ 证一：（综合法）‎ ‎∵‎ 即 ∴‎ 证二：（换元法） ∵ ∴令 x = cosq , qÎ[0, p]‎ 则 ‎∵ ∴‎ 例2 已知x > 0 , y > 0，2x + y = 1，求证：‎ 证一： 即：‎ 证二：由x > 0 , y > 0，2x + y = 1，可设 则 例3 若，求证：‎ 证：设， ‎ 则 例4 若x > 1，y > 1，求证： ‎ 证：设 则 例5已知：a > 1, b > 0 , a - b = 1，求证：‎ 证：∵a > 1, b > 0 , a - b = 1 ∴不妨设 ‎ 则 ‎∵, ∴0 < sinq < 1 ∴‎ 例6证明：若a > 0，则 证：设 则 ‎ （ 当a = 1时取“=” ）‎ ‎∴‎ 即 ∴原式成立 四、课堂练习：‎ 五、小结 ：‎ 六、课后作业：‎  七、板书设计（略）‎ 八、课后记：‎ ‎ ‎