2014年天津市高考数学试卷（文科） 23页

‎2014年天津市高考数学试卷（文科）‎ ‎　‎ 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）i是虚数单位，复数=（　　）‎ A．1﹣i B．﹣1+i C．+i D．﹣+i ‎2．（5分）设变量x，y满足约束条件，则目标函数z=x+2y的最小值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎3．（5分）已知命题p：∀x＞0，总有（x+1）ex＞1，则￢p为（　　）‎ A．∃x0≤0，使得（x0+1）e≤1 B．∃x0＞0，使得（x0+1）e≤1‎ C．∀x＞0，总有（x+1）ex≤1 D．∀x≤0，总有（x+1）ex≤1‎ ‎4．（5分）设a=log2π，b=logπ，c=π﹣2，则（　　）‎ A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞b＞a ‎5．（5分）设{an}的首项为a1，公差为﹣1的等差数列，Sn为其前n项和，若S1，S2，S4成等比数列，则a1=（　　）‎ A．2 B．﹣2 C． D．﹣‎ ‎6．（5分）已知双曲线﹣=1（a＞0，b＞0）的一条渐近线平行于直线l：y=2x+10，双曲线的一个焦点在直线l上，则双曲线的方程为（　　）‎ A．﹣=1 B．﹣=1‎ C．﹣=1 D．﹣=1‎ ‎7．（5分）如图，△ABC是圆的内接三角形，∠‎ BAC的平分线交圆于点D，交BC于E，过点B的圆的切线与AD的延长线交于点F，在上述条件下，给出下列四个结论：‎ ‎①BD平分∠CBF；‎ ‎②FB2=FD•FA；‎ ‎③AE•CE=BE•DE；‎ ‎④AF•BD=AB•BF．‎ 所有正确结论的序号是（　　）‎ A．①② B．③④ C．①②③ D．①②④‎ ‎8．（5分）已知函数f（x）=sinωx+cosωx（ω＞0），x∈R，在曲线y=f（x）与直线y=1的交点中，若相邻交点距离的最小值为，则f（x）的最小正周期为（　　）‎ A． B． C．π D．2π ‎　‎ 二、填空题：本大题共6小题，每小题5分，共30分.‎ ‎9．（5分）某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方向，从该校四个年级的本科生中抽取一个容量为300的样本进行调查，已知该校一年级、二年级、三年级、四年级的本科生人数之比为4：5：5：6，则应从一年级本科生中抽取　　名学生．‎ ‎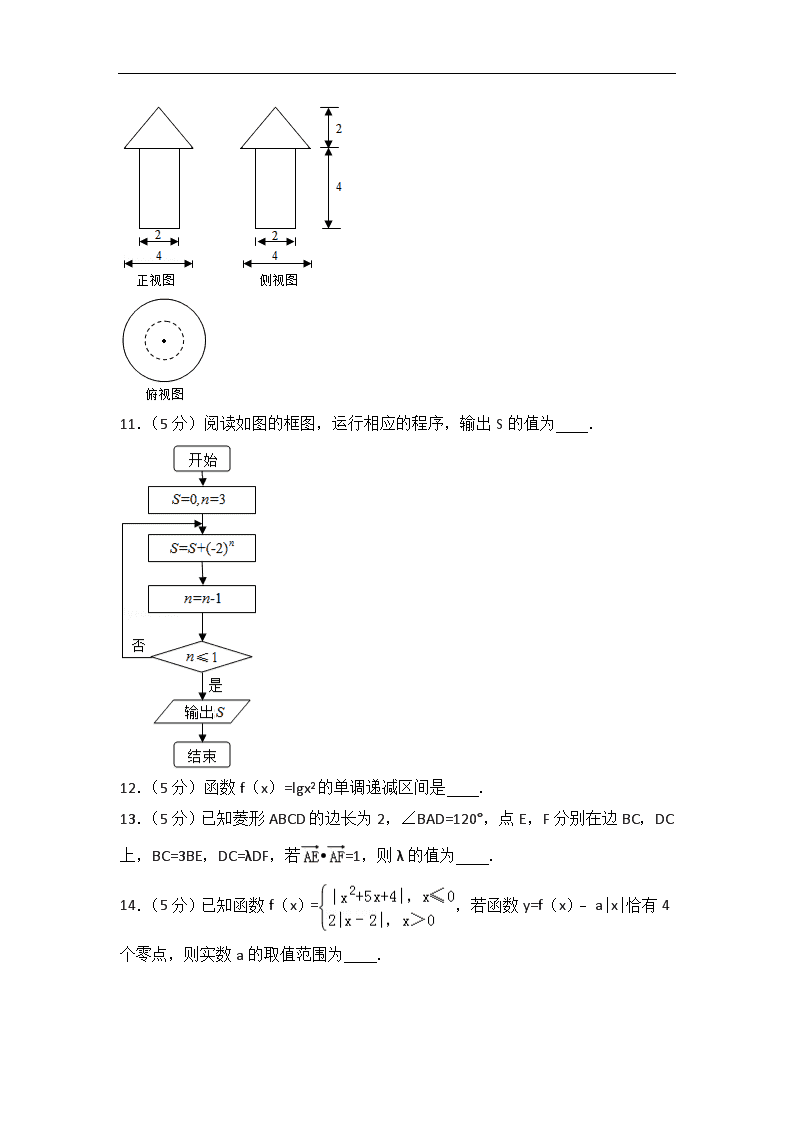10．（5分）一个几何体的三视图如图所示（单位：m），则该几何体的体积为　　m3．‎ ‎11．（5分）阅读如图的框图，运行相应的程序，输出S的值为　　．‎ ‎12．（5分）函数f（x）=lgx2的单调递减区间是　　．‎ ‎13．（5分）已知菱形ABCD的边长为2，∠BAD=120°，点E，F分别在边BC，DC上，BC=3BE，DC=λDF，若•=1，则λ的值为　　．‎ ‎14．（5分）已知函数f（x）=，若函数y=f（x）﹣a|x|恰有4个零点，则实数a的取值范围为　　．‎ ‎　‎ 三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.‎ ‎15．（13分）某校夏令营有3名男同学，A、B、C和3名女同学X，Y，Z，其年级情况如表：‎ 一年级 二年级 三年级 男同学 A B C 女同学 X Y Z 现从这6名同学中随机选出2人参加知识竞赛（每人被选到的可能性相同）‎ ‎（Ⅰ）用表中字母列举出所有可能的结果；‎ ‎（Ⅱ）设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件M发生的概率．‎ ‎16．（13分）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知a﹣c=b，sinB=sinC，‎ ‎（Ⅰ）求cosA的值；‎ ‎（Ⅱ）求cos（2A﹣）的值．‎ ‎17．（13分）如图，四棱锥P﹣ABCD的底面ABCD是平行四边形，BA=BD=，AD=2，PA=PD=，E，F分别是棱AD，PC的中点．‎ ‎（Ⅰ）证明EF∥平面PAB；‎ ‎（Ⅱ）若二面角P﹣AD﹣B为60°，‎ ‎（i）证明平面PBC⊥平面ABCD；‎ ‎（ii）求直线EF与平面PBC所成角的正弦值．‎ ‎18．（13分）设椭圆+=1（a＞b＞0）的左、右焦点分别为F1、F2，右顶点为A，上顶点为B，已知|AB|=|F1F2|．‎ ‎（Ⅰ）求椭圆的离心率；‎ ‎（Ⅱ）设P为椭圆上异于其顶点的一点，以线段PB为直径的圆经过点F1，经过点F2的直线l与该圆相切于点M，|MF2|=2，求椭圆的方程．‎ ‎19．（14分）已知函数f（x）=x2﹣ax3（a＞0），x∈R．‎ ‎（Ⅰ）求f（x）的单调区间和极值；‎ ‎（Ⅱ）若对于任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）•f（x2）=1，求a的取值范围．‎ ‎20．（14分）已知q和n均为给定的大于1的自然数，设集合M={0，1，2，…，q﹣1}，集合A={x|x=x1+x2q+…+xnqn﹣1，xi∈M，i=1，2，…n}．‎ ‎（Ⅰ）当q=2，n=3时，用列举法表示集合A；‎ ‎（Ⅱ）设s，t∈A，s=a1+a2q+…+anqn﹣1，t=b1+b2q+…+bnqn﹣1，其中ai，bi∈M，i=1，2，…，n．证明：若an＜bn，则s＜t．‎ ‎　‎ ‎2014年天津市高考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）（2014•天津）i是虚数单位，复数=（　　）‎ A．1﹣i B．﹣1+i C．+i D．﹣+i ‎【分析】将复数的分子与分母同时乘以分母的共轭复数3﹣4i，即求出值．‎ ‎【解答】解：复数==，‎ 故选A．‎ ‎　‎ ‎2．（5分）（2014•天津）设变量x，y满足约束条件，则目标函数z=x+2y的最小值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎【分析】作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．‎ ‎【解答】解：作出不等式对应的平面区域，‎ 由z=x+2y，得y=﹣，‎ 平移直线y=﹣，由图象可知当直线y=﹣经过点B（1，1）时，直线y=﹣的截距最小，此时z最小．‎ 此时z的最小值为z=1+2×1=3，‎ 故选：B．‎ ‎　‎ ‎3．（5分）（2014•天津）已知命题p：∀x＞0，总有（x+1）ex＞1，则￢p为（　　）‎ A．∃x0≤0，使得（x0+1）e≤1 B．∃x0＞0，使得（x0+1）e≤1‎ C．∀x＞0，总有（x+1）ex≤1 D．∀x≤0，总有（x+1）ex≤1‎ ‎【分析】据全称命题的否定为特称命题可写出命题p的否定．‎ ‎【解答】解：根据全称命题的否定为特称命题可知，￢p为∃x0＞0，使得（x0+1）e≤1，‎ 故选：B．‎ ‎　‎ ‎4．（5分）（2014•天津）设a=log2π，b=logπ，c=π﹣2，则（　　）‎ A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞b＞a ‎【分析】根据对数函数和幂函数的性质求出，a，b，c的取值范围，即可得到结论．‎ ‎【解答】解：log2π＞1，logπ＜0，0＜π﹣2＜1，‎ 即a＞1，b＜0，0＜c＜1，‎ ‎∴a＞c＞b，‎ 故选：C ‎　‎ ‎5．（5分）（2014•天津）设{an}的首项为a1，公差为﹣1的等差数列，Sn为其前n项和，若S1，S2，S4成等比数列，则a1=（　　）‎ A．2 B．﹣2 C． D．﹣‎ ‎【分析】由等差数列的前n项和求出S1，S2，S4，然后再由S1，S2，S4成等比数列列式求解a1．‎ ‎【解答】解：∵{an}是首项为a1，公差为﹣1的等差数列，Sn为其前n项和，‎ ‎∴S1=a1，S2=2a1﹣1，S4=4a1﹣6，‎ 由S1，S2，S4成等比数列，得：，‎ 即，解得：．‎ 故选：D．‎ ‎　‎ ‎6．（5分）（2014•天津）已知双曲线﹣=1（a＞0，b＞0）的一条渐近线平行于直线l：y=2x+10，双曲线的一个焦点在直线l上，则双曲线的方程为（　　）‎ A．﹣=1 B．﹣=1‎ C．﹣=1 D．﹣=1‎ ‎【分析】先求出焦点坐标，利用双曲线﹣=1（a＞0，b＞0）的一条渐近线平行于直线l：y=2x+10，可得=2，结合c2=a2+b2，求出a，b，即可求出双曲线的方程．‎ ‎【解答】解：∵双曲线的一个焦点在直线l上，‎ 令y=0，可得x=﹣5，即焦点坐标为（﹣5，0），∴c=5，‎ ‎∵双曲线﹣=1（a＞0，b＞0）的一条渐近线平行于直线l：y=2x+10，‎ ‎∴=2，‎ ‎∵c2=a2+b2，‎ ‎∴a2=5，b2=20，‎ ‎∴双曲线的方程为﹣=1．‎ 故选：A．‎ ‎　‎ ‎7．（5分）（2014•天津）如图，△ABC是圆的内接三角形，∠BAC的平分线交圆于点D，交BC于E，过点B的圆的切线与AD的延长线交于点F，在上述条件下，给出下列四个结论：‎ ‎①BD平分∠CBF；‎ ‎②FB2=FD•FA；‎ ‎③AE•CE=BE•DE；‎ ‎④AF•BD=AB•BF．‎ 所有正确结论的序号是（　　）‎ A．①② B．③④ C．①②③ D．①②④‎ ‎【分析】本题利用角与弧的关系，得到角相等，再利用角相等推导出三角形相似，得到边成比例，即可选出本题的选项．‎ ‎【解答】解：∵圆周角∠DBC对应劣弧CD，圆周角∠DAC对应劣弧CD，‎ ‎∴∠DBC=∠DAC．‎ ‎∵弦切角∠FBD对应劣弧BD，圆周角∠BAD对应劣弧BD，‎ ‎∴∠FBD=∠BAF．‎ ‎∵AD是∠BAC的平分线，‎ ‎∴∠BAF=∠DAC．‎ ‎∴∠DBC=∠FBD．即BD平分∠CBF．即结论①正确．‎ 又由∠FBD=∠FAB，∠BFD=∠AFB，得△FBD～△FAB．‎ 由，FB2=FD•FA．即结论②成立．‎ 由，得AF•BD=AB•BF．即结论④成立．‎ 正确结论有①②④．‎ 故答案为D ‎　‎ ‎8．（5分）（2014•天津）已知函数f（x）=sinωx+cosωx（ω＞0），x∈R，在曲线y=f（x）与直线y=1的交点中，若相邻交点距离的最小值为，则f（x）的最小正周期为（　　）‎ A． B． C．π D．2π ‎【分析】根据f（x）=2sin（ωx+），再根据曲线y=f（x）与直线y=1的交点中，相邻交点距离的最小值为，正好等于f（x）的周期的倍，求得函数f（x）的周期T的值．‎ ‎【解答】解：∵已知函数f（x）=sinωx+cosωx=2sin（ωx+）（ω＞0），x∈R，‎ 在曲线y=f（x）与直线y=1的交点中，若相邻交点距离的最小值为，正好等于f（x）的周期的倍，‎ 设函数f（x）的最小正周期为T，则=，∴T=π，‎ 故选：C．‎ ‎　‎ 二、填空题：本大题共6小题，每小题5分，共30分.‎ ‎9．（5分）（2014•天津）某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方向，从该校四个年级的本科生中抽取一个容量为300的样本进行调查，已知该校一年级、二年级、三年级、四年级的本科生人数之比为4：5：5：6，则应从一年级本科生中抽取　60　名学生．‎ ‎【分析】先求出一年级本科生人数所占总本科生人数的比例，再用样本容量乘以该比列，即为所求．‎ ‎【解答】解：根据分层抽样的定义和方法，一年级本科生人数所占的比例为 ‎=，‎ 故应从一年级本科生中抽取名学生数为300×=60，‎ 故答案为：60．‎ ‎　‎ ‎10．（5分）（2014•天津）一个几何体的三视图如图所示（单位：m），则该几何体的体积为　　m3．‎ ‎【分析】几何体是圆锥与圆柱的组合体，判断圆柱与圆锥的高及底面半径，代入圆锥与圆柱的体积公式计算．‎ ‎【解答】解：由三视图知：几何体是圆锥与圆柱的组合体，‎ 其中圆柱的高为4，底面直径为2，圆锥的高为2，底面直径为4，‎ ‎∴几何体的体积V=π×12×4+×π×22×2=4π+π=π．‎ 故答案为：．‎ ‎　‎ ‎11．（5分）（2014•天津）阅读如图的框图，运行相应的程序，输出S的值为　﹣4　．‎ ‎【分析】写出前二次循环，满足判断框条件，输出结果．‎ ‎【解答】解：由框图知，第一次循环得到：S=﹣8，n=2；‎ 第二次循环得到：S=﹣4，n=1；退出循环，输出﹣4．‎ 故答案为：﹣4．‎ ‎　‎ ‎12．（5分）（2014•天津）函数f（x）=lgx2的单调递减区间是　（﹣∞，0）　．‎ ‎【分析】先将f（x）化简，注意到x≠0，即f（x）=2lg|x|，再讨论其单调性，从而确定其减区间；也可以函数看成由复合而成，再分别讨论内层函数和外层函数的单调性，根据“同増异减”再来判断．‎ ‎【解答】解：方法一：y=lgx2=2lg|x|，‎ ‎∴当x＞0时，f（x）=2lgx在（0，+∞）上是增函数；‎ 当x＜0时，f（x）=2lg（﹣x）在（﹣∞，0）上是减函数．‎ ‎∴函数f（x）=lgx2的单调递减区间是（﹣∞，0）．‎ 故答案为：（﹣∞，0）．‎ 方法二：原函数是由复合而成，‎ ‎∵t=x2在（﹣∞，0）上是减函数，在（0，+∞）为增函数；‎ 又y=lgt在其定义域上为增函数，‎ ‎∴f（x）=lgx2在（﹣∞，0）上是减函数，在（0，+∞）为增函数，‎ ‎∴函数f（x）=lgx2的单调递减区间是（﹣∞，0）．‎ 故答案为：（﹣∞，0）．‎ ‎　‎ ‎13．（5分）（2014•天津）已知菱形ABCD的边长为2，∠BAD=120°，点E，F分别在边BC，DC上，BC=3BE，DC=λDF，若•=1，则λ的值为　2　．‎ ‎【分析】根据向量的基本定理，结合数量积的运算公式，建立方程即可得到结论．‎ ‎【解答】解：∵BC=3BE，DC=λDF，‎ ‎∴=，=，‎ ‎=+=+=+，=+=+=+，‎ ‎∵菱形ABCD的边长为2，∠BAD=120°，‎ ‎∴||=||=2，•=2×2×cos120°=﹣2，‎ ‎∵•=1，‎ ‎∴（+）•（+）=++（1+）•=1，‎ 即×4+×4﹣2（1+）=1，‎ 整理得，‎ 解得λ=2，‎ 故答案为：2．‎ ‎　‎ ‎14．（5分）（2014•天津）已知函数f（x）=‎ ‎，若函数y=f（x）﹣a|x|恰有4个零点，则实数a的取值范围为　（1，2）　．‎ ‎【分析】由y=f（x）﹣a|x|=0得f（x）=a|x|，利用数形结合即可得到结论．‎ ‎【解答】解：由y=f（x）﹣a|x|=0得f（x）=a|x|，‎ 作出函数y=f（x），y=a|x|的图象，‎ 当a≤0，不满足条件，‎ ‎∴a＞0，‎ 当a≥2时，此时y=a|x|与f（x）有三个 交点，‎ 当a=1时，‎ 当x＜0时，f（x）=﹣x2﹣5x﹣4，‎ 由f（x）=﹣x2﹣5x﹣4=﹣x 得x2+4x+4=0，‎ 则判别式△=16﹣4×4=0，‎ 即此时直线y=﹣x与f（x）相切，‎ 此时y=a|x|与f（x）有五个交点，‎ ‎∴要使函数y=f（x）﹣a|x|恰有4个零点，‎ 则1＜a＜2，‎ 故答案为：（1，2）‎ ‎　‎ 三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.‎ ‎15．（13分）（2014•天津）某校夏令营有3名男同学，A、B、C和3名女同学X，Y，Z，其年级情况如表：‎ 一年级 二年级 三年级 男同学 A B C 女同学 X Y Z 现从这6名同学中随机选出2人参加知识竞赛（每人被选到的可能性相同）‎ ‎（Ⅰ）用表中字母列举出所有可能的结果；‎ ‎（Ⅱ）设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件M发生的概率．‎ ‎【分析】（Ⅰ）用表中字母一一列举出所有可能的结果，共15个．‎ ‎（Ⅱ）用列举法求出事件M包含的结果有6个，而所有的结果共15个，由此求得事件M发生的概率．‎ ‎【解答】解：（Ⅰ）用表中字母列举出所有可能的结果有：（A，B）、（A，C）、（A，X）、（A，Y）、（A，Z）、‎ ‎（B，C）、（B，X）、（B，Y）、（B，Z）、（C，X）、（C，Y）、（C，Z）、（X，Y）、‎ ‎（X，Z ）、（Y，Z），共计15个结果．‎ ‎（Ⅱ）设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，‎ 则事件M包含的结果有：（A，Y）、（A，Z）、（B，X）、（B，Z）、（C，X）、（C，Y），共计6个结果，‎ 故事件M发生的概率为 =．‎ ‎　‎ ‎16．（13分）（2014•天津）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知a﹣c=b，sinB=sinC，‎ ‎（Ⅰ）求cosA的值；‎ ‎（Ⅱ）求cos（2A﹣）的值．‎ ‎【分析】‎ ‎（Ⅰ）已知第二个等式利用正弦定理化简，代入第一个等式表示出a，利用余弦定理表示出cosA，将表示出的a，b代入计算，即可求出cosA的值；‎ ‎（Ⅱ）由cosA的值，利用同角三角函数间的基本关系求出sinA的值，进而利用二倍角的正弦、余弦函数公式求出sin2A与cos2A的值，原式利用两角和与差的余弦函数公式及特殊角的三角函数值化简，将各自的值代入计算即可求出值．‎ ‎【解答】解：（Ⅰ）将sinB=sinC，利用正弦定理化简得：b=c，‎ 代入a﹣c=b，得：a﹣c=c，即a=2c，‎ ‎∴cosA===；‎ ‎（Ⅱ）∵cosA=，A为三角形内角，‎ ‎∴sinA==，‎ ‎∴cos2A=2cos2A﹣1=﹣，sin2A=2sinAcosA=，‎ 则cos（2A﹣）=cos2Acos+sin2Asin=﹣×+×=．‎ ‎　‎ ‎17．（13分）（2014•天津）如图，四棱锥P﹣ABCD的底面ABCD是平行四边形，BA=BD=，AD=2，PA=PD=，E，F分别是棱AD，PC的中点．‎ ‎（Ⅰ）证明EF∥平面PAB；‎ ‎（Ⅱ）若二面角P﹣AD﹣B为60°，‎ ‎（i）证明平面PBC⊥平面ABCD；‎ ‎（ii）求直线EF与平面PBC所成角的正弦值．‎ ‎【分析】（Ⅰ）要证明EF∥平面PAB，可以先证明平面EFH∥平面PAB，而要证明面面平行则可用面面平行的判定定理来证；‎ ‎（Ⅱ）（i）要证明平面PBC⊥平面ABCD，可用面面垂直的判定定理，即只需证PB⊥平面ABCD即可；‎ ‎（ii）由（i）知，BD，BA，BP两两垂直，建立空间直角坐标系B﹣DAP，得到直线EF的方向向量与平面PBC法向量，其夹角的余弦值的绝对值即为所成角的正弦值．‎ ‎【解答】解：（Ⅰ）证明：连结AC，AC∩BD=H，‎ ‎∵底面ABCD是平行四边形，∴H为BD中点，‎ ‎∵E是棱AD的中点．∴在△ABD中，EH∥AB，‎ 又∵AB⊂平面PAB，EH⊄平面PAD，∴EH∥平面PAB．‎ 同理可证，FH∥平面PAB．‎ 又∵EH∩FH=H，∴平面EFH∥平面PAB，‎ ‎∵EF⊂平面EFH，∴EF∥平面PAB；‎ ‎（Ⅱ）（i）如图，连结PE，BE．‎ ‎∵BA=BD=，AD=2，PA=PD=，∴BE=1，PE=2．‎ 又∵E为AD的中点，∴BE⊥AD，PE⊥AD，‎ ‎∴∠PEB即为二面角P﹣AD﹣B的平面角，即∠PEB=60°，∴PB=．‎ ‎∵△PBD中，BD2+PB2=PD2，∴PB⊥BD，同理PB⊥BA，‎ ‎∴PB⊥平面ABD，‎ ‎∵PB⊂平面PBC，∴平面PAB⊥平面ABCD；‎ ‎（ii）由（i）知，PB⊥BD，PB⊥BA，‎ ‎∵BA=BD=，AD=2，∴BD⊥BA，‎ ‎∴BD，BA，BP两两垂直，‎ 以B为坐标原点，分别以BD，BA，BP为X，Y，Z轴，建立如图所示的空间直角坐标系B﹣DAP，‎ 则有A（0，，0），B（0，0，0），C（，﹣，0），D（，0，0），P（0，0，），‎ ‎∴=（，﹣，0），=（0，0，），‎ 设平面PBC的法向量为，‎ ‎∵，∴，令x=1，则y=1，z=0，‎ 故=（1，1，0），‎ ‎∵E，F分别是棱AD，PC的中点，‎ ‎∴E（，，0），F（，﹣，），‎ ‎∴=（0，，），‎ ‎∴sinθ====﹣，‎ 即直线EF与平面PBC所成角的正弦值为．‎ ‎　‎ ‎18．（13分）（2014•天津）设椭圆+=1（a＞b＞0）的左、右焦点分别为F1、F2，右顶点为A，上顶点为B，已知|AB|=|F1F2|．‎ ‎（Ⅰ）求椭圆的离心率；‎ ‎（Ⅱ）设P为椭圆上异于其顶点的一点，以线段PB为直径的圆经过点F1，经过点F2的直线l与该圆相切于点M，|MF2|=2，求椭圆的方程．‎ ‎【分析】（Ⅰ）分别用a，b，c表示出|AB|和|F1F2|，根据已知建立等式求得a和c的关系，进而求得离心率e．‎ ‎（Ⅱ）根据（1）中a和c的关系，用c表示出椭圆的方程，设出P点的坐标，根据PB为直径，推断出BF1⊥PF1，进而知两直线斜率相乘得﹣1，进而求得sinθ和cosθ，表示出P点坐标，利用P，B求得圆心坐标，则可利用两点间的距离公式分别表示出|OB|，|OF2|，利用勾股定理建立等式求得c，则椭圆的方程可得．‎ ‎【解答】解：（Ⅰ）依题意可知=•2c，‎ ‎∵b2=a2﹣c2，‎ ‎∴a2+b2=2a2﹣c2=3c2，‎ ‎∴a2=2c2，‎ ‎∴e==．‎ ‎（Ⅱ）由（Ⅰ）知a2=2c2，‎ ‎∴b2=a2﹣c2=c2，‎ ‎∴椭圆方程为+=1，B（0，c），F1（﹣c，0）‎ 设P点坐标（csinθ，ccosθ），以线段PB为直径的圆的圆心为O，‎ ‎∵PB为直径，‎ ‎∴BF1⊥PF1，‎ ‎∴kBF1•kPF1=•=﹣1，‎ 求得sinθ=﹣或0（舍去），‎ 由椭圆对称性可知，P在x轴下方和上方结果相同，只看在x轴上方时，‎ cosθ==，‎ ‎∴P坐标为（﹣c，c），‎ ‎∴圆心O的坐标为（﹣c，c），‎ ‎∴r=|OB|==c，|OF2|==c，‎ ‎∵r2+|MF2|2=|OF2|2，‎ ‎∴+8=c2，‎ ‎∴c2=3，‎ ‎∴a2=6，b2=3，‎ ‎∴椭圆的方程为+=1．‎ ‎　‎ ‎19．（14分）（2014•天津）已知函数f（x）=x2﹣ax3（a＞0），x∈R．‎ ‎（Ⅰ）求f（x）的单调区间和极值；‎ ‎（Ⅱ）若对于任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）•f（x2）=1，求a的取值范围．‎ ‎【分析】（Ⅰ）求导数，利用导数的正负，可得f（x）的单调区间，从而求出函数的极值；‎ ‎（Ⅱ）由f（0）=f（）=0及（Ⅰ）知，当x∈（0，）时，f（x）＞0；当x∈（，+∞）时，f（x）＜0．设集合A={f（x）|x∈（2，+∞）}，集合B={|x∈（1，+∞），f（x）≠0}，则对于任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）•f（x2）=1，等价于A⊆B，分类讨论，即可求a的取值范围．‎ ‎【解答】解：（Ⅰ）f′（x）=2x﹣2ax2=2x（1﹣ax），令f′（x）=0，解得x=0或x=．‎ 当x变化时，f′（x），f（x）的变化情况如下表：‎ x ‎（﹣∞，0）‎ ‎0‎ ‎（0，）‎ ‎（，+∞）‎ f′（x）‎ ‎﹣‎ ‎0‎ ‎+‎ ‎0‎ ‎﹣‎ f（x）‎ 递减 ‎0‎ 递增 递减 所以，f（x）的单调递减区间为：（﹣∞，0）和，单调递增区间为，‎ 当x=0时，有极小值f（0）=0，当x=时，有极大值f（）=；‎ ‎（Ⅱ）由f（0）=f（）=0及（Ⅰ）知，当x∈（0，）时，f（x）＞0；当x∈（，+∞）时，f（x）＜0．‎ 设集合A={f（x）|x∈（2，+∞）}，集合B={|x∈（1，+∞），f（x）≠0}，则对于任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）•f（x2）=1，等价于A⊆B，显然A≠∅‎ 下面分三种情况讨论：‎ ‎①当＞2，即0＜a＜时，由f（）=0可知，0∈A，而0∉B，∴A不是B的子集；‎ ‎②当1≤≤2，即时，f（2）≤0，且f（x）在（2，+∞）上单调递减，故A=（﹣∞，f（2）），∴A⊆（﹣∞，0）；由f（1）≥0，有f（x）在（1，+∞）上的取值范围包含（﹣∞，0），即（﹣∞，0）⊆B，∴A⊆B；‎ ‎③当＜1，即a＞时，有f（1）＜0，且f（x）在（1，+∞）上单调递减，故B=（，0），A=（﹣∞，f（2）），∴A不是B的子集．‎ 综上，a的取值范围是[]．‎ ‎　‎ ‎20．（14分）（2014•天津）已知q和n均为给定的大于1的自然数，设集合M={0，1，2，…，q﹣1}，集合A={x|x=x1+x2q+…+xnqn﹣1，xi∈M，i=1，2，…n}．‎ ‎（Ⅰ）当q=2，n=3时，用列举法表示集合A；‎ ‎（Ⅱ）设s，t∈A，s=a1+a2q+…+anqn﹣1，t=b1+b2q+…+bnqn﹣1，其中ai，bi∈M，i=1，2，…，n．证明：若an＜bn，则s＜t．‎ ‎【分析】（Ⅰ）当q=2，n=3时，M={0，1}，A={x|，xi∈M，i=1，2，3}．即可得到集合A．‎ ‎（Ⅱ）由于ai，bi∈M，i=1，2，…，n．an＜bn，可得an﹣bn≤﹣1．‎ 由题意可得s﹣t=（a1﹣b1）+（a2﹣b2）q+…++≤﹣[1+q+…+qn﹣2+qn﹣1]，‎ 再利用等比数列的前n项和公式即可得出．‎ ‎【解答】（Ⅰ）解：当q=2，n=3时，‎ M={0，1}，A={x|，xi∈M，i=1，2，3}．‎ 可得A={0，1，2，3，4，5，6，7}．‎ ‎（Ⅱ）证明：由设s，t∈A，s=a1+a2q+…+anqn﹣1，t=b1+b2q+…+bnqn﹣1，其中ai，bi∈M，i=1，2，…，n．an＜bn，∴an﹣bn≤﹣1．‎ 可得s﹣t=（a1﹣b1）+（a2﹣b2）q+…++‎ ‎≤﹣[1+q+…+qn﹣2+qn﹣1]‎ ‎=＜0．‎ ‎∴s＜t．‎ ‎　‎ 参与本试卷答题和审题的老师有：wdnah；maths；sxs123；刘长柏；王老师；caoqz；清风慕竹；任老师；sllwyn；szjzl；wsj1012；沂蒙松（排名不分先后）‎ ‎2017年2月3日