2020高中数学集合间的基本关系 6页

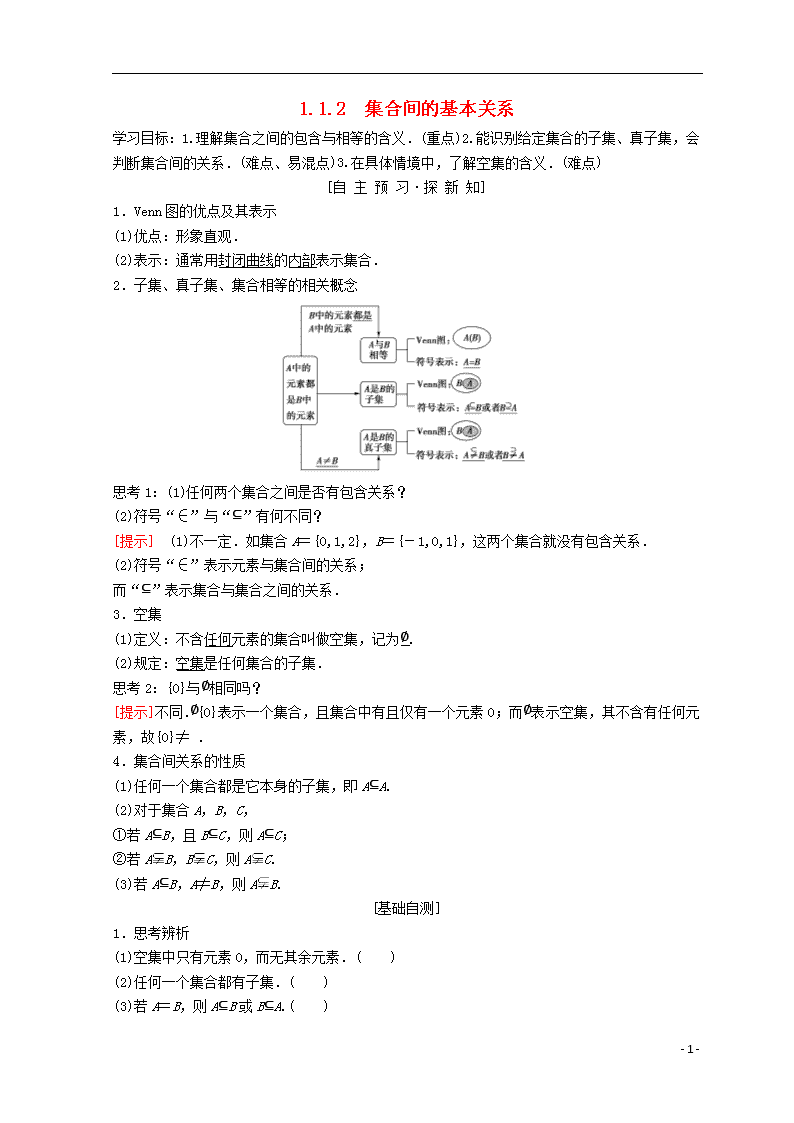
‎1.1.2　‎集合间的基本关系 学习目标：1.理解集合之间的包含与相等的含义．(重点)2.能识别给定集合的子集、真子集，会判断集合间的关系．(难点、易混点)3.在具体情境中，了解空集的含义．(难点)‎ ‎[自 主 预 习·探 新 知]‎ ‎1．Venn图的优点及其表示 ‎(1)优点：形象直观．‎ ‎(2)表示：通常用封闭曲线的内部表示集合．‎ ‎2．子集、真子集、集合相等的相关概念 思考1：(1)任何两个集合之间是否有包含关系？‎ ‎(2)符号“∈”与“⊆”有何不同？‎ ‎[提示]　(1)不一定．如集合A＝{0,1,2}，B＝{－1,0,1}，这两个集合就没有包含关系．‎ ‎(2)符号“∈”表示元素与集合间的关系；‎ 而“⊆”表示集合与集合之间的关系．‎ ‎3．空集 ‎(1)定义：不含任何元素的集合叫做空集，记为∅.‎ ‎(2)规定：空集是任何集合的子集．‎ 思考2：{0}与∅相同吗？‎ ‎[提示]不同．{0}表示一个集合，且集合中有且仅有一个元素0；而∅表示空集，其不含有任何元素，故{0}≠∅.‎ ‎4．集合间关系的性质 ‎(1)任何一个集合都是它本身的子集，即A⊆A.‎ ‎(2)对于集合A，B，C，‎ ‎①若A⊆B，且B⊆C，则A⊆C；‎ ‎②若AB，BC，则AC.‎ ‎(3)若A⊆B，A≠B，则AB.‎ ‎[基础自测]‎ ‎1．思考辨析 ‎(1)空集中只有元素0，而无其余元素．(　　)‎ ‎(2)任何一个集合都有子集．(　　)‎ ‎(3)若A＝B，则A⊆B或B⊆A.(　　)‎ - 6 -‎ ‎(4)空集是任何集合的真子集．(　　)‎ ‎[答案]　(1)×　(2)√　(3)√　(4)×‎ ‎2．下列四个集合中，是空集的为(　　)‎ A．{0}‎ B．{x|x>8，且x<5}‎ C．{x∈N|x2－1＝0}‎ D．{x|x>4}‎ B　[满足x>8且x<5的实数不存在，故{x|x>8，且x<5}＝∅.]‎ ‎3．已知集合M＝{菱形}，N＝{正方形}，则有(　　)‎ ‎【导学号：37102035】‎ A．M⊆N　　　　　　　　 B．M∈N C．N⊆M D．M＝N C　[正方形是特殊的菱形，故N⊆M.]‎ ‎4．集合{0,1}的子集有________个．‎ ‎4　[集合{0,1}的子集有∅，{0}，{1}，{0,1}，共4个．]‎ ‎[合 作 探 究·攻 重 难]‎ 集合间关系的判断 ‎　判断下列各组中集合之间的关系：‎ ‎(1)A＝{x|x是12的约数}，B＝{x|x是36的约数}．‎ ‎(2)A＝{x|x是平行四边形}，B＝{x|x是菱形}，C＝{x|x是四边形}，D＝{x|x是正方形}．‎ ‎(3)M＝，‎ N＝.‎ ‎[解]　(1)因为若x是12的约数，则必定是36的约数，反之不成立，所以.‎ ‎(2)由图形的特点可画出Venn图如图所示，从而.‎ ‎(3)对于集合M，其组成元素是，分子部分表示所有的整数；‎ 而对于集合N，其组成元素是＋n＝，分子部分表示所有的奇数．‎ 由真子集的概念知，.‎ ‎[规律方法]　判断集合关系的方法 (1)观察法：一一列举观察.‎ - 6 -‎ (2)元素特征法：首先确定集合的元素是什么，弄清集合元素的特征，再利用集合元素的特征判断关系.‎ (3)数形结合法：利用数轴或Venn图.‎ 提醒：若A⊆B和同时成立，则能准确表达集合A，B之间的关系.‎ ‎[跟踪训练]‎ ‎1．能正确表示集合M＝{x∈R|0≤x≤2}和集合N＝{x∈R|x2－x＝0}关系的Venn图是(　　) ‎ ‎【导学号：37102036】‎ B　[解x2－x＝0得x＝1或x＝0，故N＝{0,1}，易得NM，其对应的Venn图如选项B所示．]‎ ‎2．若集合A＝{x|－2＜x＜1}，B＝{x|x＜－1或x＞3}，则A∩B＝(　　)‎ A．{x|－2＜x＜－1}　　　　 B．{x|－2＜x＜3}‎ C．{x|－1＜x＜1} D．{x|1＜x＜3}‎ A　[∵A＝{x|－2＜x＜1}，B＝{x|x＜－1或x＞3}，‎ ‎∴A∩B＝{x|－2＜x＜－1}．故选A.]‎ 子集、真子集的个数问题 ‎　已知集合M满足{1,2}M⊆{1,2,3,4,5}，写出集合M所有的可能情况．‎ ‎[解]　由题意可以确定集合M必含有元素1,2，且至少含有元素3,4,5中的一个，因此依据集合M的元素个数分类如下：‎ 含有3个元素：{1,2,3}，{1,2,4}，{1,2,5}；‎ 含有4个元素：{1,2,3,4}，{1,2,3,5}，{1,2,4,5}；‎ 含有5个元素：{1,2,3,4,5}．‎ 故满足条件的集合M为{1,2,3}，{1,2,4}，{1,2,5}，{1,2,3,4}，{1,2,3,5}，{1,2,4,5}，{1,2,3,4,5}．‎ ‎[规律方法]　‎ 确定子集、真子集的三个关键点 有限集子集的确定问题，求解关键有三点：‎ (1)确定所求集合；‎ - 6 -‎ (2)合理分类，按照子集所含元素的个数依次写出，一般按元素从少到多的顺序逐个写出满足条件的集合；‎ (3)注意两个特殊的集合，即空集和集合本身.‎ ‎[跟踪训练]‎ ‎3．已知集合A＝{(x，y)|x＋y＝2，x，y∈N}，试写出A的所有子集及真子集. ‎ ‎【导学号：37102037】‎ ‎[解]　∵A＝{(x，y)|x＋y＝2，x，y∈N}，‎ ‎∴A＝{(0,2)，(1,1)，(2,0)}．‎ ‎∴A的子集有∅，{(0,2)}，{(1,1)}，{(2,0)}，{(0,2)，(1,1)}，{(0,2)，(2,0)}，{(1,1)，(2,0)}，{(0,2)，(1,1)，(2,0)}．‎ A的真子集有∅，{(0,2)}，{(1,1)}，{(2,0)}，{(0,2)，(1,1)}，{(0,2)，(2,0)}，{(1,1)，(2,0)}．‎ 由集合间的关系求参数 ‎[探究问题]‎ ‎1．若A＝{x|x>1}，B＝{x|x≥a}，若A⊆B，则实数a满足什么条件？若B⊆A呢？‎ 提示：如图(1)，若A⊆B，则a≤1；如图(2)，若B⊆A，则a>1.‎ ‎2．若集合A＝{x|11时，A中的元素是由满足不等式1‎2m－1，得m<2.‎ 综上可得，m的取值范围是m≤3.‎ 母题探究：1.若本例条件“A＝{x|－2≤x≤5}”改为“A＝{x|－2‎2m－1，得m<2.‎ ‎(2)当B≠∅时，如图所示 - 6 -‎ ‎∴解得即2≤m<3，‎ 综上可得，m的取值范围是m<3.‎ ‎2．若本例条件“BA”改为“A⊆B”，其他条件不变，求m的取值范围．‎ ‎[解]　当A⊆B时，如图所示，此时B≠∅.‎ ‎∴即∴m不存在．‎ 即不存在实数m使A⊆B.‎ ‎[规律方法]　‎ ‎1．利用集合的关系求参数问题 ‎(1)利用集合的关系求参数的范围问题，常涉及两个集合，其中一个为动集合(含参数)，另一个为静集合(具体的)，解答时常借助数轴来建立变量间的关系，需特别注意端点问题．‎ ‎(2)空集是任何集合的子集，因此在解A⊆B(B≠∅)的含参数的问题时，要注意讨论A＝∅和A≠∅两种情况，前者常被忽视，造成思考问题不全面．‎ ‎2．数学素养的建立 通过本例尝试建立数形结合的思想意识，以及在动态变化中学会用分类讨论的思想解决问题．‎ ‎[当 堂 达 标·固 双 基]‎ ‎1．已知集合A＝{x|－12.‎ ‎(2)若B⊆A，则集合B中的元素都在集合A中，则a≤2.‎ 因为a≥1，‎ 所以1≤a≤2.‎ - 6 -‎