- 145.00 KB
- 2021-06-23 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
等差数列的通项公式
(答题时间:40分钟)
*1. (扬州检测)在等差数列{an}中,已知a3=4,a5=-4,则a7=________。
*2. 已知点(1,1),(3,7)是等差数列{an}图象上的两点,则a5=________。
**3. 已知数列{an}满足:=+4,且a1=1,若an>0,则an=________。
*4. 已知等差数列{an}中,a3和a15是方程x2-6x-1=0的两个根,则a7+a8+a9+a10+a11=________。
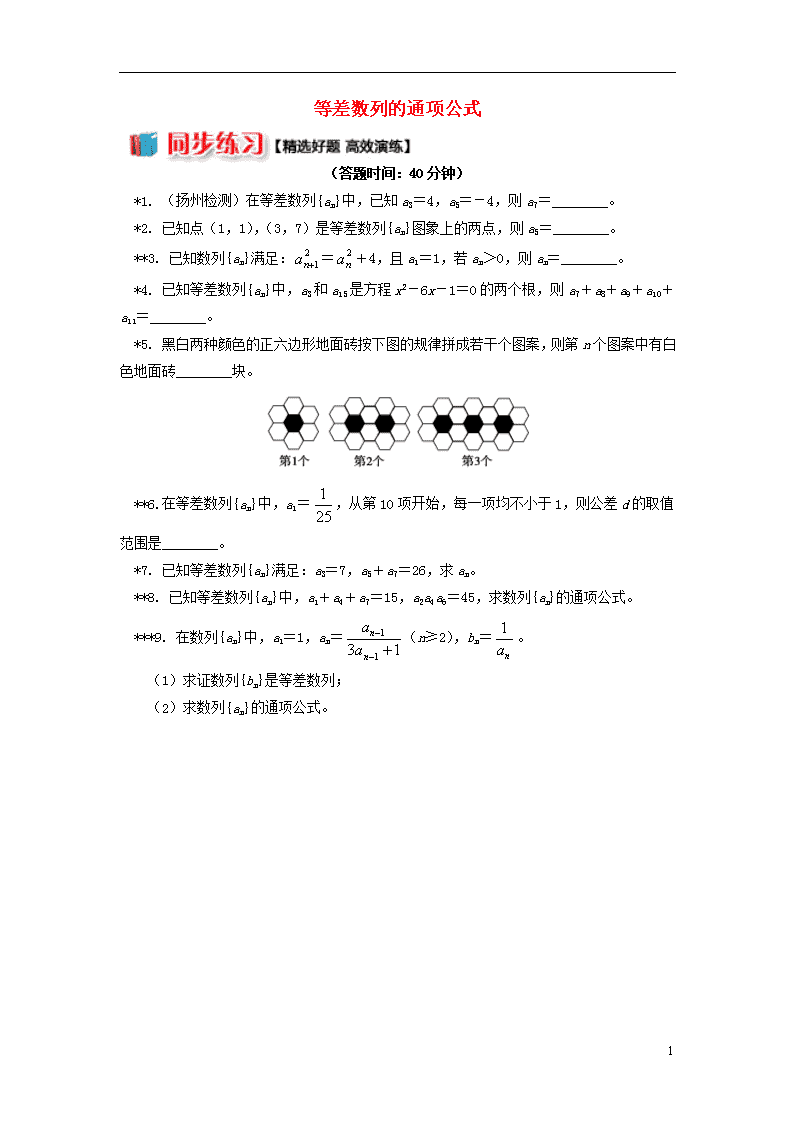
*5. 黑白两种颜色的正六边形地面砖按下图的规律拼成若干个图案,则第n个图案中有白色地面砖________块。
**6. 在等差数列{an}中,a1=,从第10项开始,每一项均不小于1,则公差d的取值范围是________。
*7. 已知等差数列{an}满足:a3=7,a5+a7=26,求an。
**8. 已知等差数列{an}中,a1+a4+a7=15,a2a4a6=45,求数列{an}的通项公式。
***9. 在数列{an}中,a1=1,an=(n≥2),bn=。
(1)求证数列{bn}是等差数列;
(2)求数列{an}的通项公式。
2
1. -12 解析:∵数列{an}是等差数列,∴a3+a7=2a5,
又∵a3=4,a5=-4,∴a7=2a5-a3=-12。
2. 13 解析:a1=1,2d=7-1,∴d=3,∴a5=a1+4d=1+4×3=13。
3. 解析:设=bn,则{bn}为等差数列,∵bn+1=bn+4且b1=1,∴bn=1+4(n-1)=4n-3,∴an==。
4. 15 解析:∵a3和a15是方程x2-6x-1=0的两根,
∴a3+a15=2a9=6,a9=3,
∴a7+a8+a9+a10+a11=(a7+a11)+(a8+a10)+a9=5a9=15。
5. 4n+2 解析:显然构成一个等差数列,且首项a1=6,公差d=4,∴第n个图案中有an=6+4(n-1)=4n+2块白色地面砖。
6. 解析:an=a1+(n-1)d=+(n-1)d,由题意知d>0,a10≥1且a9<1,即a10=+9d≥1且a9=+8d<1,解得。
7. 解:设等差数列{an}的公差为d,
∵a3=7,a5+a7=26,
∴解得
∴an=3+2(n-1)=2n+1。
8. 解:∵a1+a7=2a4,a1+a4+a7=3a4=15,
∴a4=5,
又∵a2a4a6=45,∴a2a6=9,
即(a4-2d)(a4+2d)=9,即(5-2d)(5+2d)=9,
解得d=±2。
若d=2,则an=a4+(n-4)·2=2n-3;
若d=-2,则an=a4+(n-4)·(-2)=13-2n。
9. (1)证明:由题意知bn-bn-1=-=3(n≥2,n∈N*),∴{bn}是公差为3的等差数列;
(2)解:∵a1=1,∴b1==1,∴bn=b1+(n-1)×3=3n-2=,∴an=(n∈N*)。
2
相关文档
- 专题37 两直线位置关系-备战2018高2021-06-2318页
- 高中数学选修第3章3_1_2同步练习2021-06-234页
- 绍兴市2019学年第一学期高中期末调2021-06-235页
- 高中数学:必修五 第三章 不等式习题2021-06-237页
- 湖北省黄冈中学高中数学竞赛(预赛)训2021-06-234页
- 高中数学(人教A版)必修3能力强化提升2021-06-235页
- 2020版高中数学 第2章 数列 第1课2021-06-237页
- 2020高中数学 课时分层作业9 复数2021-06-235页
- 高中数学必修2教案:3_1_2两条直线平2021-06-235页
- 高中数学必修5试题含答案2021-06-2313页