高中数学必修4：2_3_1平面向量基本定理(教、学案) 6页

‎2. 3.1‎‎ 平面向量基本定理 教学目标：‎ ‎（1）了解平面向量基本定理；‎ ‎（2）理解平面里的任何一个向量都可以用两个不共线的向量来表示，初步掌握应用向量 解决实际问题的重要思想方法；‎ ‎（3）能够在具体问题中适当地选取基底，使其他向量都能够用基底来表达. ‎ 教学重点：平面向量基本定理.‎ 教学难点：平面向量基本定理的理解与应用.‎ 教学过程：‎ 一、 复习引入：‎ ‎1．实数与向量的积：实数λ与向量的积是一个向量，记作：λ ‎（1）|λ|=|λ|||；（2）λ>0时λ与方向相同；λ<0时λ与方向相反；λ=0时λ=‎ ‎2．运算定律 结合律：λ(μ)=(λμ) ；分配律：(λ+μ)=λ+μ， λ(+)=λ+λ ‎ ‎3. 向量共线定理 向量与非零向量共线的充要条件是：有且只有一个非零实数λ，使=λ.‎ 二、讲解新课：‎ 平面向量基本定理：如果，是同一平面内的两个不共线向量，那么对于这一平面内的任一向量，有且只有一对实数λ1，λ2使=λ1+λ2.‎ 探究：‎ ‎(1) 我们把不共线向量ｅ１、ｅ２叫做表示这一平面内所有向量的一组基底；‎ ‎(2) 基底不惟一，关键是不共线；‎ ‎(3) 由定理可将任一向量a在给出基底ｅ１、ｅ２的条件下进行分解；‎ ‎(4) 基底给定时，分解形式惟一. 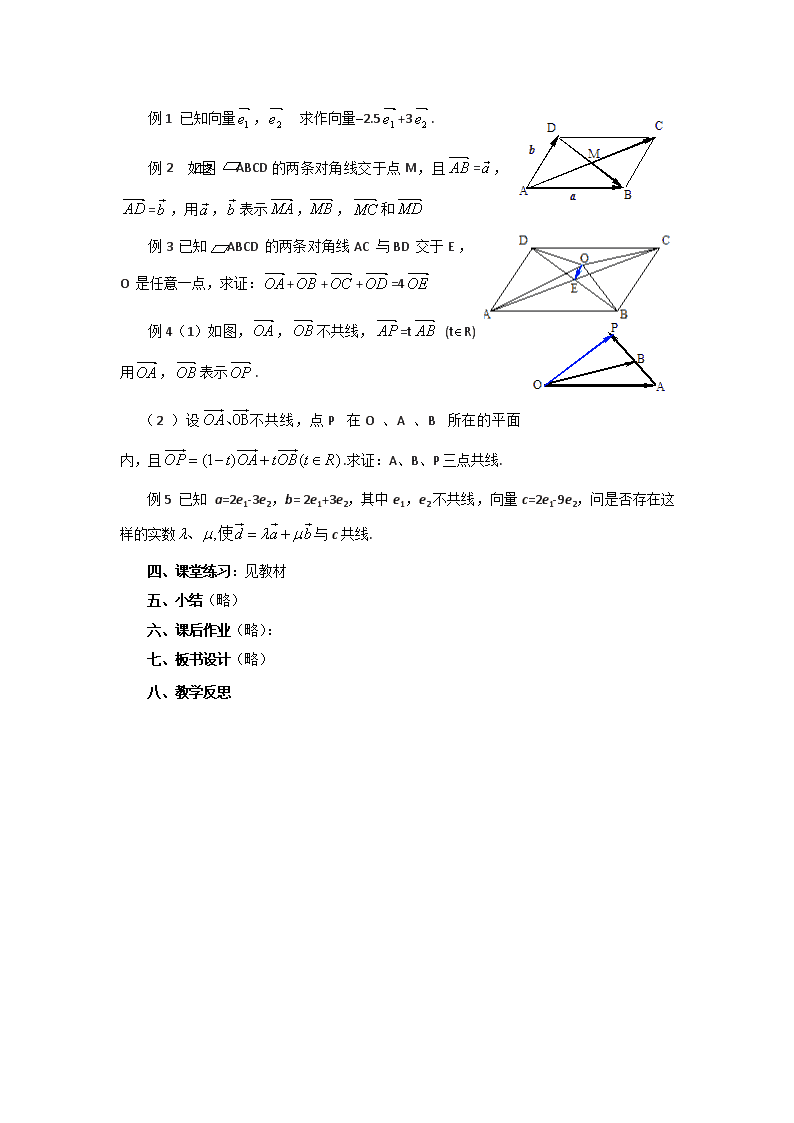λ1，λ2是被，，唯一确定的数量 三、讲解范例：‎ 例1 已知向量， 求作向量-2.5+3.‎ 例2 如图 ABCD的两条对角线交于点M，且=，=，用，表示，，和 ‎ 例3已知 ABCD的两条对角线AC与BD交于E，O是任意一点，求证：+++=4‎ 例4（1）如图，，不共线，=t (tÎR)用，表示.‎ ‎ （2）设不共线，点P在O、A、B所在的平面内，且.求证：A、B、P三点共线. ‎ 例5 已知 a=2e1-3e2，b= 2e1+3e2，其中e1，e2不共线，向量c=2e1-9e2，问是否存在这样的实数与c共线.‎ 四、课堂练习：见教材 五、小结（略） ‎ 六、课后作业（略）：‎ 七、板书设计（略）‎ 八、教学反思 ‎ ‎ ‎2.3.1‎平面向量的基本定理 课前预习学案 一、预习目标:通过回顾复习向量的线性运算,提出新的疑惑.为新授内容做好铺垫.‎ 二、预习内容 ‎ ‎（一）复习回顾 ‎1．实数与向量的积：实数λ与向量的积是一个向量，记作：λ ‎（1）|λ|= ；（2）λ>0时λ与方向 ；λ<0时λ与方向 ；λ=0时λ= ‎ ‎2．运算定律 结合律：λ(μ)= ；分配律：(λ+μ)= ， λ(+)= . ‎ ‎3. 向量共线定理 向量与非零向量共线的充要条件是：有且只有一个非零实数λ，使 .‎ ‎(二)阅读教材,提出疑惑:‎ 如何通过向量的线性运算来表示出平面内的任意向量?‎ 课内探究学案 一、学习目标 1、知道平面向量基本定理；‎ ‎ 2、理解平面里的任何一个向量都可以用两个不共线的向量来表示，初步应用向量解决实际问题；‎ ‎ 3、能够在具体问题中适当地选取基底，使其他向量都能够用基底来表示.‎ 学习重难点：‎ ‎1. 教学重点：平面向量基本定理 ‎ ‎2. 教学难点：平面向量基本定理的理解与应用 二、学习过程 ‎（一）定理探究：‎ 平面向量基本定理： ‎ ‎ ‎ ‎ ‎ 探究：‎ ‎(1) 我们把不共线向量ｅ１、ｅ２叫做表示这一平面内所有向量的 ;‎ ‎(2) 基底不惟一，关键是 ；‎ ‎(3) 由定理可将任一向量a在给出基底ｅ１、ｅ２的条件下进行分解；‎ ‎(4) 基底给定时，分解形式 . 即λ1，λ2是被，，唯一确定的数量 ‎（二）例题讲解 例1 已知向量， 求作向量-2.5+3.‎ 例2、如图 ABCD的两条对角线交于点M，且=，=，用，表示，，和 ‎ ‎ ‎ 例3已知 ABCD的两条对角线AC与BD交于E，O是任意一点，求证：+++=4‎ 例4（1）如图，，不共线，=t (tÎR)用，表示.‎ ‎ （2）设不共线，点P在O、A、B所在的平面内，且.求证：A、B、P三点共线. ‎ 例5 已知 a=2e1-3e2，b= 2e1+3e2，其中e1，e2不共线，向量c=2e1-9e2，问是否存在这样的实数与c共线.‎ ‎（三）反思总结 课后练习与提高 ‎1.设e1、e2是同一平面内的两个向量，则有( )‎ A.e1、e2一定平行 ‎ B.e1、e2的模相等 C.同一平面内的任一向量a都有a =λe1+μe2(λ、μ∈R)‎ D.若e1、e2不共线，则同一平面内的任一向量a都有a =λe1+ue2(λ、u∈R)‎ ‎2.已知向量a = e1-2e2，b =2e1+e2，其中e1、e2不共线，则a+b与c =6e1-2e2的关系 A.不共线 B.共线 C.相等 D.无法确定 ‎3.已知向量e1、e2不共线，实数x、y满足(3x-4y)e1+(2x-3y)e2=6e1+3e2，则x-y的值等于( )‎ A.3 B.‎-3 C.0 D.2‎ ‎4.已知a、b不共线，且c =λ‎1a+λ2b(λ1，λ2∈R)，若c与b共线，则λ1= .‎ ‎5.已知λ1＞0，λ2＞0，e1、e2是一组基底，且a =λ1e1+λ2e2，则a与e1_____，a与e2_________(填共线或不共线).‎ ‎ ‎