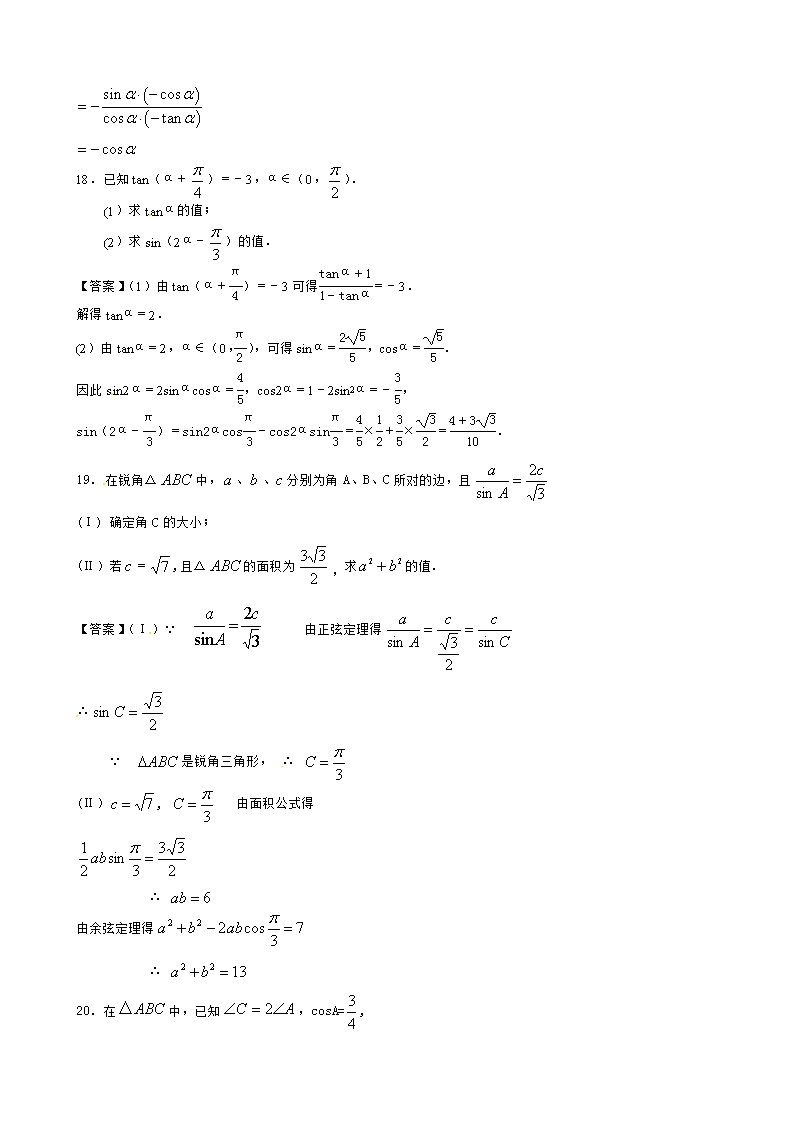2013版高考数学二轮复习专题训练：三角函数 4页

‎2013版高考数学二轮复习专题训练：三角函数 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．‎ 第Ⅰ卷(选择题　共60分)‎ 一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．已知扇形OAB的圆心角为，其面积是‎2cm2则该扇形的周长是( )cm。‎ A．8 B．‎6 ‎C．4 D．2‎ ‎【答案】B ‎2．函数 (x∈［-π,0］)的单调递增区间是( )‎ A． B． C． D．‎ ‎【答案】D ‎3．的值是( )‎ A． B． C． D． ‎ ‎【答案】D ‎4．已知D是由不等式组所确定的平面区域，则圆 在区域D内的弧长为( )‎ A ． B． C． D．‎ ‎【答案】B ‎5．下列命题正确的是( )‎ A．终边相同的角都相等 B．钝角比第三象限角小 C．第一象限角都是锐角 D．锐角都是第一象限角 ‎【答案】D ‎6．已知角的终边过点P(-4k,3k) (), 则的值是( )‎ A． B． ‎ C．或 D．随着k的取值不同其值不同 ‎【答案】B ‎7．sin585°的值为( )‎ A． B． C． D．‎ ‎【答案】A ‎8．若，则的值为( )‎ A．2 B．‎3 ‎C．4 D．6‎ ‎【答案】D ‎9．设锐角q使关于x的方程x2+4xcosq+cotq=0有重根，则q的弧度数为( )‎ A． B．或 C．或 D． ‎【答案】B ‎10．，则的值为( )‎ A． B． C． D． －‎ ‎【答案】A ‎11．°=( )‎ A． B． C． D． ‎ ‎【答案】C ‎12．若角的终边上有一点，且，则的值为( )‎ A． B． C．或 D． 或 ‎【答案】C 第Ⅱ卷(非选择题　共90分)‎ 二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)‎ ‎13．设,则的值为____________.‎ ‎【答案】‎ ‎14．在中，内角的对边分别是，若，，则 ．‎ ‎【答案】 30°‎ ‎15．已知扇形的周长为，圆心角为弧度，则该扇形的面积为____________‎ ‎【答案】9‎ ‎16．设扇形的周长为，面积为，则扇形的圆心角的弧度数是____________‎ ‎【答案】2‎ 三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17．化简 ‎【答案】‎ ‎ ‎ ‎ ‎ ‎18．已知tan（α＋）＝－3，α∈（0，）．‎ ‎ (1）求tanα的值；‎ ‎ (2）求sin（2α－）的值．‎ ‎【答案】（1）由tan（α＋）＝－3可得＝－3．‎ 解得tanα＝2．‎ ‎(2）由tanα＝2，α∈（0，），可得sinα＝，cosα＝．‎ 因此sin2α＝2sinαcosα＝，cos2α＝1－2sin2α＝－，‎ sin（2α－）＝sin2αcos－cos2αsin＝×＋×＝．‎ ‎19．在锐角△中，、、分别为角A、B、C所对的边，且 ‎ ‎(Ⅰ) 确定角C的大小；‎ ‎(Ⅱ）若＝,且△的面积为，求的值. ‎ ‎【答案】（Ⅰ）∵ 由正弦定理得 ‎∴ ‎ ‎ ∵ 是锐角三角形， ∴ ‎ ‎(Ⅱ）, 由面积公式得 ‎ ∴ ‎ 由余弦定理得 ‎ ∴ ‎ ‎20．在中，已知，cosA=, ‎ ‎(1）求的值； (2）求边的长。‎ ‎【答案】（1）∵ ，cosA=， 、、为的内角，‎ ‎ ∴ ，，‎ ‎∴ ，。‎ ‎(2）∵ ， ∴ ，。‎ 又由正弦定理，得，。‎ 由，，解得，。‎ ‎∴ ，，即边的长为5。‎ ‎21．已知.‎ ‎(1）求的值；（2）求的值.‎ ‎【答案】（1）‎ ‎(2）‎ ‎22．设f(x)＝，‎ ‎(1）求f(x)＋f(60°－x)（2）求f(1°)＋f(2°)＋…＋f(59°)的值 ‎【答案】（1）f(x)＋f(60°－x)＝＋＝ ‎＝＝，‎ ‎(2）f(x)＋f(60°－x)＝ ∴f(1°)＋f(2°)＋…＋f(59°)＝‎ ‎[f(1°)＋f(59°)]＋[f(2°)＋f(58°)]＋…＋[f(29°)＋f(31°)]＋f(30°)＝．‎