2020高中数学 第三章几类不同增长的函数模型 7页

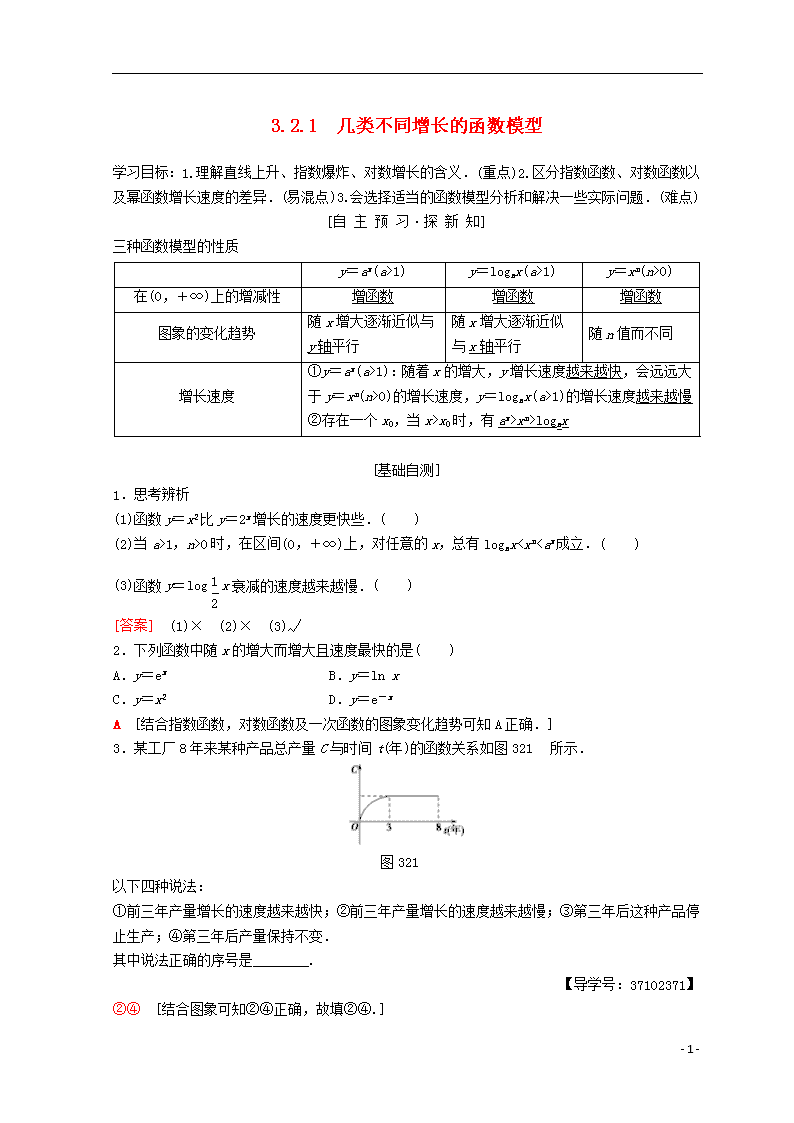
‎3.2.1　‎几类不同增长的函数模型 学习目标：1.理解直线上升、指数爆炸、对数增长的含义．(重点)2.区分指数函数、对数函数以及幂函数增长速度的差异．(易混点)3.会选择适当的函数模型分析和解决一些实际问题．(难点)‎ ‎[自 主 预 习·探 新 知]‎ 三种函数模型的性质 y＝ax(a>1)‎ y＝logax(a>1)‎ y＝xn(n>0)‎ 在(0，＋∞)上的增减性 增函数 增函数 增函数 图象的变化趋势 随x增大逐渐近似与y轴平行 随x增大逐渐近似与x轴平行 随n值而不同 增长速度 ‎①y＝ax(a>1)：随着x的增大，y增长速度越来越快，会远远大于y＝xn(n>0)的增长速度，y＝logax(a>1)的增长速度越来越慢 ‎②存在一个x0，当x>x0时，有ax>xn>logax ‎[基础自测]‎ ‎1．思考辨析 ‎(1)函数y＝x2比y＝2x增长的速度更快些．(　　)‎ ‎(2)当a>1，n>0时，在区间(0，＋∞)上，对任意的x，总有logax1时呈爆炸式增长，并且随a值的增大，增长速度越快，应选A.‎ ‎(2)观察函数f(x)＝logx，g(x)＝x与h(x)＝x在区间(0，＋∞)上的图象(如图)可知：‎ 函数f(x)的图象在区间(0,1)上递减较快，但递减速度逐渐变慢；在区间(1，＋∞)上，递减较慢，且越来越慢，同样，函数g(x)的图象在区间(0，＋∞)上，递减较慢，且递减速度越来越慢；函数h(x)的图象在区间(0,1)上递减较快，但递减速度逐渐变慢；在区间(1，＋∞)上，递减较慢，且越来越慢．]‎ ‎[规律方法]　常见的函数模型及增长特点 (1)线性函数模型 线性函数模型y＝kx＋b(k>0)的增长特点是直线上升，其增长速度不变. (2)指数函数模型 指数函数模型y＝ax(a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越快，即增长速度急剧，形象地称为“指数爆炸”. (3)对数函数模型 对数函数模型y＝logax(a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越慢，即增长速度平缓. (4)幂函数模型 - 7 -‎ 幂函数y＝xn(n>0)的增长速度介于指数增长和对数增长之间. ‎[跟踪训练]‎ ‎1．四个变量y1，y2，y3，y4随变量x变化的数据如表：‎ x ‎1‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ ‎30‎ y1‎ ‎2‎ ‎26‎ ‎101‎ ‎226‎ ‎401‎ ‎626‎ ‎901‎ y2‎ ‎2‎ ‎32‎ ‎1 024‎ ‎37 768‎ ‎1.05×106‎ ‎3.36×107‎ ‎1.07×109‎ y3‎ ‎2‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ y4‎ ‎2‎ ‎4.322‎ ‎5.322‎ ‎5.907‎ ‎6.322‎ ‎6.644‎ ‎6.907‎ 关于x呈指数函数变化的变量是________. 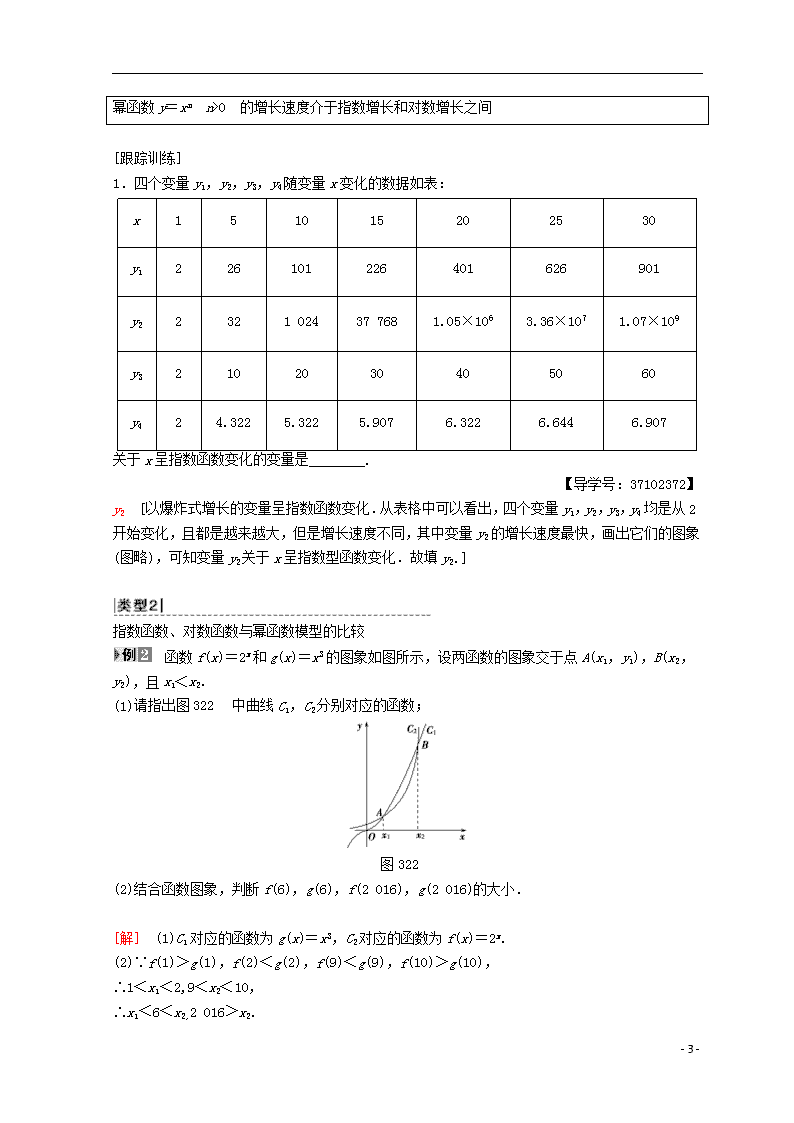‎ ‎【导学号：37102372】‎ y2　[以爆炸式增长的变量呈指数函数变化．从表格中可以看出，四个变量y1，y2，y3，y4均是从2开始变化，且都是越来越大，但是增长速度不同，其中变量y2的增长速度最快，画出它们的图象(图略)，可知变量y2关于x呈指数型函数变化．故填y2.]‎ 指数函数、对数函数与幂函数模型的比较 ‎　函数f(x)＝2x和g(x)＝x3的图象如图所示，设两函数的图象交于点A(x1，y1)，B(x2，y2)，且x1＜x2.‎ ‎(1)请指出图322中曲线C1，C2分别对应的函数；‎ 图322‎ ‎(2)结合函数图象，判断f(6)，g(6)，f(2 016)，g(2 016)的大小．‎ ‎[解]　(1)C1对应的函数为g(x)＝x3，C2对应的函数为f(x)＝2x.‎ ‎(2)∵f(1)＞g(1)，f(2)＜g(2)，f(9)＜g(9)，f(10)＞g(10)，‎ ‎∴1＜x1＜2,9＜x2＜10，‎ ‎∴x1＜6＜x2,2 016＞x2.‎ - 7 -‎ 从图象上可以看出，当x1＜x＜x2时，f(x)＜g(x)，‎ ‎∴f(6)＜g(6)；‎ 当x＞x2时，f(x)＞g(x)，‎ ‎∴f(2 016)＞g(2 016)．‎ 又g(2 016)＞g(6)，‎ ‎∴f(2 016)＞g(2 016)＞g(6)＞f(6)．‎ ‎[规律方法]　‎ 由图象判断指数函数、对数函数和幂函数的方法 根据图象判断增长型的指数函数、对数函数和幂函数时，通常是观察函数图象上升得快慢，即随着自变量的增大，图象最“陡”的函数是指数函数；图象趋于平缓的函数是对数函数．‎ ‎[跟踪训练]‎ ‎2．函数f(x)＝lg x，g(x)＝0.3x－1的图象如图323所示．‎ 图323‎ ‎(1)试根据函数的增长差异指出曲线C1，C2分别对应的函数；‎ ‎(2)比较两函数的增长差异(以两图象交点为分界点，对f(x)，g(x)的大小进行比较). ‎ ‎【导学号：37102373】‎ ‎[解]　(1)C1对应的函数为g(x)＝0.3x－1，C2对应的函数为f(x)＝lg x.‎ ‎(2)当xf(x)；当x1g(x)；当x>x2时，g(x)>f(x)；当x＝x1或x＝x2时，f(x)＝g(x)．‎ 需选择函数模型的实际问题 ‎[探究问题]‎ ‎1．一次函数模型、指数函数模型、对数函数模型的增长速度各有什么特点？‎ 提示：一次函数模型的增长速度不变，是均匀的；指数函数模型的增长速度最快，呈爆炸式；对数函数模型的增长速度先快后慢．‎ ‎2．在选择函数模型时，若随着自变量的变大、函数值增加得速度急剧变化，应选择哪个函数模型？若变化的速度很平缓，应选择哪个函数模型？‎ 提示：前者应选择指数函数模型，后者选择对数函数模型．‎ ‎　(1)某公司为了适应市场需求对产品结构做了重大调整，调整后初期利润增长迅速，后来增长越来越慢，若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系，可选用(　　)‎ A．一次函数 B．二次函数 C．指数型函数 D．对数型函数 - 7 -‎ ‎(2)某皮鞋厂今年1月份开始投产，并且前4个月的产量分别为1万双，1.2万双，1.3万双，1.37万双．由于产品质量好、款式新颖，前几个月的销售情况良好．为了推销员在推销产品时，接受订单不至于过多或过少，需要估计以后几个月的产量．厂里分析，产量的增加是由于工人生产熟练和理顺了生产流程．厂里也暂时不准备增加设备和工人．假如你是厂长，就月份为x，产量为y给出三种函数模型：y＝ax＋b，y＝ax2＋bx＋c，y＝abx＋c，你将利用哪一种模型去估算以后几个月的产量？‎ 思路探究：结合函数模型的增长速度选择合适的模型求解．‎ ‎(1)D　[结合“直线上升，对数增长，指数爆炸”可知，对数型函数符合题设条件，故选D.]‎ ‎(2)由题意知，将产量随时间变化的离散量分别抽象为A(1,1)，B(2,1.2)，C(3,1.3)，D(4,1.37)这4个数据．‎ ‎①设模拟函数为y＝ax＋b时，‎ 将B，C两点的坐标代入函数式，‎ 得解得 所以有关系式y＝0.1x＋1.‎ 由此可得结论为：在不增加工人和设备的条件下，产量会每月上升1 000双，这是不太可能的．‎ ‎②设模拟函数为y＝ax2＋bx＋c时，将A，B，C三点的坐标代入函数式，得 解得 所以有关系式y＝－0.05x2＋0.35x＋0.7.‎ 结论为：由此法计算4月份的产量为1.3万双，比实际产量少700双，而且由二次函数性质可知，产量自4月份开始将每月下降(图象开口向下，对称轴为x＝3.5)，不合实际．‎ ‎③设模拟函数为y＝abx＋c时，‎ 将A，B，C三点的坐标代入函数式，‎ 得 由1)，得ab＝1－c，代入2)3)，‎ 得 则解得则a＝＝－0.8.‎ 所以有关系式y＝－0.8×0.5x＋1.4.‎ 结论为：当把x＝4代入得y＝－0.8×0.54＋1.4＝1.35.‎ 比较上述三个模拟函数的优劣，既要考虑到误差最小，又要考虑生产的实际，如：增产的趋势和可能性．经过筛选，以指数函数模拟为最佳，一是误差小，二是由于厂房新建，随着工人技术和管理效益逐渐提高，一段时间内产量会明显上升，但经过一段时间之后，如果不更新设备，产量必然趋于稳定，而指数型函数模型恰好反映了这种趋势．‎ 因此选用指数型函数y＝－0.8×0.5x＋1.4，模拟比较接近客观实际．‎ ‎[规律方法]　(1)此类问题求解的关键是首先利用待定系数法求出相关函数模型，也就是借助数据信息，得到相关方程，进而求出待定参数. - 7 -‎ (2)函数模型的选择与数据的拟合是数学建模中最核心的内容，解题的关键在于通过对已知数据的分析，得出重要信息，根据解题积累的经验，从已有的各类型函数中选择模拟，进行数据的拟合. ‎[跟踪训练]‎ ‎3．某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5～8千美元的地区销售该公司A饮料的情况调查时发现：该饮料在人均GDP处于中等的地区销售量最多，然后向两边递减．‎ ‎(1)下列几个模拟函数中：①y＝ax2＋bx；②y＝kx＋b；③y＝logax＋b；④y＝ax＋b(x表示人均GDP，单位：千美元，y表示年人均A饮料的销售量，单位：L)．用哪个模拟函数来描述人均A饮料销售量与地区的人均GDP关系更合适？说明理由；‎ ‎(2)若人均GDP为1千美元时，年人均A饮料的销售量为‎2 L，人均GDP为4千美元时，年人均A饮料的销售量为‎5 L，把(1)中你所选的模拟函数求出来，并求出各个地区中，年人均A饮料的销售量最多是多少？ ‎ ‎【导学号：37102374】‎ ‎[解]　(1)用①来模拟比较合适．因为该饮料在人均GDP处于中等的地区销售量最多，然后向两边递减．而②，③，④表示的函数在区间上是单调函数，所以②，③，④都不合适，故用①来模拟比较合适．‎ ‎(2)因为人均GDP为1千美元时，年人均A饮料的销量为‎2升；人均GDP为4千美元时，年人均A饮料的销量为‎5升，把x＝1，y＝2；x＝4，y＝5代入到y＝ax2＋bx，得解得a＝－，b＝，所以函数解析式为y＝－x2＋x.(x∈[0.5,8])‎ ‎∵y＝－x2＋x＝－2＋，∴当x＝时，年人均A饮料的销售量最多是 L.‎ ‎[当 堂 达 标·固 双 基]‎ ‎1．如表是函数值y随自变量x变化的一组数据，由此判断它最可能的函数模型(　　)‎ x ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ y ‎15‎ ‎17‎ ‎19‎ ‎21‎ ‎23‎ ‎25‎ ‎27‎ A.一次函数模型　　　　 B．二次函数模型 C．指数函数模型 D．对数函数模型 A　[自变量每增加1函数值增加2，函数值的增量是均匀的，故为一次函数模型．故选A.]‎ ‎2．下列函数中，随x的增大，增长速度最快的是(　　) ‎ ‎【导学号：37102375】‎ A．y＝1 B．y＝x C．y＝3x D．y＝log3x C　[结合函数y＝1，y＝x，y＝3x及y＝log3x的图象可知(图略)，随着x的增大，增长速度最快的是y＝3x.]‎ ‎3．能使不等式log2x4时，log2xg(x)；‎ 当x＝4时，f(x)＝g(x)；‎ 当x>4时，f(x)