2020高中数学 课时分层作业17 空间向量运算的坐标表示 新人教A版选修2-1 6页

课时分层作业(十七) 空间向量运算的坐标表示 ‎(建议用时：40分钟)‎ ‎[基础达标练]‎ 一、选择题 ‎1．已知a＝(1，－2,1)，a－b＝(－1,2，－1)，则b＝(　　)‎ A．(2，－4,2)　　　　 B．(－2,4，－2)‎ C．(－2,0，－2) D．(2,1，－3)‎ A　[b＝a－(a－b)＝(1，－2,1)－(－1,2，－1)＝(2，－4,2)．]‎ ‎2．设A(3,3,1)，B(1,0,5)，C(0,1,0)，则AB的中点M到点C的距离|CM|的值为(　　)‎ A． B． C． D． C　[∵AB的中点M，‎ ‎∴＝，故|CM|＝||‎ ‎＝ ＝.]‎ ‎3．已知a＝(x,1,2)，b＝(1,2，－y)，且(‎2a＋b)∥(－a＋2b)，则(　　) ‎ ‎【导学号：46342157】‎ A．x＝，y＝1 B．x＝，y＝－4‎ C．x＝2，y＝－ D．x＝1，y＝－1‎ B　[‎2a＋b＝(2x＋1,4,4－y)，－a＋2b＝(2－x,3，－2y－2)，∵(‎2a＋b)∥(－a＋2b)，则存在非零实数λ，使得‎2a＋b＝λ(－a＋2b)，∴∴.]‎ ‎4．已知向量a＝(－2，x,2)，b＝(2,1,2)，c＝(4，－2,1)，若a⊥(b－c)，则x的值为(　　)‎ A．－2 B．2‎ C．3 D．－3‎ A　[∵b－c＝(－2,3,1)，a·(b－c)＝4＋3x＋2＝0，∴x＝－2.]‎ ‎5．已知a＋b＝(2，，2)，a－b＝(0，，0)，则cos〈a，b〉＝(　　)‎ A． B． C． D． 6‎ C　[由已知，得a＝(1，，)，b＝(1,0，)，∴cos〈a，b〉＝＝＝.]‎ 二、填空题 ‎6．已知a＝(1,1,0)，b＝(0,1,1)，c＝(1,0,1)，p＝a－b，q＝a＋2b－c，则p·q＝________.‎ ‎－1　[∵p＝a－b＝(1,0，－1)，q＝a＋2b－c＝(0,3,1)，‎ ‎∴p·q＝1×0＋0×3＋(－1)×1＝－1.]‎ ‎7．已知a＝(cos α，1，sin α)，b＝(sin α，1，cos α)，则向量a＋b与a－b的夹角是________. ‎ ‎【导学号：46342158】‎ ‎90°　[a＋b＝(cos α＋sin α，2，sin α＋cos α)，a－b＝(cos α－sin α，0，sin α－cos α)，∴(a＋b)·(a－b)＝0，‎ ‎∴(a＋b)⊥(a－b)．]‎ ‎8．已知点A(1,2,3)，B(2,1,2)，P(1,1,2)，O(0,0,0)，点Q在直线OP上运动，当·取得最小值时，点Q的坐标为________．‎ 　[设＝λ＝(λ，λ，2λ)，故Q(λ，λ，2λ)，故＝(1－λ，2－λ，3－2λ)，＝(2－λ，1－λ，2－2λ)．‎ 则·＝6λ2－16λ＋10＝62－，当·取最小值时，λ＝，此时Q点的坐标为.]‎ 三、解答题 ‎9．如图3140，已知四棱台ABCDA1B‎1C1D1的上、下底面分别是边长为3和6的正方形，A‎1A＝6，且A‎1A⊥底面ABCD．点P，Q分别在棱DD1，BC上．若P是DD1的中点，证明：AB1⊥PQ.‎ 图3140‎ 6‎ ‎[解]　由题设知，AA1，AB，AD两两垂直．以A为坐标原点，分别以，，为正交基底建立如图所示的空间直角坐标系，则A(0,0,0)，B1(3,0,6)，D(0,6,0)，D1(0,3,6)．设Q(6，m,0)，其中m＝BQ,0≤m≤6.‎ 若P是DD1的中点，则P，＝.又＝(3,0,6)，于是·＝18－18＝0，所以⊥，即AB1⊥PQ.‎ ‎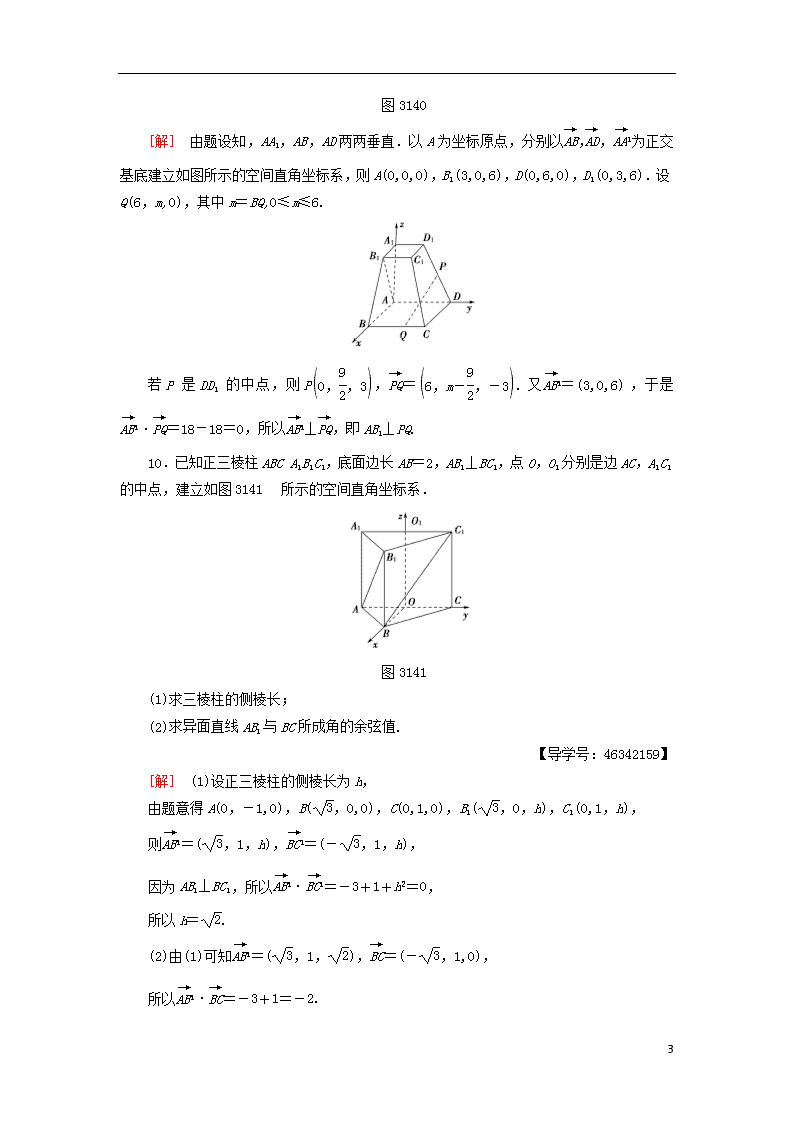10．已知正三棱柱ABCA1B‎1C1，底面边长AB＝2，AB1⊥BC1，点O，O1分别是边AC，A‎1C1的中点，建立如图3141所示的空间直角坐标系．‎ 图3141‎ ‎(1)求三棱柱的侧棱长；‎ ‎(2)求异面直线AB1与BC所成角的余弦值. ‎ ‎【导学号：46342159】‎ ‎[解]　(1)设正三棱柱的侧棱长为h，‎ 由题意得A(0，－1,0)，B(，0,0)，C(0,1,0)，B1(，0，h)，C1(0,1，h)，‎ 则＝(，1，h)，＝(－，1，h)，‎ 因为AB1⊥BC1，所以·＝－3＋1＋h2＝0，‎ 所以h＝.‎ ‎(2)由(1)可知＝(，1，)，＝(－，1,0)，‎ 所以·＝－3＋1＝－2.‎ 6‎ 因为||＝，||＝2，所以cos〈，〉＝＝－.‎ 所以异面直线AB1与BC所成角的余弦值为.‎ ‎[能力提升练]‎ ‎1．已知A(1,2，－1)，B(5,6,7)，则直线AB与平面xOz交点的坐标是(　　)‎ A．(0,1,1) B．(0,1，－3)‎ C．(－1,0,3) D．(－1,0，－5)‎ D　[设直线AB与平面xOz交点的坐标是M(x,0，z)，则＝(x－1，－2，z＋1)．又＝(4,4,8)，与共线，∴＝λ，即，解得x＝－1，z＝－5，‎ ‎∴点M的坐标为(－1,0，－5)．故选D．]‎ ‎2．直三棱柱ABCA1B‎1C1中，∠BCA＝90°，M，N分别是A1B1，A‎1C1的中点，BC＝CA＝CC1，则BM与AN所成角的余弦值为(　　)‎ A．　 B．　　　C．　　　D． C　[建立如图所示的空间直角坐标系Cxyz，设BC＝2，则B(0,2,0)，A(2,0,0)，M(1,1,2)，N(1,0,2)，所以＝(1，－1,2)，＝(－1,0,2)，故BM与AN所成角θ的余弦值cos θ＝＝＝.]‎ ‎3．如图3142，在三棱锥VABC中，顶点C在空间直角坐标系的原点处，顶点A，B，V分别在x，y，z轴上，D是线段AB的中点，且AC＝BC＝2，当∠VDC＝60°时，异面直线AC与VD所成角的余弦值为________．‎ 6‎ 图3142‎ 　[由题意，A(2,0,0)，B(0,2,0)，C(0,0,0)，D(1,1,0)，当∠VDC＝60°时，在Rt△VCD中，CD＝，VC＝，VD＝2，∴V(0,0，)，∴＝(－2,0,0)，＝(1,1，－)，∴cos〈，〉＝＝－，∴异面直线AC与VD所成角的余弦值为.]‎ ‎4．设向量a＝(1，－2,2)，b＝(－3，x,4)，已知a在b上的投影为1，则x＝________.‎ ‎0　[∵a在b上的投影为1，∴|a|·cos〈a，b〉＝1，∴a·b＝|a|·|b|·cos〈a，b〉＝|b|，∴－3－2x＋8＝，解得x＝0或x＝(舍去)．]‎ ‎5．如图3143，四棱锥PABCD中，PA⊥底面ABCD，BC＝CD＝2，AC＝4，∠ACB＝∠ACD＝，F为PC的中点，AF⊥PB．求PA的长. ‎ ‎【导学号：46342160】‎ 图3143‎ ‎[解]　如图，连接BD交AC于O，因为BC＝CD，即△BCD为等腰三角形，又AC平分∠BCD，故AC⊥BD．以O为坐标原点，分别以，，为正交基底建立空间直角坐标系Oxyz.‎ 6‎ 因为OC＝CDcos ＝1，AC＝4，所以AO＝AC－OC＝3，又OB＝OD＝CDsin ＝，故A(0，－3,0)，B(，0,0)，C(0,1,0)，D(－，0,0)．‎ 由PA⊥底面ABCD，可设P(0，－3，z)，其中z>0.‎ 由F为PC的中点，得F，所以＝，＝(，3，－z)．‎ 又AF⊥PB，所以·＝0，即6－＝0，解得z＝2或z＝－2(舍去)．所以＝(0,0，－2)，则||＝2.‎ 所以PA的长为2.‎ 6‎