高考数学模拟试卷3 (3) 12页

- 1 - 2018 年春季湖北省重点高中联考协作体期中考试 高三数学理科试卷(39) 第Ⅰ卷（选择题 共 60 分） 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1.在复平面内，复数 z 满足 (1 ) 2z i  ，则 z 的共轭复数对应的点位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 2.已知集合 { 1 2}M x x   ，集合 { ( 1)( 3) 0}N x Z x x     ，则 M N  （ ） A．{0,1,2} B．{ 1,0,1,2} C．{ 1,0,2,3} D．{0,1,2,3} 3.根据如下样本数据： x 3 5 7 9 y 6 a 3 2 得到回归方程 ^ 1.4 12.4y x   ，则（ ） A．变量 x 与 y 之间是函数关系 B．变量 x 与 y 线性正相关 C．线性回归直线经过上述各样本点 D． 5a  4.《张丘建算经》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有女不善织， 日减功迟，初日织五尺，末日织一尺，今三十织迄，问织几何.”其意思为:有个女子不善于 织布，每天比前一天少织同样多的布，第一天织五尺，最后一天织一尺，三十天织完，问三 十天共织布（ ） A．30 尺 B．150 尺 C. 90 尺 D．180 尺 5.已知实数 ,x y 满足 1 1 0 2 1 x y x x y         ，则目标函数 4 2Z x y  的最大值等于（ ） A．-14 B．-5 C. 4 D．6 6. 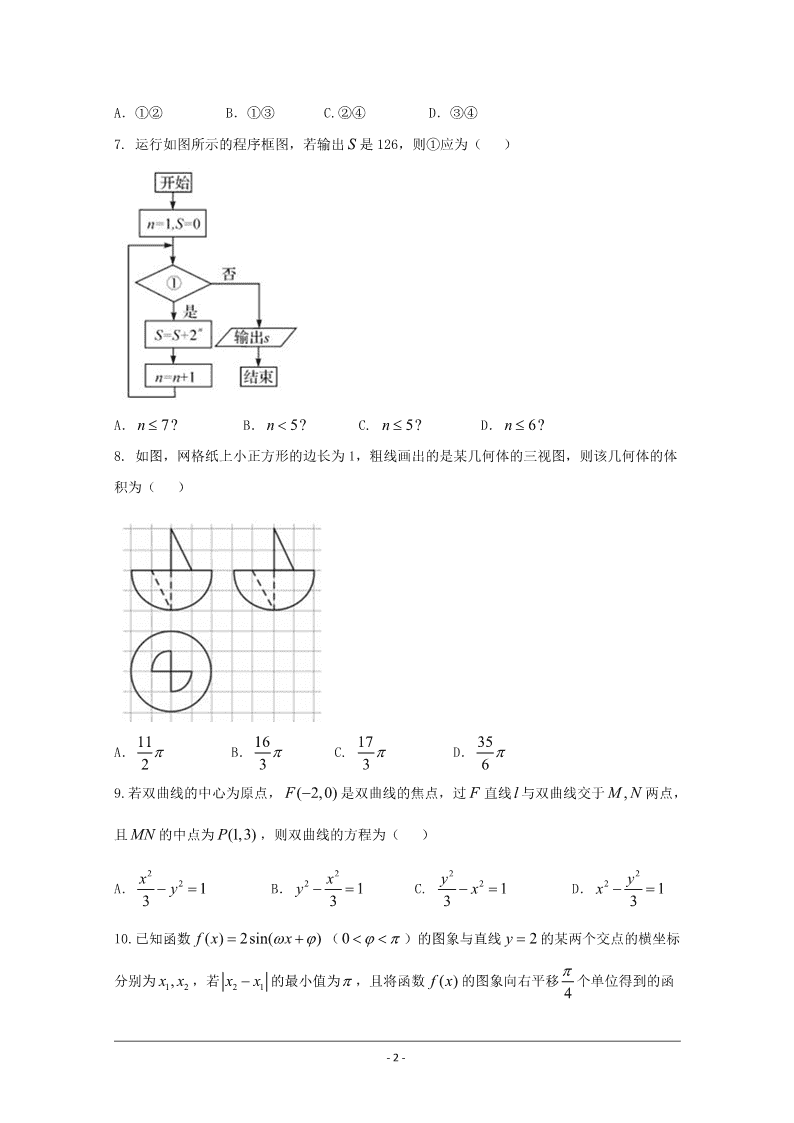已知直线 ,l m ，平面 ,  ，且l  ， m  ，下列命题：① // l m    ；② //l m   ③ //l m    ；④ //l m    其中正确的序号是（ ） - 2 - A．①② B．①③ C.②④ D．③④ 7. 运行如图所示的程序框图，若输出 S 是 126，则①应为（ ） A． 7?n  B． 5?n  C. 5?n  D． 6?n  8. 如图，网格纸上小正方形的边长为 1，粗线画出的是某几何体的三视图，则该几何体的体 积为（ ） A．11 2  B．16 3  C. 17 3  D． 35 6  9.若双曲线的中心为原点， ( 2,0)F  是双曲线的焦点，过 F 直线l 与双曲线交于 ,M N 两点， 且 MN 的中点为 (1,3)P ，则双曲线的方程为（ ） A． 2 2 13 x y  B． 2 2 13 xy   C. 2 2 13 y x  D． 2 2 13 yx   10.已知函数 ( ) 2sin( )f x x   （ 0    ）的图象与直线 2y  的某两个交点的横坐标 分别为 1 2,x x ，若 2 1x x 的最小值为 ，且将函数 ( )f x 的图象向右平移 4  个单位得到的函 - 3 - 数为奇函数，则函数 ( )f x 的一个递增区间为（ ） A． ( ,0)2  B． ( , )4 4   C. (0, )2  D． 3( , )4 4   11. 已知点 1F 是抛物线 2 4x y 的焦点，点 2F 为抛物线的对称轴与其准线的交点，过 2F 作抛 物线的切线，切点为 A ，若点 A 恰在以 1 2,F F 为焦点的双曲线上，则双曲线的离心离为（ ） A． 6 2 2  B． 2 1 C. 6 2 2  D． 2 1 12.已知函数 ( )f x 是 R 上的奇函数，当 0x  时， 1 12 ,0 2 ( ) 1 ( 2), 22 x x f x f x x        ，则函数 ( ) ( ) 1g x xf x  在[ 7, )  上的所有零点之和为（ ） A．0 B．4 C.8 D．16 第Ⅱ卷（非选择题 共 90 分） 二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上） 13.在 ABC 中， AB AC AB AC      ， 3AB  ，则 AB BC   ． 14.已知 0a  ， 4(1 ) ( 2)ax x  的展开式中 2x 项的系数为 1，则 a 的值为 ． 15.已知各项都为正数的数列{ }na ，对任意的 *,m n N ， m n m na a a   恒成立，且 3 5 4 72a a a   ，则 2 1 2 2 2 7log log loga a a    ． 16.若以曲线 ( )y f x 上任意一点 ( , )M x y 为切点作切线l ，曲线上总存在异于 M 的点 1 1( , )N x y ，以点 N 为切点作线 1l ，且 1//l l ，则称曲线 ( )y f x 具有“可平行性”，下列曲线 具有可平行性的编号为 ．（写出所有的满足条件的函数的编号） ① 1y x  ② 3y x x  ③ cosy x ④ 2( 2) lny x x   三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.） 17.在 ABC 中，设内角 , ,A B C 的对边分别为 , ,a b c ，且 2sin( ) sin( )4 4 2C C     . （1）求角C ； （2）若 3 3c  且sin 2sinA B ，求 ABC 的面积. - 4 - 18.从某校高中男生中随机选取 100 名学生，将他们的体重（单位： kg ）数据绘制成频率分 布直方图，如图所示. （1）估计该校的 100 名同学的平均体重（同一组数据以该组区间的中点值作代表）； （2）若要从体重在[60,70) ，[70,80) 内的两组男生中，用分层抽样的方法选取 5 人，再从这 5 人中随机抽取 3 人，记体重在[60,70) 内的人数为 ，求其分布列和数学期望 ( )E  . 19.等边 ABC 的边长为 3，点 ,E F 分别为 ,AB BC 上的点，且满足 1 2 AD CE DB EA   （如图 1）， 将 ADE 沿 DE 折起到 1A DE 的位置，使二面角 1A DE B  成直二面角，连接 1A B ， 1AC （如图 2） （1）求证： 1A D  平面 BCED ； （2）在线段 BC 上是否存在点 P ，使直线 1PA 与平面 1A BD 所成的角为 060 ？若存在，求出 PB 的长；若不存在，请说明理由. 20.在平面直角坐标系 xOy 中，点 1( 3,0)F  ，圆 2 2 2 : 2 3 13 0F x y x    ，点Q 是圆上 一动点，线段 1FQ 的中垂线与线段 2F Q 交于点 P . - 5 - （1）求动点 P 的轨迹 E 的方程； （2）若直线l 与曲线 E 相交于 ,A B 两点，且存在点 (4,0)D （其中 , ,A B D 不共线），使得 ADB 被 x 轴平分，证明：直线l 过定点. 21.已知函数 2( ) ( ) xf x ax x a e    ( )a R . （1）若 0a  ，函数 ( )f x 的极大值为 5 e ，求实数 a 的值； （2）若对任意的 0a  ， ( ) ln( 1)f x b x  ，在 [0, )x  上恒成立，求实数b 的取值范围. 请考生在 22、23 两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修 4-4：坐标系与参数方程 已知曲线 C 的参数方程为 cos 1 sin x y       ，其中 为参数，且 [0, ]  在直角坐标系 xOy 中， 以坐标原点O 为极点，以 x 轴正半轴为极轴建立极坐标系. （1）求曲线C 的极坐标方程； （2）设T 是曲线C 上的一点，直线OT 被曲线C 截得的弦长为 3 ，求T 点的极坐标. 23.选修 4-5：不等式选讲 已知函数 ( )f x x x a  ， a R （1）求 (1) ( 1) 1f f   ，求 a 的取值范围； （2）若 0a  ，对 , ( , ]x y a   ，都有不等式 5( ) 4f x y y a    恒成立，求 a 的取值 范围. - 6 - 2018 年春季湖北省重点高中联考协作体期中考试 高三数学试卷（理科）参考答案(39) 一、选择题：DADCC BDBDA BC 二、填空题：13.-9 14. 6 1 15.21 16.①③ 三、解答题: 17. 解:(1) )4cos(42sin)4sin( CCC            故由已知可得: 2 2)4sin()4cos(  CC  即 2 1cos2 2)2sin(2  CC 又 30   CC 由 BA sin2sin  及正弦定理得: ba 2 (2) 由(1) 3 C 又 33c 故由余弦定理得: 3cos)2(2)2()33( 222 bbbb  解得: 3b 从而 6a 2 39 2 3362 1sin2 1   CabS ABC 18．解：(1)依频率分布直方图得各组的频率依次为： 10.0,20.0,30.0,35.0,05.0 故估计 100 名学生的平均体重约为: 5.6410.08520.07530.06535.05505.045  (2) 由 (1) 及 已 知 可 得 ： 体 重 在    807070,60 ，及 的 男 生 分 别 为 ： 0.30 100=30 （人） 0.20 100=20 （人） 从中用分层抽样的方法选 5 人，则体重在 60,70 内的应选 3 人，体 重在 70,80 内的应选 2 人 从 而  的 可 能 取 值 为 1 ， 2 ， 3 且 得 ：   10 31 3 5 1 3  C CP    5 32 3 5 2 3 1 2  C CCP  - 7 -   10 13 3 5 3 3  C CP  其分布列为： P 1 2 3  10 3 5 3 10 1 故得： 8.110 135 3210 31)( E 18. 解：（1）证明： 如图 1，由已知可得： 60,1,2  AADAE 从而 360cos21221 22  DE 故得 222 AEDEAD  DEBDDEAD  , 即图 2 中： DEBDDEDA  ,1 DBA1 为二面角 BDEA 1 的平面角 而二面角 BDEA 1 为直二面角， 901  DBA 即 DBDA 1 BCED, 平面且  DBDEDDBDE  BCEDDA 平面 1 （2）由（1） DEDBDA ,,1 两两垂直，分别以 轴所在直线为 zyxDADEDB ,,,, 1 建立空间直 角坐标系，则由已知及（1）可得： )0,2 33,2 1(),1,0,0(),0,0,2(),0,0,0( 1 CABD 令 )10(   BCBP 则因 )0,0,2(),0,2 33,2 3(   DBBC 故 )0,2 33,2 32()0,2 33,2 3()0,0,2(    BCDBBPDBDP - 8 - 即 )0,2 33,2 32( P 由（1）知 )0,1,0(  n 为平面 BDA1 的一个法向量 又 )1,2 33,2 32(1   AP 若存在满足条件的 P，则 2 360sin,cos 1   PAn 即 2 3 )1()2 33()2 32( 2 33 222     解得 6 5 而 2 5,3   BCBPBC  故存在满足条件的点 P，且 PB 的长为 2 5 19. （1）由已知 )0,3(1 F ， )0,3(2F ，圆 2F 的半径为 4r 依题意有： PQPF 1 42221  rQFPFPQPFPF 故点 P 的轨迹是以 21, FF 为焦点，长轴长为 4 的椭圆，即 1,2,3  bac 故点 P 的轨迹 E 的方程为 14 2 2  yx （2）令 ),(),,( 2211 yxByxA ，因 A，B，D 不共线，故l 的斜率不为 0，可令l 的方程为： nmyx  ， 则由  nmyx yx   44 22 得 042)4( 222  nmnyym 则 4 4,4 2 2 2 21221    m nyym mnyy ① ADB 被 x 轴平分， 0 DBDA kk 即 044 2 2 1 1  x y x y 亦即 0)(4 211221  yyxyxy ② 而 )(2)()( 212112211221 yynymynmyynmyyxyxy  代入②得： - 9 - 0))(4(2 2121  yynymy ③ ①代入③得： m2 )4 4( 2 2   m n 0)4 2)(4( 2   m mnn 0m 时得： 1n 此时 l 的方程为： 1 myx 过定点（1，0） 0m 时 ， 1n 亦满足 此时l 的方程为： 1x 综上所述，直线l 恒过定点（1，0） 21.解：（1）由题意， . ①当 时， ， 令 ，得 ； ，得 ， 所以 )(xf 在 )1,( 单调递增 ),1(  单调递减. 所以 )(xf 的极大值为 eef 51)1(  ，不合题意. ②当 时， ， 令 ，得 ； ，得 或 ， 所以 )(xf 在 )1,11( a  单调递增， )11,( a  ， ),1(  单调递减. 所以 )(xf 的极大值为 ee af 512)1(  ，得 2a . 综上所述 2a . （2）令 ， 当 时， ， 故  0-)( ，于 ag 上递增， )0(,)0()(   xxegag x 原问题    ,0)1ln( xxbxe x 于 上恒成立 - 10 - ①当 时， ， ， ， 此时 ，不合题意. ②当 时，令 ， ， 则 ，其中 ， ， 令 ，则 )(xp 在区间 ,0 上单调递增 （ⅰ） 时， ， 所以对 ， ，从而 在 上单调递增， 所以对任意 ， ， 即不等式 在 上恒成立. （ⅱ） 时，由 ， 及 在区间 上单调递增， 所以存在唯一的 使得 ，且 时， . 从而 时， ，所以 在区间 上单调递减， 则 时， ，即 ，不符合题意. 综上所述， . 22.解: （Ⅰ）根据曲线 的参数方程得 曲线 C 的普通方程为： 2 2（x-1） 1y  曲线 的极坐标方程为： 2 cos ( 0, )2          （Ⅱ）由题得 3OT ， - 11 - 所以令 3 2 cos  ， 0, 2       ，则解得 6   . 故点 的极坐标为 ( 3, )6  23. 解:(1)由 Raaxxxf  ,)( 得 1111)1()1(  aaff  1 1)1()1(   a aa 或 11 1)1()1(   a aa 或 1 1)1()1(   a aa  aaa 或或 2 111 2 1 a 综上所述, )2 1,( a (2) 当   )0(,  aay 时,记 ayyyg  4 5)( 则 )4 5(,4 5 4 5 4 5)(  时取ayaayayyg 即 ayg  4 5)( 的最小值为 当   )0(,  aax 4)2()()( 2 2 aaxxaxxf  2 ax  时 )(xf 的最大值为 4 2a 故原问题 510544 5 4 2 2  aaaaa 又  5,00  aa - 12 -