浙江省2021届高考数学一轮复习第八章立体几何与空间向量加强练八立体几何与空间向量含解析 13页

加强练(八)　立体几何与空间向量 一、选择题(本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1.(2015·上海卷)如图，四个棱长为1的正方体排成一个正四棱柱，AB是一条侧棱，Pi(i＝1，2，…，8)是上底面上其余八个点，则·(i＝1，2，…，8)的不同值的个数为(　　)‎ A.1 B.2 ‎ C.4 D.8‎ 解析　∵·＝||·||cos〈，〉＝1×1＝1，∴只有一个值.‎ 答案　A ‎2.(2020·宁波模拟)若直线l不平行于平面α，且l⊄α，则(　　)‎ A.α内所有直线与l异面 B.α内只存在有限条直线与l共面 C.α内存在唯一的直线与l平行 D.α内存在无数条直线与l相交 解析　由直线与平面的位置关系知l⊄α，则l∥α或l与平面α相交.由题意知，l不平行于平面α，则设l∩α＝P，故平面α内所有过点P的直线与l相交，平面α内不过点P的直线与l异面，故选D.‎ 答案　D ‎3.如图，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB＝30°，则点P的轨迹是(　　)‎ A.直线 B.抛物线 C.椭圆 D.双曲线的一支 解析　利用平面截圆锥面直接得轨迹.因为∠PAB＝30°，所以点P的轨迹为以AB为轴线，PA为母线的圆锥面与平面α的交线，且平面α与圆锥的轴线斜交，故点P的轨迹为椭圆.‎ 答案　C ‎4.(2017·浙江卷)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是(　　)‎ A.＋1 B.＋3 ‎ C.＋1 D.＋3‎ 解析　由几何体的三视图可知，该几何体是一个底面半径为1，高为3的圆锥的一半与一个底面为直角边长是的等腰直角三角形，高为3的三棱锥的组合体，所以该几何体的体积V＝×π×12×3＋××××3＝＋1.‎ 答案　A ‎5.已知正方体ABCD－A1B1C1D1的棱长为，正方体所在空间的动点P满足|＋|＝2，则·的取值范围是(　　)‎ A.[0，4] B.[1，4]‎ C.[0，2] D.[1，2]‎ 解析　因为正方体的棱长为，所以B1C＝2，则由|＋|＝2得点P在以B1C的中点为球心，为半径的球面上.当点P与点B重合时，点P在直线AD1上的射影为点A，当点P与点C1重合时，点P在直线AD1上的射影为点D1，则·∈[0，||2]＝[0，4]，故选A.‎ 答案　A ‎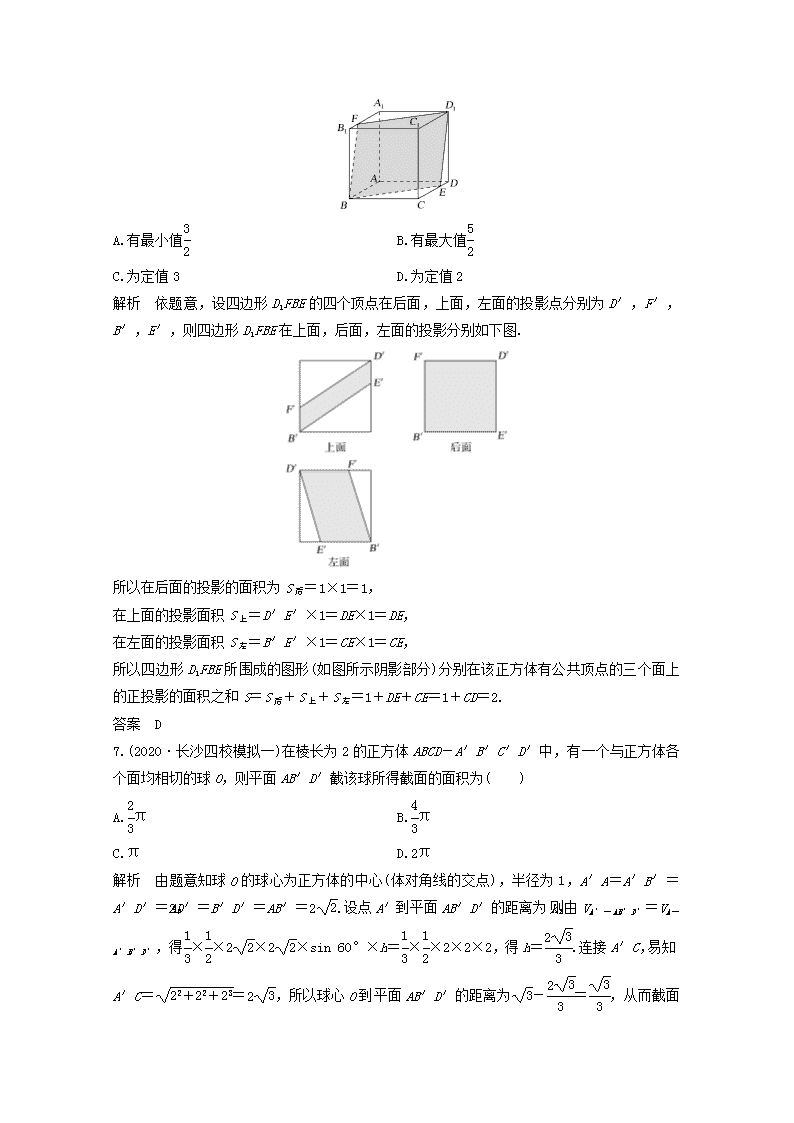6.(2020·北京朝阳区模拟)在棱长为1的正方体ABCD－A1B1C1D1中，E，F分别为线段CD和A1B1上的动点，且满足CE＝A1F，则四边形D1FBE所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和(　　)‎ A.有最小值 B.有最大值 C.为定值3 D.为定值2‎ 解析　依题意，设四边形D1FBE的四个顶点在后面，上面，左面的投影点分别为D′，F′，B′，E′，则四边形D1FBE在上面，后面，左面的投影分别如下图.‎ 所以在后面的投影的面积为S后＝1×1＝1，‎ 在上面的投影面积S上＝D′E′×1＝DE×1＝DE，‎ 在左面的投影面积S左＝B′E′×1＝CE×1＝CE，‎ 所以四边形D1FBE所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和S＝S后＋S上＋S左＝1＋DE＋CE＝1＋CD＝2.‎ 答案　D ‎7.(2020·长沙四校模拟一)在棱长为2的正方体ABCD－A′B′C′D′中，有一个与正方体各个面均相切的球O，则平面AB′D′截该球所得截面的面积为(　　)‎ A.π B.π ‎ C.π D.2π 解析　由题意知球O的球心为正方体的中心(体对角线的交点)，半径为1，A′A＝A′B′＝A′D′＝2，AD′＝B′D′＝AB′＝2.设点A′到平面AB′D′的距离为h，则由VA′－AB′D′＝VA－A′B′D′，得××2×2×sin 60°×h＝××2×2×2，得h＝.连接A′C，易知A′C＝＝2，所以球心O到平面AB′D′的距离为－＝，从而截面圆的半径为＝ ‎，因此所求截面的面积为π.‎ 答案　A ‎8.(2020·北京西城区综合练习)已知正方体ABCD－A1B1C1D1的棱长为1，平面α与此正方体相交.对于实数d(0＜d＜)，如果正方体ABCD－A1B1C1D1的八个顶点中恰好有m个点到平面α的距离等于d，那么下列结论中一定正确的是(　　)‎ A.m≠6 B.m≠5 ‎ C.m≠4 D.m≠3‎ 解析　如图(1)恰好有3个点到平面α的距离为d；如图(2)恰好有4个点到平面α的距离为d；如图(3)恰好有6个点到平面α的距离为d.‎ 答案　B ‎9.(2020·浙江名师预测卷二)如图，已知三棱锥S－ABC中，SA＝SB＝SC，∠ABC＝90°，AB＞BC，E，F，G分别是AB，BC，AC的中点，分别记平面SEF与平面SAC、平面SEG与平面SBC、平面SFG与平面SAB所成的锐二面角为α，β，γ，则α，β，γ的大小关系是(　　)‎ A.α＜β＜γ B.β＜α＜γ C.α＜γ＜β D.γ＜β＜α 解析　由SA＝SB＝SC可知点S在底面ABC上的射影是△ABC的外心，∵∠ABC＝90°，∴AC的中点G就是点S在底面ABC上的射影，即SG⊥平面ABC，过点G作GH⊥EF，交EF于点H，连接SH，则∠GSH就是平面SEF与平面SAC所成角的平面角，tan∠GSH＝tan α＝，易证GF⊥平面SEG，∴∠GSF就是平面SEG与平面SBC所成角的平面角，tan∠GSF＝tan β＝，同理，tan∠GSE＝tan γ＝，在Rt△EGF中，GH＜GE＜GF，∴tan α＜tan γ＜tan β，∴α＜γ＜β，故选C.‎ 答案　C ‎10.如图，已知平面α⊥β，α∩β＝l，A、B是直线l上的两点，C、D是平面β 内的两点，且DA⊥l，CB⊥l，AD＝3，AB＝6，CB＝6.P是平面α上的一动点，且直线PD，PC与平面α所成角相等，则二面角P－BC－D的余弦值的最小值是(　　)‎ A. B. ‎ C. D.1‎ 解析　∵DA⊥l，α∩β＝l，α⊥β，AD⊂β，∴AD⊥α，同理，BC⊥α.∴∠DPA为直线PD与平面α所成的角，∠CPB为直线PC与平面α所成的角，∴∠DPA＝∠CPB，又∠DAP＝∠CBP＝90°，∴△DAP∽△CBP，∴＝＝.在平面α内，以AB为x轴，以AB的中垂线为y轴建立平面直角坐标系，则A(－3，0)，B(3，0).设P(x，y)，(y＞0)，∴2＝，整理得(x＋5)2＋y2＝16.∴P点在平面α内的轨迹为以M(－5，0)为圆心，以4为半径的上半圆.∵平面PBC∩平面β＝BC，PB⊥BC，AB⊥BC，∴∠PBA为二面角P－BC－D的平面角.∴当PB与圆相切时，∠PBA最大，cos∠PBA取得最小值.此时PM＝4，MB＝8，MP⊥PB，∴PB＝4，cos∠PBA＝＝＝.‎ 答案　C 二、填空题(本大题共7小题，多空题每题6分，单空题每题4分，共36分)‎ ‎11.(2019·全国Ⅰ卷)已知∠ACB＝90°，P为平面ABC外一点，PC＝2，点P到∠ACB两边AC，BC的距离均为，那么P到平面ABC的距离为________.‎ 解析　如图，过点P作PO⊥平面ABC于O，则PO为P到平面ABC的距离.‎ 再过O作OE⊥AC于E，OF⊥BC于F，‎ 连接OC，PE，PF，则PE⊥AC，PF⊥BC.‎ 所以PE＝PF＝，所以OE＝OF，‎ 所以CO为∠ACB的平分线，‎ 即∠ACO＝45°.‎ 在Rt△PEC中，PC＝2，PE＝，所以CE＝1，‎ 所以OE＝1，所以PO＝＝＝.‎ 答案　 ‎12.如图，正方体ABCD－A1B1C1D1的棱长为4，P为BC的中点，Q为线段CC1上的动点(异于C点)，过点A，P，Q的平面截该正方体所得的截面记为M.‎ 当CQ＝________时(用数值表示)，M为等腰梯形；‎ 当CQ＝4时，M的面积为________.‎ 解析　连接AP并延长交DC的延长线于点N，当点Q为CC1的中点，即CQ＝2时，连接D1N，则D1N过点Q，PQ綉AD1，显然AP＝D1Q，M为等腰梯形；当CQ＝4时，NQ交棱DD1延长线上一点(设为G)，且GD1＝4，AG过A1D1的中点，此时M为菱形，其对角线长分别为4和4，故其面积为8.‎ 答案　2　8 ‎13.(2020·浙江“超级全能生”联考)某几何体的三视图(单位：cm)如图所示，则该几何体的体积是________ cm3，表面积是________ cm2.‎ 解析　易知该几何体是一个底面为直角梯形，一条侧棱垂直底面的四棱锥，所以该几何体的体积V＝××4＝16(cm3)，表面积为＋＋＋＋＝8＋4＋24(cm2).‎ 答案　16　8＋4＋24‎ ‎14.(2020·北仑中学模拟)如图，正四面体ABCD的棱CD在平面α内，E为棱BC的中点，当正四面体ABCD绕CD旋转时，直线AE与平面α所成最大角的正弦值为________.‎ 解析　过点E作CD的平行线，交BD于F，则正四面体绕CD旋转时AE与平面α所成角相当于绕EF旋转时AE与平面α所成角.此时直线AE形成一个圆锥，所以可知直线AE与平面α所成角的最大值即为AE与EF所成的角.设正四面体的棱长为2，则AE＝AF＝，EF＝1，所以cos∠AEF＝＝，所以sin∠AEF＝，即直线AE与平面α所成最大角的正弦值为.‎ 答案　 ‎15.已知球O与棱长为4的正方体ABCD－A1B1C1D1的所有棱都相切，点M是球O上一点，点N是△ACB1的外接圆上一点，则线段MN长度的最大值为________；最小值为________.‎ 解析　因为球O与棱长为4的正方体的各棱都相切，所以球O的半径为2，球心O在体对角线的中点，△ACB1的外接圆是正方体外接球的一个小圆，点N是△ACB1的外接圆上一点，则点N到球心O的距离为2(即正方体外接球的半径)，因为点M是球O上一点，所以线段MN长度的最小值为2－2，线段MN长度的最大值为2＋2.‎ 答案　2＋2　2－2 ‎16.(2020·绍兴一中适应性考试)已知半径为4的球面上有两点A，B，AB＝4，球心为O，若球面上的动点C满足二面角C－AB－O的大小为60°，则四面体OABC的外接球的半径为________.‎ 解析　如图，由已知，AO⊥OB，又平面ABC与平面AOB所成的二面角大小为60°，则平面ABC截球O的球面为一个圆，当点C在弧ACB的中点时，取AB的中点M，连接CM，OM，则AB⊥平面CMO，故二面角C－AB－O的平面角为∠CMO，则∠CMO＝60°.作OH⊥CM于点H，由OA＝OB＝OC＝4，AB＝4，设四面体OABC的外接球球心为O1∈OH，则由OM＝AB＝2得OH＝OMsin 60°＝.HM＝OMcos 60°＝，故四面体OABC的外接球的半径r满足O1O2＝O1A2＝HM2＋AM2＋O1H2，即r2＝()2＋(2)2＋(r－)2，解得r＝.‎ 答案　 ‎17.(2019·全国Ⅱ卷)中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图①).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图②是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1，则该半正多面体共有________个面，其棱长为________.‎ 解析　依题意知，题中的半正多面体的上、下、左、右、前、后6个面都在正方体的表面上，且该半正多面体的表面由18个正方形，8个正三角形组成，因此题中的半正多面体共有26个面.注意到该半正多面体的俯视图的轮廓是一个正八边形，设题中的半正多面体的棱长为x ‎，则 x＋x＋x＝1，解得x＝－1，故题中的半正多面体的棱长为－1.‎ 答案　26　－1‎ 三、解答题(本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤)‎ ‎18.(本小题满分14分)如图，在直三棱柱ABC－A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.求证：‎ ‎(1)直线DE∥平面A1C1F；‎ ‎(2)平面B1DE⊥平面A1C1F.‎ 证明　(1)在直三棱柱ABC－A1B1C1中，A1C1∥AC.‎ 在△ABC中，因为D，E分别为AB，BC的中点，‎ 所以DE∥AC，于是DE∥A1C1.‎ 又因为DE⊄平面A1C1F，A1C1⊂平面A1C1F，‎ 所以直线DE∥平面A1C1F.‎ ‎(2)在直三棱柱ABC－A1B1C1中，A1A⊥平面A1B1C1.‎ 因为A1C1⊂平面A1B1C1，所以A1A⊥A1C1.‎ 又因为A1C1⊥A1B1，A1A⊂平面ABB1A1，A1B1⊂平面ABB1A1，A1A∩A1B1＝A1，‎ 所以A1C1⊥平面ABB1A1.‎ 因为B1D⊂平面ABB1A1，‎ 所以A1C1⊥B1D.‎ 又因为B1D⊥A1F，A1C1⊂平面A1C1F，A1F⊂平面A1C1F，A1C1∩A1F＝A1，‎ 所以B1D⊥平面A1C1F.‎ 因为直线B1D⊂平面B1DE，‎ 所以平面B1DE⊥平面A1C1F.‎ ‎19.(本小题满分15分)(2020·嘉、丽、衢模拟)如图，在矩形ABCD中，AB＝4，AD＝3，点E，F分别是线段DC，BC的中点，分别将△DAE沿AE折起，△CEF沿EF折起，使得D，C重合于点G，连接AF.‎ ‎(1)求证：平面GEF⊥平面GAF；‎ ‎(2)求直线GF与平面GAE所成角的正弦值.‎ ‎(1)证明　因为EG⊥AG，EG⊥FG，GA∩GF＝G，‎ 所以GE⊥平面GAF，又GE⊂平面GEF，‎ 所以平面GEF⊥平面GAF.‎ ‎(2)解　过F作FH⊥AG于H，‎ 则由GE⊥平面GAF，且FH⊂平面GAF知，‎ GE⊥FH，GA∩GE＝G，所以FH⊥平面GAE，‎ 从而∠FGH是直线GF与平面GAE所成角.‎ 因为GA＝3，GF＝，AF＝＝，‎ 所以cos∠AGF＝＝＝－，‎ 从而sin∠FGH＝sin∠AGF＝＝.‎ 所以直线GF与平面GAE所成角的正弦值为.‎ ‎20.(本小题满分15分)(2020·浙江教育绿色评价联盟适考)如图，圆的直径AC＝2，B为圆周上不与点A，C重合的点，PA垂直于圆所在的平面，∠PCA＝45°.‎ ‎(1)求证：PB⊥BC；‎ ‎(2)(一题多解)若BC＝，求二面角B－PC－A的余弦值.‎ ‎(1)证明　如图，连接AB，‎ 因为PA⊥平面ABC，‎ 所以PA⊥BC.‎ 又因为B在圆周上，‎ 所以AB⊥BC，PA∩AB＝A，‎ 故BC⊥平面PAB.又PB⊂平面PAB，‎ 故BC⊥PB.‎ ‎(2)解　法一　过B作AC的垂线，垂足为D，‎ 则BD⊥平面PAC，因为PC⊂平面PAC，故BD⊥PC.‎ 再过D作PC的垂线，垂足为E，‎ 则PC⊥DE，因为BD∩DE＝D，‎ 所以PC⊥平面BDE，又BE⊂平面BDE，故BE⊥PC，‎ 可知∠BED即为二面角B－PC－A的平面角.‎ 因为BC＝，所以BD＝，CD＝.‎ 又因为∠PCA＝45°，所以DE＝，BE＝，‎ 所以cos∠BED＝＝.‎ 即二面角B－PC－A的余弦值为.‎ 法二　因为∠ABC＝90°，所以可以以B为坐标原点，BC，BA分别为x，y轴，垂直于平面ABC的直线为z轴建立如图所示的空间直角坐标系B－xyz，‎ 则B(0，0，0)，A(0，1，0)，C(，0，0)，P(0，1，2)，‎ ＝(，0，0)，＝(0，1，2)，＝(0，0，2)，＝(，－1，0).‎ 设平面PAC的法向量n1＝(x，y，z)，‎ 由n1⊥，n1⊥，得取x＝1，则n1＝(1，，0).‎ 设平面PBC的法向量n2＝(x，y，z).‎ 由n2⊥，n2⊥，得 取z＝1，则n2＝(0，－2，1)，‎ 故|cos〈n1，n2〉|＝＝.‎ 所以二面角B－PC－A的余弦值为.‎ ‎21.(本小题满分15分)(2020·杭州二中模拟)如图，矩形ADFE和梯形ABCD所在平面互相垂直，AB∥CD，∠ABC＝∠ADB＝90°，CD＝1，BC＝2.‎ ‎(1)(一题多解)求证：BE∥平面DCF；‎ ‎(2)当AE的长为何值时，直线AD与平面BCE所成角的大小为45°.‎ ‎(1)证明　法一　如图，以D为坐标原点，‎ AD所在直线为x轴，BD所在直线为y轴，DF所在直线为z轴建立空间直角坐标系.‎ 设AE＝h，由CD＝1，BC＝2，∠ADB＝90°，‎ 依据三角形相似可得∠DCB＝90°，‎ 则DB＝，AB＝5，故由勾股定理可得AD＝2.‎ 所以D(0，0，0)，A(2，0，0)，B(0，，0)，‎ C，E(2，0，h)，F(0，0，h).‎ ＝，＝(0，0，h)，‎ ＝(2，－，h)，‎ 设平面DCF的法向量为n＝(x，y，z).‎ 所以化简得 令x＝，得n＝(，2，0)，·n＝0，‎ 故⊥n，又BE不在平面DCF上，‎ 所以BE∥平面DCF.‎ 法二　因为四边形ADFE是矩形，‎ 故AE∥DF.又AB∥CD，且AB∩AE＝A，CD∩DF＝D，AB，AE在平面ABE上，CD，DF在平面DCF上，‎ 故平面ABE∥平面DCF.‎ 又BE在平面ABE上，且BE不在平面CDF上，‎ 故BE∥平面CDF.‎ ‎(2)解　由(1)中法一可得＝(2，0，0)，‎ ＝，＝(2，－，h)，‎ 设平面BCE法向量为m＝(x1，y1，z1)，‎ 所以化简得 令y1＝h，得m＝(－2h，h，5).‎ 由题意得cos 45°＝＝＝，‎ 故h＝±，因为h＞0，所以AE＝h＝.‎ ‎22.(本小题满分15分)(2019·北京卷)如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA＝AD＝CD＝2，BC＝3.E为PD的中点，点F在PC上，且＝.‎ ‎(1)求证：CD⊥平面PAD.‎ ‎(2)求二面角F－AE－P的余弦值.‎ ‎(3)设点G在PB上，且＝.判断直线AG是否在平面AEF内，说明理由.‎ ‎(1)证明　因为PA⊥平面ABCD，CD⊂平面ABCD，所以PA⊥CD.‎ 又因为AD⊥CD，PA∩AD＝A，PA，AD⊂平面PAD，‎ 所以CD⊥平面PAD.‎ ‎(2)解　过点A作AD的垂线交BC于点M.‎ 因为PA⊥平面ABCD，AM，AD⊂平面ABCD，‎ 所以PA⊥AM，PA⊥AD.‎ 建立如图所示的空间直角坐标系A－xyz，则A(0，0，0)，B(2，－1，0)，C(2，2，0)，D(0，2，0)，P(0，0，2).‎ 因为E为PD的中点，所以E(0，1，1).‎ 所以＝(0，1，1)，＝(2，2，－2)，＝(0，0，2).‎ 所以＝＝，‎ 所以＝＋＝.‎ 设平面AEF的法向量为n＝(x，y，z)，则即 令z＝1，则y＝－1，x＝－1.‎ 于是n＝(－1，－1，1).‎ 又因为平面PAD的一个法向量为p＝(1，0，0)，‎ 所以cos〈n，p〉＝＝－.‎ 由题知，二面角F－AE－P为锐角，‎ 所以其余弦值为.‎ ‎(3)解　直线AG在平面AEF内.‎ 理由：因为点G在PB上，‎ 且＝，＝(2，－1，－2)，‎ 所以＝＝，‎ 所以＝＋＝.‎ 由(2)知，平面AEF的一个法向量n＝(－1，－1，1)，‎ 所以·n＝－＋＋＝0.‎ 又点A∈平面AEF，‎ 所以直线AG在平面AEF内.‎