2019-2020学年高中数学课时作业25正态分布的概念北师大版选修2-3 4页

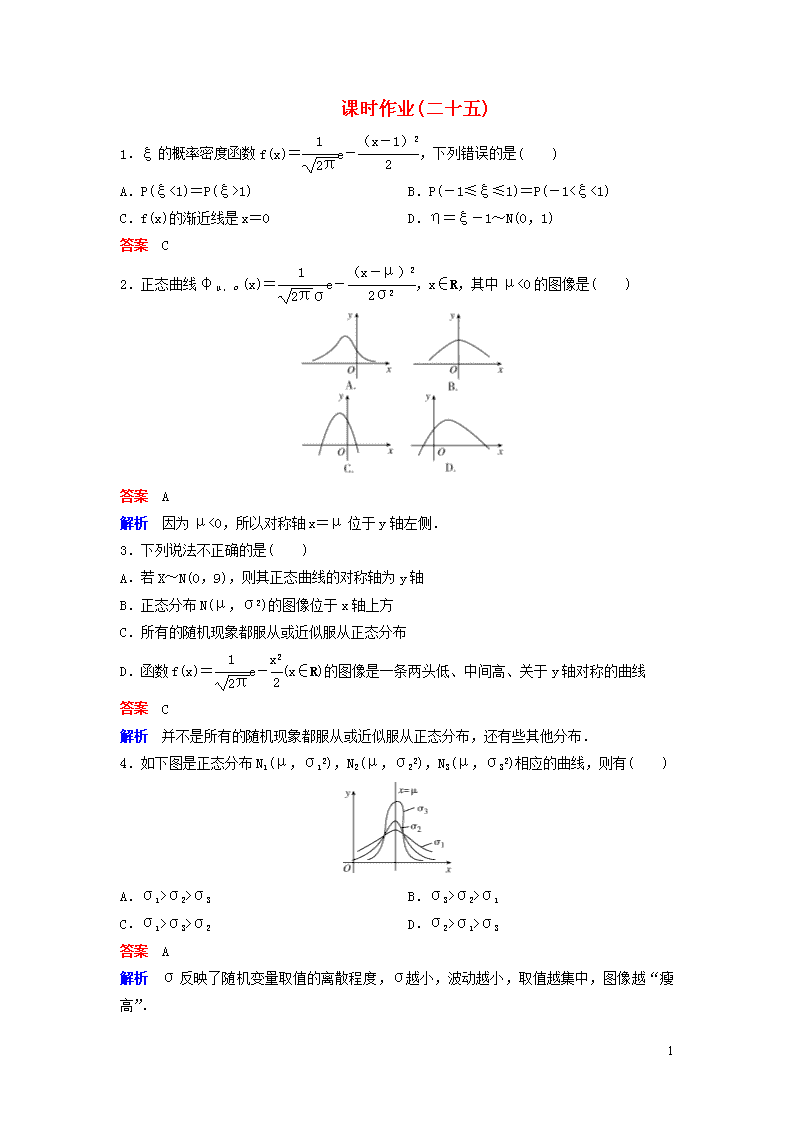
课时作业(二十五)‎ ‎1．ξ的概率密度函数f(x)＝e－，下列错误的是(　　)‎ A．P(ξ<1)＝P(ξ>1) B．P(－1≤ξ≤1)＝P(－1<ξ<1)‎ C．f(x)的渐近线是x＝0 D．η＝ξ－1～N(0，1)‎ 答案　C ‎2．正态曲线φμ，σ(x)＝e－，x∈R，其中μ<0的图像是(　　)‎ 答案　A 解析　因为μ<0，所以对称轴x＝μ位于y轴左侧．‎ ‎3．下列说法不正确的是(　　)‎ A．若X～N(0，9)，则其正态曲线的对称轴为y轴 B．正态分布N(μ，σ2)的图像位于x轴上方 C．所有的随机现象都服从或近似服从正态分布 D．函数f(x)＝e－(x∈R)的图像是一条两头低、中间高、关于y轴对称的曲线 答案　C 解析　并不是所有的随机现象都服从或近似服从正态分布，还有些其他分布．‎ ‎4．如下图是正态分布N1(μ，σ12)，N2(μ，σ22)，N3(μ，σ32)相应的曲线，则有(　　)‎ A．σ1>σ2>σ3　　　　　　　 B．σ3>σ2>σ1‎ C．σ1>σ3>σ2 D．σ2>σ1>σ3‎ 答案　A 解析　σ反映了随机变量取值的离散程度，σ越小，波动越小，取值越集中，图像越“瘦高”．‎ 4‎ ‎5．设随机变量ξ～N(2，4)，则D(ξ)的值等于(　　)‎ A．1 B．2‎ C. D．4‎ 答案　A 解析　∵ξ～N(2，4)，∴D(ξ)＝4.∴D(ξ)＝D(ξ)＝×4＝1.‎ ‎6．若随机变量ξ的密度函数为f(x)＝e－，ξ在(－2，－1)和(1，2)内取值的概率分别为P1，P2，则P1，P2的关系为(　　)‎ A．P1>P2 B．P1C)＝P，则P的值为(　　)‎ A．0 B．1‎ C. D．不确定与σ无关 答案　C 解析　∵P(ξ≤C)＝P(ξ>C)＝P，∴C＝μ，且P＝.‎ ‎8．已知随机变量ξ服从正态分布N(0，σ2)，若P(ξ>2)＝0.023，则P(－2≤ξ≤2)＝(　　)‎ A．0.477 B．0.628‎ C．0.954 D．0.977‎ 答案　C 解析　因为随机变量ξ服从正态分布N(0，σ2)，所以正态曲线关于直线x＝0对称，又P(ξ>2)＝0.023，所以P(ξ<－2)＝0.023，所以P(－2≤ξ≤2)＝1－P(ξ>2)－P(ξ<－2)＝1－2×0.023＝0.954，故选C.‎ ‎9．正态总体的函数f(x)＝e－(x∈R)，则总体的平均数E(X)＝________，标准差σ(X)＝________．‎ 答案　0　2‎ 解析　f(x)＝e－＝e－，对比正态曲线函数解析式可知μ＝0，σ＝2.‎ 4‎ ‎10．从正态分布曲线f(x)＝e，x∈R的图像可以看到曲线在________上方，关于________对称，当__________时，f(x)达到最大值，最大值是__________．‎ 答案　x轴　直线x＝8　x＝8　 解析　由正态分布曲线对应的有关特征可得．‎ ‎11．已知正态分布N(μ，σ2)的密度曲线是：‎ f(x)＝e－，x∈R.给出以下四个命题：‎ ‎①对任意x∈R，f(μ＋x)＝f(μ－x)成立；‎ ‎②如果随机变量X服从N(μ，σ2)，且F(x)＝P(X2)＝p，则P(0