2013年普通高等学校招生全国统一考试数学文试题（山东卷） 11页

‎2013年普通高等学校招生全国统一考试（山东卷）‎ 文科数学 参考公式：如果事件互斥，那么 一．选择题:本题共12个小题，每题5分，共60分。‎ ‎1．复数，则 ‎(A)25 (B) (C)5 (D) ‎ ‎2．已知集合均为全集的子集，且,,则 ‎(A){3} (B){4} (C){3,4} (D)‎ ‎3．已知函数为奇函数，且当时，，则 ‎(A)2 (B)1 (C)0 (D)-2‎ ‎4．一个四棱锥的侧棱长都相等，底面是正方形，其正（主）视图如右图所示该四棱锥侧面积和体积分别是 ‎(A) (B) (C) (D) 8,8‎ ‎5．函数的定义域为 ‎(A)(-3，0] (B) (-3，1] (C) (D) ‎ ‎6．执行右边的程序框图，若第一次输入的的值为-1.2，第二次输入的的值为1.2，则第一次、第二次输出的的值分别为 ‎(A)0.2，0.2 (B) 0.2，0.8 (C) 0.8，0.2 (D) 0.8，0.8‎ ‎7．的内角的对边分别是，‎ 若，，，则 ‎(A) (B) 2 (C) (D)1‎ ‎8．给定两个命题，的必要而不充分条件，则 ‎(A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件 ‎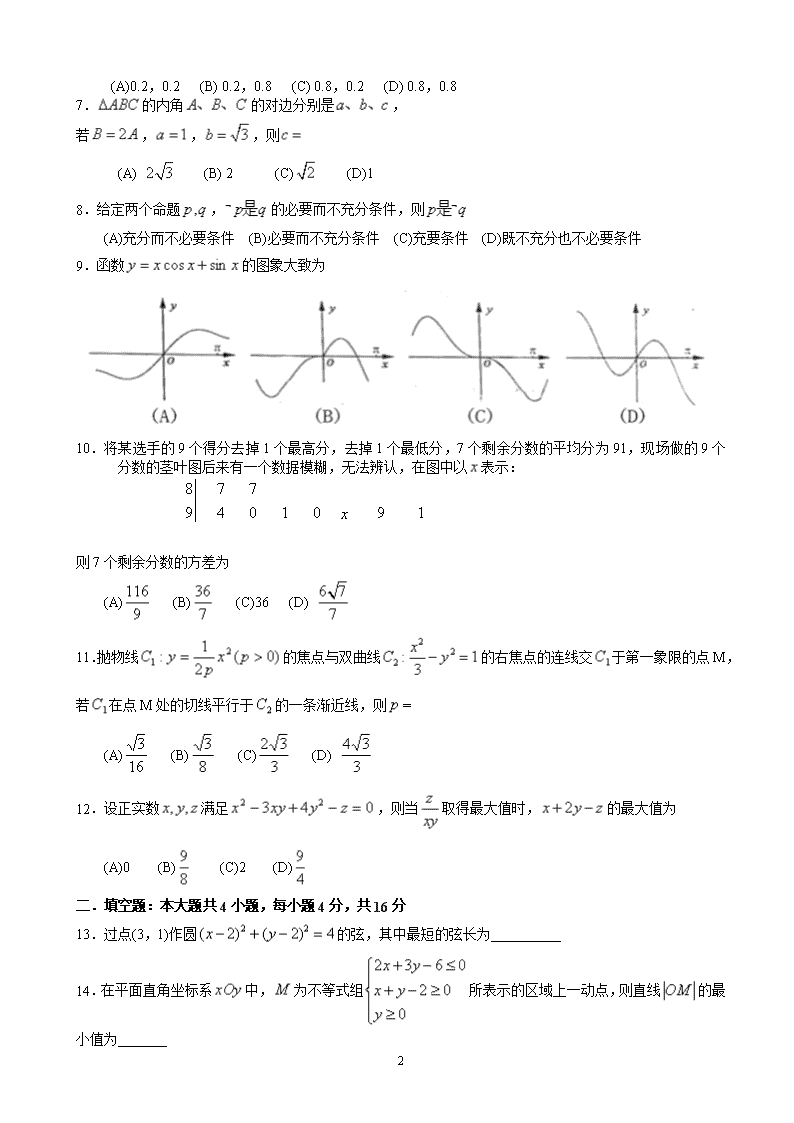9．函数的图象大致为 ‎10．将某选手的9个得分去掉1个最高分，去掉1个最低分，7个剩余分数的平均分为91，现场做的9个分数的茎叶图后来有一个数据模糊，无法辨认，在图中以表示：‎ ‎ ‎‎8 7 7‎ ‎9 4 0 1 0 9 1‎ x 则7个剩余分数的方差为 ‎(A) (B) (C)36 (D) ‎ ‎11．抛物线的焦点与双曲线的右焦点的连线交于第一象限的点M，若在点M处的切线平行于的一条渐近线，则=‎ ‎(A) (B) (C) (D) ‎ ‎12．设正实数满足，则当取得最大值时，的最大值为 ‎(A)0 (B) (C)2 (D)‎ 二．填空题：本大题共4小题，每小题4分，共16分 ‎13．过点(3，1)作圆的弦，其中最短的弦长为__________‎ ‎14．在平面直角坐标系中，为不等式组所表示的区域上一动点，则直线的最小值为_______‎ ‎15．在平面直角坐标系中，已知，，若，则实数的值为______‎ ‎16．定义“正对数”：，现有四个命题：‎ ‎①若，则；‎ ‎②若，则 ‎③若，则 ‎④若，则 ‎ 其中的真命题有____________(写出所有真命题的序号)‎ 三．解答题：本大题共6小题，共74分，‎ ‎17．(本小题满分12分)‎ ‎ 某小组共有五位同学，他们的身高（单位:米）以及体重指标（单位:千克/米2）‎ 如下表所示：‎ A B C D E 身高 ‎1.69‎ ‎1.73‎ ‎1.75‎ ‎1.79‎ ‎1.82‎ 体重指标 ‎19.2‎ ‎25.1‎ ‎18.5‎ ‎23.3‎ ‎20.9‎ ‎(Ⅰ)从该小组身高低于1.80的同学中任选2人，求选到的2人身高都在1.78以下的概率 ‎(Ⅱ)从该小组同学中任选2人，求选到的2人的身高都在1.70以上且体重指标都在[18.5，23.9)中的概率 ‎18．(本小题满分12分)‎ 设函数，且的图象的一个对称中心到最近的对称轴的距离为，‎ ‎ (Ⅰ)求的值 ‎(Ⅱ)求在区间上的最大值和最小值 ‎19．(本小题满分12分)‎ 如图，四棱锥中，,,分别为 的中点 ‎(Ⅰ)求证：；(Ⅱ)求证：‎ ‎20．(本小题满分12分)‎ 设等差数列的前项和为，且,‎ ‎(Ⅰ)求数列的通项公式 ‎(Ⅱ)设数列满足 ，求的前项和 ‎21．(本小题满分12分)‎ ‎ 已知函数 ‎(Ⅰ)设，求的单调区间 ‎ (Ⅱ) 设，且对于任意，。试比较与的大小 ‎22．(本小题满分14分)‎ 在平面直角坐标系中，已知椭圆C的中心在原点O，焦点在轴上，短轴长为2，离心率为 ‎(I)求椭圆C的方程 ‎ (II)A,B为椭圆C上满足的面积为的任意两点，E为线段AB的中点，射线OE交椭圆C与点P，设，求实数的值。‎ 参考答案 一、选择题 ‎1．C ‎2．A ‎3．D ‎4．B ‎5．A ‎6．C ‎7．B ‎8．A ‎9．D ‎10．B ‎11．D ‎12．C ‎13． ‎ ‎14． ‎ ‎15．5 ‎ ‎16．①③④ ‎ ‎17．‎ ‎18．‎ ‎19．‎ ‎20．‎ ‎21．‎ 当时函数的单调递减区间是 ‎22．‎ 将代入椭圆方程，得 ‎ ‎