河南省顶级名校2020-2021学年高二上学期开学测试数学试卷 11页

数学试题 说明：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）．全卷满分 150 分．考 试时间 120 分钟．‎ ‎2．将第Ⅰ卷的答案代表字母填(涂)在第Ⅱ卷的答案题表(答题卡)中．全部答 案在答题卷上完成，答在试题卷上无效．‎ 第Ⅰ卷   （选择题   共 60 分）‎ 一．选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一 项是符合题目要求的．‎ ‎1．设全集 U  = R ，集合 M  = {x | y = 3 - 2x} ， N  = {y | y = 3 - 2x} ，则图中阴影部 A.{x |‎ <  x £ 3} B.{x |‎ <  x < 3}‎ C.{x |‎ £  x < 3} D.{x |‎ <  x < 2}‎ ‎2． sin 34   sin 26   - cos 34   cos 26   的值是 A． 1‎ ‎2 B． 3‎ ‎2 C． - ‎3．在∆ABC 中，角 A、B、C 的对边分别为 a、b、c，若 p p p ‎6‎ ‎4‎ ‎3‎ ‎5p ‎12‎ 分表示的是( )‎ ‎3              3‎ ‎2 2‎ ‎3              3‎ ‎2 2‎ ‎0 0 0 0‎ A. B. C.‎ ‎‎ ‎1‎ ‎2‎ ‎‎ M D． - D.‎ ‎‎ ‎3‎ ‎2‎ ‎‎ N ‎‎ U ‎‎ ‎，则角 A ‎4.有下列命题：‎ ‎①若直线 l 平行于平面α内的无数条直线，则直线 l∥α；‎ ‎②若直线 a 在平面α外，则 a∥α；‎ ‎③若直线 a∥b，b∥α，则 a∥α；‎ ‎④若直线 a∥b，b∥α，则 a 平行于平面α内的无数条直线．‎ 其中真命题的个数是( )‎ A．1 B．2 C．3 D．4‎ ‎5．直线 4x - 3 y + 6 = 0 与圆 ( x - 4)   + ( y + 1) = 25 的位置关系是（‎ ‎2 2‎ ‎）‎ ‎6．函数 y 3 cos x 3 5 图象的一个对称中心和一条对称轴可以是（‎ A．相离 B．相交但不过圆心 C．相交且过圆心 D．相切 ‎‎ 高二入学测试   数学试题卷    第 1页   共  6页 ‎‎ ‎）‎ A. 5   ，0   ，x 3 B. 5   ，5   ，x 3‎ ‎ v   v v D.C. 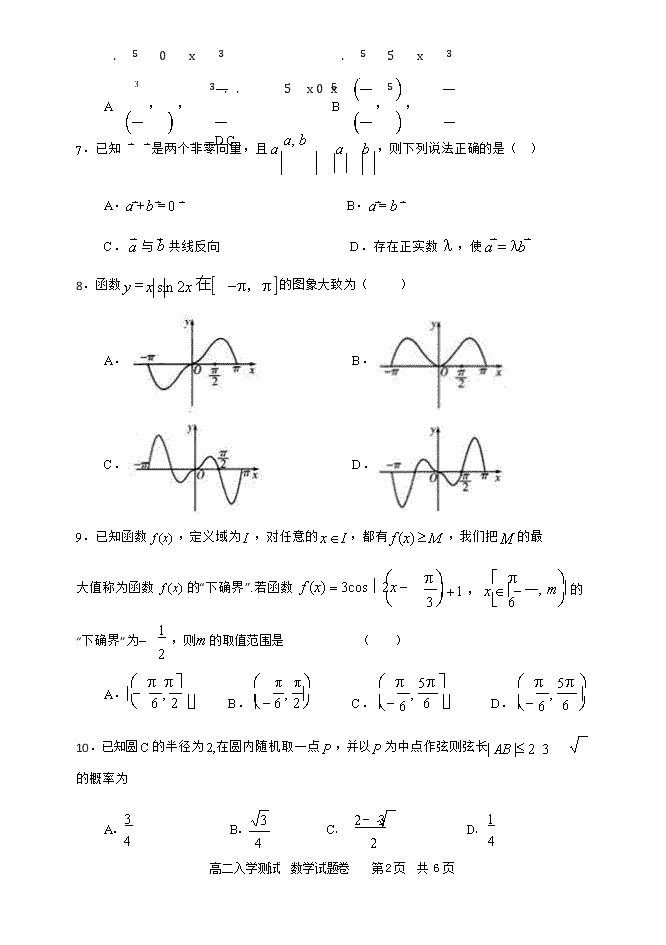a, b   0 x 5 v + b   =   v  + 3v 5 x 5‎ ‎7．已知 3 是两个非零向量，且 a a b  ，则下列说法正确的是（   ）‎ v v v v v A． a + b = 0‎ ‎‎ B． a = b C． a 与 b 共线反向 D．存在正实数 l ，使 a = lb v v v v -p，p ‎8．函数 y = x sin 2x在[ ] 的图象大致为（ ）‎ A． B．‎ C． D．‎ ‎9．已知函数  f (x) ，定义域为 I  ，对任意的 x Î I ，都有 f (x) ³ M  ，我们把 M  的最 大值称为函数  f (x) 的“下确界”.若函数  f (x) = 3cos ç 2x - ÷ +1 ， x Î ê- ‎, m ÷ 的 æ è ‎‎ p ö               é   p ‎3 ø               ë   6‎ ‎‎ ö ø ‎“下确界”为 - ‎1‎ ‎2‎ ‎‎ ‎，则 m 的取值范围是                      （       ）‎ æ   p  p ù æ p   p ö æ   p 5p ù æ   p 5p  ö è 6 2 ø C． ç - ‎6  úû D． ç - è 6 2 úû B． ç - è 6‎ è 6‎ ‎6   ø A． ç - , ,   ÷ , , ÷ ‎10．已知圆 C 的半径为 2,在圆内随机取一点 P ，并以 P 为中点作弦则弦长 | AB |£ 2  3‎ 的概率为 A.‎ ‎‎ ‎3‎ ‎4‎ ‎‎ B.‎ ‎‎ ‎3‎ ‎4‎ ‎‎ C.‎ ‎‎ ‎2 -   3‎ ‎2‎ ‎‎ D.‎ ‎‎ ‎1‎ ‎4‎ 高二入学测试   数学试题卷 第 2页   共  6页 则当 x > 3 时， x   + y   的取值范围是（ ）‎ ‎11．已知函数 y = f (x) 是定义在 R 上的增函数，函数 y = f (x -1) 的图象关于点 ‎(1, 0) 对称，若任意的 x, y Î R ，不等式 f (x2 - 6x + 21) + f ( y2 - 8 y) < 0 恒成立，‎ ‎2 2‎ A． (3, 7) B． (9, 25) C． (13, 49) D． (9, 49)‎ ‎12．已知 OA  = 1 ， OB  =uuur uuur ‎uuur  uuur ‎3 ，OA ×OB = 0 ，点 C 在线段 AB 上，且 ÐAOC = 30o ，‎ 设 OC  =  mOA + nOB   (m, n Î R) ，则 m uuur uuur uuur ‎‎ n   等于 ‎‎ ‎（     ）‎ ‎3 B.  3‎ ‎3 D. 3‎ A． 1‎ ‎C．     3‎ 第Ⅱ卷   （非选择题   共 90 分）‎ 二．填空题：本大题共 4 小题，每小题 5 分．‎ ‎13.已知函数  f (x) = í ì  2-2 , x £ -1,‎ î3x + 3, x > -1,‎ ‎‎ 则满足 f (a) £ 4 的实数 a 的取值范围是 ‎________．‎ ‎14.100 个个体分成 10 组，编号后分别为第 1 组：00，01，02，…，09；第 2 组：10，‎ ‎11，12，…，19；…；第 10 组：90，91，92，…，99．现在从第 k 组中抽取其号码 的个位数与 ( k + m -1) 的个位数相同的个体，其中 m 是第 1 组随机抽取的号码的个 位数，则当 m = 5 时，从第 7 组中抽取的号码是 ．‎ ‎, ,L, ,L 的前 n 项和 Sn  = ‎15.数列 ,‎ ‎1 1 1 1‎ ‎2   2 + 3   2 + 3 + 4 2 + 3 + 4 + L+ ( k +1 ) ‎‎ ‎.‎ ‎16．给出下列命题：①当函数 y = 2 cosa - 3sina 取得最大值时， tan a  = - ‎3‎ ‎；‎ ‎2‎ ‎②设集合 A＝{0,1,2}，B＝{0,1,2}，分别从集合 A 和 B 中随机取一个数 a 和 b，‎ 确定平面上一个点 P(a，b)，设“点 P(a，b)落在直线 x＋y＝n 上”为事件 Cn(0≤n≤4，n∈N)，‎ 若事件 Cn 的概率最大，则 n 的可能值为 4 ；‎ £ x < 2kp+ ,k ÎZ}‎ ‎③函数 f (x) = lg(tan x -1) +   cos x 的定义域是{x | 2kp+ ‎p                 p ‎4                 2‎ 高二入学测试   数学试题卷 第 3页   共  6页 ‎④已知点 P 为 DABC 内一点， PA + 2PB + 3PC = 0 ，则 DAPB, DAPC, DBPC uuuv uuuv uuuv r 的面积之比为 3: 2 :1 ．其中说法正确的序号是 ．‎ 三．解答题：本大题共 6 小题．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本小题满分 10 分）‎ 在△ABC 中，已知角 A，B，C  所对的边分别为  a，b，c，且 a cos B - b cos A = b + c .‎ ‎(1)求角 A 的大小；‎ ‎(2)若 a = 4 ，D 是 BC 的中点，且 AD = ‎‎ ‎2 3‎ ‎3‎ ‎‎ ‎，求△ABC 的面积.‎ ‎18.  四棱锥 P - ABCD 的底面 ABCD 为直角梯形， AB ∥ CD ， AB ^ AD ，‎ AB = ‎1‎ ‎2‎ ‎‎ CD = 1， PA ^ 平面 ABCD ， PA = AD =   3 .‎ ‎（1）求证： PD ^ AB ；‎ ‎（2）求四棱锥 P - ABCD 的体积.‎ 高二入学测试   数学试题卷 第 4页   共  6页 ‎19.（本小题满分 12 分）‎ 已知函数  f ( x) = sin ç 2x + ÷ , g ( x ) =  A sin (wx + j ) ç A > 0，w > 0，j  < ‎2 ø æ è ‎‎ p ö                                    æ ‎6 ø                                    è ‎‎ p ö ÷ 的 ë 4 6 úû， ,不等式   f ( x) - m  < 2 恒成立,求实数 m 的取值范围.‎ ‎(2)若对于任意的 x Î ê- 部分图象如图所示.‎ ‎(1)求 g ( x) 的解析式,并说明 f ( x ) 的图象怎样经过 2 次变换得到 g ( x) 的图象；‎ é   p   p ù ‎20．（本小题满分 12 分）‎ 已 知 DABC  中 ， 顶 点 A(2, 2) ， 边 AB  上 的 中 线 CD  所 在 直 线 的 方 程 是 x + y = 0 ，边 AC 上高 BE 所在直线的方程是 x + 3y + 4 = 0 ．‎ ‎（1）求点 B 、 C 的坐标；‎ ‎（2）求 DABC 的外接圆的方程．‎ 高二入学测试   数学试题卷 第 5页   共  6页 ‎21．（本小题满分 12 分）‎ 已知关于 x 的二次函数 f(x)＝ax2－bx＋1(a≠0)，分别从集合 P 和 Q 中随机取一个数 a 和 b 得到的数对(a，b)．‎ ‎(1)若 a Î P = {1,2,3} ，b Î Q = {-1,1,2,3,4,} ，列举出所有的数对(a，b)，并求函 数 y＝f(x)有零点的概率；‎ ‎(2)若 a Î P = {x |1 £ x £ 3} ， b Î Q = {x | -1 £ x £ 4}，求函数 y＝f(x)在区间 ‎[1，＋∞)上是增函数的概率．‎ ‎22．（本小题满分 12 分）‎ 已知向量   a = ( 2, 2 cos 2(wx + j)),b = (‎ ‎, - r r ‎‎ ‎2        2‎ ‎2        2‎ ‎‎ ‎) ，其中 w > 0, 0 < j < ‎‎ p ‎2‎ ‎‎ ‎．‎ 函数 f ( x) = a × b 的图象过点 B (1, 2) ，点 B 与其相邻的最高点的距离为 4 ．‎ r  r ‎（1）求函数 f ( x ) 的单调递减区间；‎ ‎（2）计算 f (1) + f (2) + f (3) +KK + f (2021) ；‎ ‎（3）设函数 g ( x ) = f ( x ) - m - 1 ，试讨论函数 g ( x ) 在区间[0,3]上的零点个数．‎ 高二入学测试   数学试题卷 第 6页   共  6页 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5            6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C C A D           B D C A A C B 数学参考答案 第Ⅰ卷   （选择题，共 60 分）‎ 一．选择题：本大题共 12 小题，每小题 5 分．‎ 第Ⅱ卷   （  非选择题，共 90 分）‎ 二．填空题：本大题共 4 小题，每小题 5 分．‎ ‎(-¥, ]‎ ‎13．‎ ‎1‎ ‎3‎ ‎14．              61‎ ‎15． 11 2  æ 1‎ ‎1 1 ö ç ÷ ‎9 3  è n + 1 n + 2 n + 3 ø ‎‎ -                     +          + ‎‎ ‎16.               ①④‎ 三．解答题：本大题共 6 小题.  解答应写出文字说明，证明过程或演算步骤 ‎17．（1） A = ‎‎ ‎2p ‎3‎ ‎‎ ‎（2）‎ ‎‎ ‎4 3‎ ‎3‎ ‎18．解：（1）因为 PA ^ 平面 ABCD ， AB Ì 平面 ABCD ，‎ 所以 PA ^ AB ，‎ 又因为 AB ^ AD ， AB I PA = A 所以 AB ^ 平面 PAD .‎ 又 PD Ì 平面 PAD ，所以 AB ^ PD .………………………………6 分 ( AB + CD ) × AD = ‎（2） S梯形ABCD = ‎‎ ‎1                              3  3‎ ‎2                                 2‎ ‎‎ ‎，‎ 又 PA ^ 平面 ABCD ，‎ 所以V四棱锥P-ABCD = ‎1‎ ‎3‎ ‎‎ ´ S梯形ABCD × PA ‎1 3 3 3 .………………………………12 分 ‎3 2‎ ‎2‎ =   ´ ´   3 = ‎19.解：(1)由图得 A = 1，w = ‎‎ ‎1‎ ‎2‎ ‎‎ ‎,‎ 高二入学测试   数学试题卷 第 1页   共  5页 æ 2p ö è ø，÷ 为函数递增区间上的零点,‎ ‎3‎ 所以 - × + j = 2kp，k Î Z ,即j  = 2kp  + ，k Î Z  .‎ 因为 ç - 0‎ ‎2p   1 p ‎3 2 3‎ ‎,即 g ( x ) = sin ç ‎3 ø 因为 j  < ‎p ‎2‎ ‎‎ ‎,所以 j = ‎p ‎3‎ ‎æ 1‎ è 2‎ ‎‎ x + ‎p ö ÷ ，‎ 将函数 f ( x ) 的图象上所有点的横坐标伸长到原来的 4 倍(纵坐标不变),再将所得图象 p  个单位长度可得 g ( x) ；………………………………6 分 向左平移 ‎‎ ‎3‎ ë 4 6 û，  ú ,所以 2x + ‎(2)因为 x Î ê- Πê- ，  ú ,‎ é   p   p ù ‎p ‎6‎ ‎é   p   p ù ë   3   2 û =- 时,  f ( x ) 取最小值 - = 时,  f ( x ) 取最大值 1,‎ 所以当 2x + ‎p       p ‎6        3‎ ‎3‎ ‎2‎ ‎‎ ‎,当 2x + ‎p     p ‎6     2‎ 因为  f ( x) - m < 2 恒成立,即 -2 + m < f ( x) < 2 + m 恒成立,‎ ï-2 + m < - m Î çç -1，- ‎3 ö ‎2   ÷ø 所以 ‎‎ ì í î ï1 < 2 + m ‎‎ ‎3‎ ‎2‎ ‎‎ ‎,即 ‎‎ æ è ‎‎ ‎2‎ ‎‎ ÷ ‎‎ ‎.………………………………12 分 ‎20.  解：（1）由题意可设 B(-3a - 4, a) ，则 AB 的中点 D ( , ) 必在直线 -3a - 2  a + 2‎ ‎2 2‎ CD 上，‎ + = 0 ，∴ a = 0 ，∴ B(-4, 0) ，‎ ‎∴‎ ‎-3a - 2‎ ‎2‎ ‎a + 2‎ ‎2‎ 又直线AC方程为： y - 2 = 3(x - 2) ，即 y = 3x - 4 ，‎ î y = 3x - 4‎ 由 ‎‎ ìx + y = 0‎ í ‎‎ 得， C(1, -1) ………………………………6 分 ‎（2）设△ABC外接圆的方程为 x   + y + Dx + Ey + F  =  0 ，‎ ‎2 2‎ 高二入学测试   数学试题卷 第 2页   共  5页 ì2   + 2   + 2D + 2E + F  = 0‎ 则 í(-4)   - 4D + F  = 0‎ ï1+1+ D - E + F  = 0‎ ïD =  4‎ ‎11‎ 得 íE = - ‎4‎ î ï 2‎ î ‎‎ ‎2      2‎ ‎‎ ì       9‎ ï ï ï ïF = -7‎ ï x - ‎∴△ABC 外接圆的方程为 ‎‎ x2 + y2 + ‎‎ ‎9      11‎ ‎4       4‎ ‎‎ y - 7 = 0‎ ‎‎ ‎．………………………12 分 ‎21.解：(1)(a，b)共有(1，－1)，(1,1)，(1,2)，(1,3)，(1,4)，(2，－1)，(2,1)，(2,2)，(2,3)，‎ ‎(2,4)，(3，－1)，(3,1)，(3,2)，(3,3)，(3,4)，15 种情况．‎ 设函数 y＝f(x)有零点的事件为 A 函数 y＝f(x)有零点，Δ＝b2－4a≥0，‎ 其基本事件有(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)共 6 种情况 ‎15  ＝  .………………………………6 分 所以函数 y＝f(x)有零点的概率为 P( A) = ‎6         2‎ ‎‎ ‎5‎ ‎2a，‎ ‎2a≤1，即 b－2a≤0.‎ 因此 W = {(a, b) | íì1 £ a £ 3‎ ‎}， B = {(a, b) | í-1 £ b £ 4}‎ ïb £ 2a ‎(2)函数 y＝f(x)的对称轴为 x＝ b 设 f (x) 在区间[1，＋∞)上是增函数的事件为 B ，则有 b ì1 £ a £ 3‎ ï î-1 £ b £ 4‎ î 作出图形（略），由图知：所以函数 y＝f(x)在区间[1，＋∞)上是增函数的概率为 P(B) = B   = ‎2 ´ 5 - × 2 ´1‎ S SW ‎1‎ ‎2‎ ‎2 ´ 5‎ ‎‎ = ‎‎ ‎9‎ ‎10‎ ‎‎ ‎.‎ 故事件 A 的概率为 ‎2‎ ‎5‎ ‎‎ ‎；事件 B 的概率为 ‎9‎ ‎10‎ ‎‎ ‎.……………………12 分 ‎22.解：  (1)Q向量 a = ( 2, 2 cos 2(wx + j)),b = (‎ ‎, - r r ‎2        2‎ ‎2        2‎ ‎‎ ‎)  ，‎ 高二入学测试   数学试题卷 第 3页   共  5页 f (x) = 1 - cos 2(wx + j) ，‎  f ( x )max = 2, 点 B (1, 2) 为函数 f ( x ) 图象上的一个最高点，‎ = 4,w = ，‎ Q点 B 与其相邻的最高点的距离为 4 ， ‎2p                  p ‎2w                  4‎ Q函数  f ( x ) 图象过点 B (1, 2) ，1- cos ç + 2j ÷ = 2,sin 2j = 1 ，‎ æ p è 2‎ ‎ö ø ‎,j  = ‎， f ( x ) = 1- cos 2 ç ÷ = 1+ sin Q 0 < j < ‎‎ p            p ‎2            4‎ ‎‎ æ p è 4‎ ‎‎ x + ‎‎ p ö ‎4 ø ‎‎ p ‎2‎ ‎‎ x ，‎ 由 2kp + £ x £ 2kp + ，得 4k +1£ x £ 4k + 3， k Î Z  ．‎ p p ‎2 2‎ ‎3p ‎2‎ ‎∴ f (x) 的单调递减区间是[4k +1,4k + 3] ， k Î Z ．………………………4 分 ‎(2)  由（1）知 f ( x ) = 1+ sin ‎p ‎2‎ ‎‎ x, f (x ) 的周期为 4，且 ‎(3) g ( x ) =  f ( x ) - m - 1 = sin x - m ，函数 g ( x ) 在区间[0,3]上的零点个数，即为 函数 y = sin x 的图象与直线 y = m 在[0,3]上的交点个数．‎ 由图象可知（图略），①当 m > 1或 m < -1 时，函数 y = sin x 的图象与直线 y = m x 的图象与直线 y = m 在[0,3]上有一个公共点，即函数 g ( x ) 有一个零点；‎ y = sin ‎③当 0 £ m < 1 时，函数 y = sin x 的图象与直线 y = m 在[0,3]上有两个公共点，即 f (1) = 2, f (2 ) = 1, f (3 ) = 0, f (4 ) = 1 ， f (1) + f (2) + f (3) + f (4 ) = 4 ，‎ 而 2021 = 4 ´ 505 +1‎ ‎∴ f (1) + f (2) + f (3) +KK + f (2021) = 4 ´ 505 + 2 = 2022 ．‎ ‎………………………………8 分 p ‎2‎ p ‎2‎ p ‎2‎ 在 [0,3] 上的无公共点，即函数 g ( x ) 无零点；②当 -1 £ m < 0 与 m = 1时，函数 p ‎2‎ p ‎2‎ 高二入学测试   数学试题卷 第 4页   共  5页 函数 g ( x ) 有两个零点．‎ 综上：当 m Î (-¥,-1) U (1,+¥) 时， g(x) 的零点个数为 0 ；‎ 当 m Î[-1,0) U{1} 时， g(x) 的零点个数为1；‎ 当 m Î[0,1) 时， g(x) 的零点个数为 2 ．……………………12 分 高二入学测试   数学试题卷 第 5页   共  5页