2005年上海市高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】 5页

‎2005年上海市高考数学试卷（理科）‎ 一、填空题（共12小题，每小题4分，满分48分）‎ ‎1. 函数f(x)=log‎4‎(x+1)‎的反函数f‎-1‎‎(x)=‎________．‎ ‎2. 方程‎4‎x‎+‎2‎x-2=0‎的解是________．‎ ‎3. 直角坐标平面xOy中，若定点A(1, 2)‎与动点P(x, y)‎满足OP‎→‎‎⋅OA‎→‎=4‎，则点P的轨迹方程是________．‎ ‎4. 在‎(x-a‎)‎‎10‎的展开式中，x‎7‎的系数是‎15‎，则实数a=‎________．‎ ‎5. 若双曲线的渐近线方程为y=±3x，它的一个焦点是‎(‎10‎，0)‎，则双曲线的方程是________．‎ ‎6. 将参数方程x=1+2cosθ,‎y=2sinθ,‎‎ ‎（θ为参数）化成普通方程为________．‎ ‎7. 计算：limn→∞‎‎3‎n‎+1‎‎3‎n+1‎‎+‎‎2‎n‎=‎________．‎ ‎8. 某班有‎50‎名学生，其中‎15‎人选修A课程，另外‎35‎人选修B课程，从班级中任选两名学生，他们是选修不同课程的学生的概率是________．（结果用分数表示）‎ ‎9. 在‎△ABC中，若‎∠A=‎‎120‎‎∘‎，AB=5‎，BC=7‎，则‎△ABC的面积S=‎________．‎ ‎10. 函数f(x)‎＝sinx+2|sinx|‎，x∈[0, 2π]‎的图象与直线y＝k有且仅有两个不同的交点，则实数k的取值范围是________．‎ ‎11. 有两个相同的直三棱柱，高为‎2‎a，底面三角形的三边长分别为‎3a，‎4a，‎5a(a>0)‎，用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，全面积最小的是一个四棱柱，则a的取值范围是________．‎ ‎12. 用n个不同的实数a‎1‎，a‎2‎，…，an可得到n!个不同的排列，每个排列为一行写成一个n!行的数阵．对第i行ai1‎，ai2‎，…，ain，记bi‎=-ai1‎+2ai2‎-3ai3‎+...+(-1‎)‎nnain(i=1, 2, 3‎,…,n!‎)‎．例如：用‎1‎，‎2‎，‎3‎可得数阵如下，由于此数阵中每一列各数之和都是‎12‎，所以，b‎1‎‎+b‎2‎+...+b‎6‎=-12+2×12-3×12=-24‎．那么，在用‎1‎，‎2‎，‎3‎，‎4‎，‎5‎形成的数阵中，b‎1‎‎+b‎2‎+...+b‎120‎=‎________．‎ 二、选择题（共4小题，每小题4分，满分16分）‎ ‎13. 若函数f(x)=‎‎1‎‎2‎x‎+1‎，则该函数在‎(-∞, +∞)‎上是（ ）‎ A.单调递减无最小值 B.单调递减有最小值 C.单调递增无最大值 D.单调递增有最大值 ‎14. 已知集合M={x||x-1|≤2,x∈R}，P={x|‎5‎x+1‎≥1，x∈Z}‎，则M∩P等于（ ）‎ A.‎{x|00‎ B.b>0‎且c<0‎ C.b<0‎且c＝‎0‎ D.b≥0‎且c＝‎‎0‎ 三、解答题（共6小题，满分86分）‎ ‎17. 已知直四棱柱ABCD-‎A‎1‎B‎1‎C‎1‎D‎1‎中，AA‎1‎=2‎，底面ABCD是直角梯形，‎∠A=‎‎90‎‎∘‎，AB // CD，AB=4‎，AD=2‎，DC=1‎，求异面直线BC‎1‎与DC所成的角的大小．（结果用反三角函数表示）‎ ‎ 5 / 5‎ ‎18. 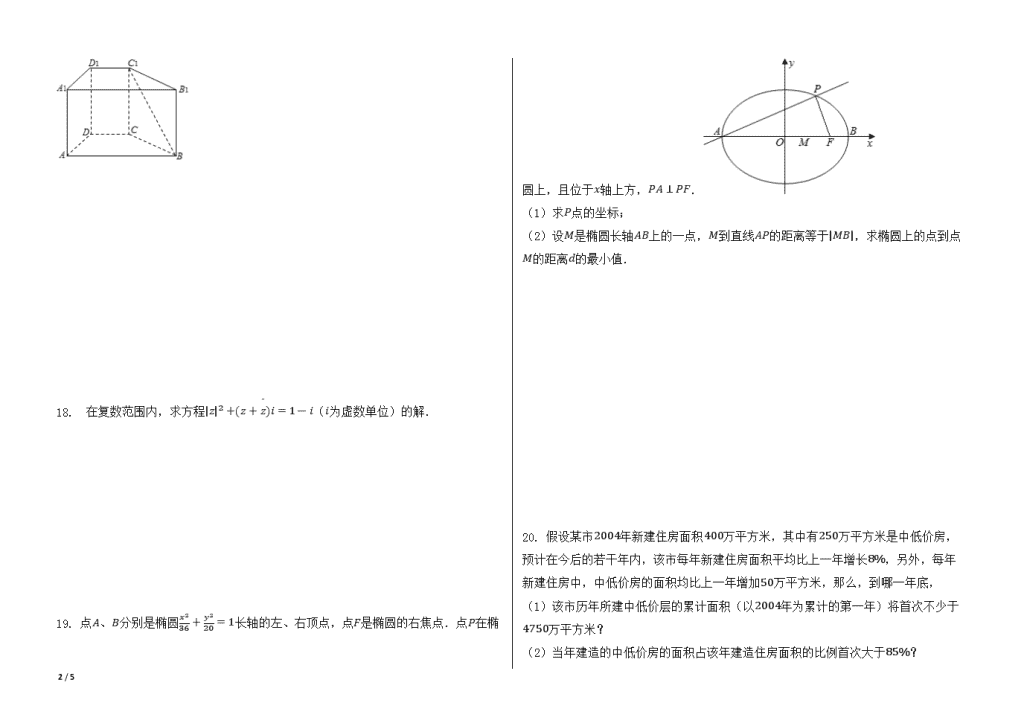在复数范围内，求方程‎|z‎|‎‎2‎+(z+z‎¯‎)i=1-i（i为虚数单位）的解．‎ ‎19. 点A、B分别是椭圆x‎2‎‎36‎‎+y‎2‎‎20‎=1‎长轴的左、右顶点，点F是椭圆的右焦点．点P在椭圆上，且位于x轴上方，PA⊥PF．‎ ‎（1）求P点的坐标；‎ ‎（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于‎|MB|‎，求椭圆上的点到点M的距离d的最小值．‎ ‎20. 假设某市‎2004‎年新建住房面积‎400‎万平方米，其中有‎250‎万平方米是中低价房，预计在今后的若干年内，该市每年新建住房面积平均比上一年增长‎8%‎，另外，每年新建住房中，中低价房的面积均比上一年增加‎50‎万平方米，那么，到哪一年底，‎ ‎（1）该市历年所建中低价层的累计面积（以‎2004‎年为累计的第一年）将首次不少于‎4750‎万平方米？‎ ‎（2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于‎85%‎？‎ ‎ 5 / 5‎ ‎21. 对定义域是Df．Dg的函数y＝f(x)‎．y＝g(x)‎，‎ 规定：函数h(x)=f(x)g(x),x‎∈Dfx‎∈Dgf(x),x‎∈Dfx‎∉Dgg(x),x‎∉Dfx‎∈Dg ‎．‎ ‎（1）若函数f(x)=‎‎1‎x-1‎，g(x)‎＝x‎2‎，写出函数h(x)‎的解析式；‎ ‎（2）求问题（1）中函数h(x)‎的值域；‎ ‎（3）若g(x)‎＝f(x+α)‎，其中α是常数，且α∈[0, π]‎，请设计一个定义域为R的函数y＝f(x)‎，及一个α的值，使得h(x)‎＝cos4x，并予以证明．‎ ‎22. 在直角坐标平面中，已知点P‎1‎‎(1, 2)‎，P‎2‎‎(2, ‎2‎‎2‎)‎，P‎3‎‎(3, ‎2‎‎3‎)‎，…，Pn‎(n, ‎2‎n)‎，其中n是正整数．对平面上任一点A‎0‎，记A‎1‎为A‎0‎关于点P‎1‎的对称点，A‎2‎为A‎1‎关于点P‎2‎的对称点，…，An为An-1‎关于点Pn的对称点．‎ ‎（1）求向量A‎0‎A‎2‎‎→‎的坐标；‎ ‎（2）当点A‎0‎在曲线C上移动时，点A‎2‎的轨迹是函数y=f(x)‎的图象，其中f(x)‎是以‎3‎位周期的周期函数，且当x∈(0, 3]‎时，f(x)=lgx．求以曲线C为图象的函数在‎(1, 4]‎上的解析式；‎ ‎（3）对任意偶数n，用n表示向量A‎0‎An‎→‎的坐标．‎ ‎ 5 / 5‎ 参考答案与试题解析 ‎2005年上海市高考数学试卷（理科）‎ 一、填空题（共12小题，每小题4分，满分48分）‎ ‎1.‎‎4‎x‎-1‎ ‎2.‎‎0‎ ‎3.x+2y-4‎＝‎‎0‎ ‎4.‎‎-‎‎1‎‎2‎ ‎5.‎x‎2‎‎-y‎2‎‎9‎=1‎ ‎6.‎‎(x-1‎)‎‎2‎+y‎2‎=4‎ ‎7.‎‎1‎‎3‎ ‎8.‎‎3‎‎7‎ ‎9.‎‎15‎‎3‎‎4‎ ‎10.‎‎(1, 3)‎ ‎11.‎‎00‎，只能x=‎‎3‎‎2‎，于是y=‎‎5‎‎3‎‎2‎．∴ 点P的坐标是‎(‎3‎‎2‎, ‎5‎‎3‎‎2‎)‎．‎ ‎（2）直线AP的方程是 y-0‎‎5‎‎3‎‎2‎‎-0‎‎=‎x+6‎‎3‎‎2‎‎+6‎，即 x-‎3‎y+6=0‎．‎ 设点M(m, 0)‎，则M到直线AP的距离是‎|m+6|‎‎2‎．‎ 于是‎|m+6|‎‎2‎‎=|6-m|‎，又‎-6≤m≤6‎，解得m=2‎，故点M(2, 0)‎．‎ ‎ 5 / 5‎ 设椭圆上的点‎(x, y)‎到点M的距离为d，有 d‎2‎‎=(x-2‎)‎‎2‎+y‎2‎=x‎2‎-4x+4+20-‎5‎‎9‎x‎2‎=‎4‎‎9‎(x-‎9‎‎2‎‎)‎‎2‎+15‎，‎ ‎∴ 当x=‎‎9‎‎2‎时，d取得最小值‎15‎．‎ ‎20.解：（1）设中低价房面积形成数列‎{an}‎，由题意可知‎{an}‎是等差数列，‎ 其中a‎1‎‎=250‎，d=50‎，‎ 则Sn‎=250n+n(n-1)‎‎2‎×50=25n‎2‎+225n，‎ 令‎25n‎2‎+225n≥4750‎，‎ 即n‎2‎‎+9n-190≥0‎，而n是正整数，∴ n≥10‎，‎ ‎∴ 到‎2013‎年底，该市历年所建中低价房的累计面积将首次不少于‎4750‎万平方米．‎ ‎（2）设新建住房面积形成数列‎{bn}‎，由题意可知‎{bn}‎是等比数列，‎ 其中b‎1‎‎=400‎，q=1.08‎，‎ 则bn‎=400⋅(1.08‎‎)‎n-1‎，‎ 由题意可知an‎>0.85‎bn，有‎250+(n-1)⋅50>400⋅(1.08‎)‎n-1‎⋅0.85‎，‎ 由计算器解得满足上述不等式的最小正整数n=6‎，‎ 到‎2009‎年底，当年建造的中低价房的面积占该年建造住房面积的比例首次大于‎85%‎．‎ ‎21.h(x)=x‎2‎x-1‎‎,x∈(-∞,1)∪(1,+∞)‎‎1,x=1‎ ‎．‎ 当x≠1‎时，h(x)=x‎2‎x-1‎=x-1+‎1‎x-1‎+2‎，‎ 若x>1‎时，则h(x)≥4‎，其中等号当x＝‎2‎时成立 若x<1‎时，则h(x)≤0‎，其中等号当x＝‎0‎时成立 ‎∴ 函数h(x)‎的值域是‎(-∞, 0]∪{1}∪[4, +∞)‎ 令f(x)‎＝sin2x+cos2x，‎α=‎π‎4‎ 则g(x)‎＝f(x+α)‎＝sin2(x+π‎4‎)+cos2(x+π‎4‎)‎＝cos2x-sin2x，‎ 于是h(x)‎＝f(x)⋅f(x+α)‎＝‎(sin2x+cos2x)(cos2x-sin2x)‎＝cos4x．‎ 另解令f(x)‎＝‎1+‎2‎sin2x，α=‎π‎2‎，‎ g(x)‎‎＝f(x+α)‎＝‎1+‎2‎sin2(x+π)‎＝‎1-‎2‎sin2x，‎ 于是h(x)‎＝f(x)⋅f(x+α)‎＝‎(1+‎2‎sin2x)(1-‎2‎sin2x)‎＝cos4x．‎ ‎22.解：（1）设点A‎0‎‎(x, y)‎，A‎1‎为A‎0‎关于点P‎1‎的对称点，A‎1‎的坐标为‎(2-x, 4-y)‎，‎ A‎1‎为P‎2‎关于点的对称点A‎2‎的坐标为‎(2+x, 4+y)‎，‎ ‎∴ A‎0‎A‎2‎‎→‎‎={2, 4}‎．‎ ‎（2）∵ A‎0‎A‎2‎‎→‎‎={2, 4}‎，‎ ‎∴ f(x)‎的图象由曲线C向右平移‎2‎个单位，再向上平移‎4‎个单位得到．‎ 因此，设曲线C是函数y=g(x)‎的图象，‎ 其中g(x)‎是以‎3‎为周期的周期函数，‎ 且当x∈(-2, 1]‎时，g(x)=lg(x+2)-4‎．‎ 于是，当x∈(1, 4]‎时，g(x)=lg(x-1)-4‎．‎ ‎（3）A‎0‎An‎→‎‎=A‎0‎A‎2‎‎→‎+A‎2‎A‎4‎‎→‎+...+‎An-2‎An‎→‎，‎ 由于A‎2k-2‎A‎2k‎→‎‎=2‎P‎2k-1‎P‎2k‎→‎，得A‎0‎An‎→‎‎=2(P‎1‎P‎2‎‎→‎+P‎3‎P‎4‎‎→‎+...+Pn-1‎Pn‎→‎)‎ ‎=2({1, 2}+{1, ‎2‎‎3‎}+...+{1, ‎2‎n-1‎})=2{n‎2‎, ‎2(‎2‎n-1)‎‎3‎}={n, ‎4(‎2‎n-1)‎‎3‎}‎ ‎ 5 / 5‎