安徽省六安市第一中学2020届高考适应性考试数学（理）试题 3页

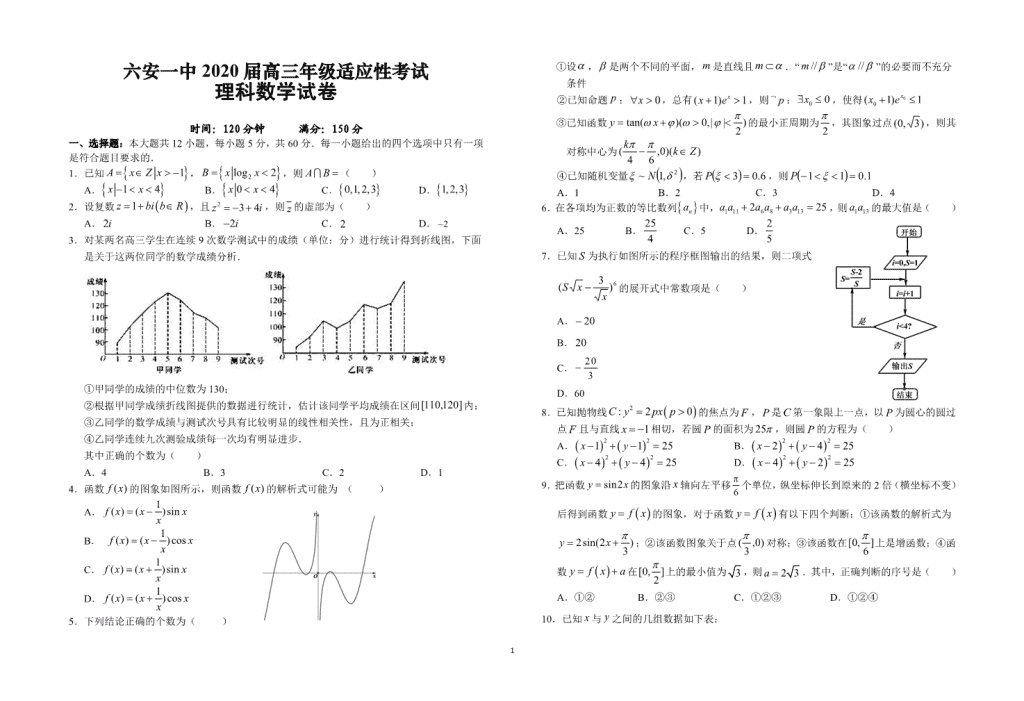
1 六安一中 2020 届高三年级适应性考试 理科数学试卷 时间：120 分钟 满分：150 分 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．每一小题给出的四个选项中只有一项 是符合题目要求的． 1．已知  1A x Z x    ，  2log 2B x x  ，则 A B  （ ） A． 1 4x x   B． 0 4x x  C． 0,1,2,3 D． 1,2,3 2．设复数  1z bi b R   ，且 2 3 4z i   ，则 z 的虚部为（ ） A． 2i B． 2i C． 2 D． 2 3．对某两名高三学生在连续 9 次数学测试中的成绩（单位：分）进行统计得到折线图，下面 是关于这两位同学的数学成绩分析． ①甲同学的成绩的中位数为 130； ②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间 ]120,110[ 内； ③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关； ④乙同学连续九次测验成绩每一次均有明显进步． 其中正确的个数为（ ） A．4 B．3 C．2 D．1 4．函数 )(xf 的图象如图所示，则函数 )(xf 的解析式可能为 （ ） A． 1( ) ( )sinf x x xx   B． 1( ) ( )cosf x x xx   C． 1( ) ( )sinf x x xx   D． 1( ) ( )cosf x x xx   5．下列结论正确的个数为（ ） ①设 ，  是两个不同的平面， m 是直线且 m  ．“ //m ”是“  // ”的必要而不充分 条件 ②已知命题 p ： 0x  ，总有( 1) 1xx e  ，则 p﹁ ： 0 0x  ，使得 0 0( 1) 1xx e  ③已知函数 )2||,0)(tan(   xy 的最小正周期为 2  ，其图象过点 )3,0( ，则其 对称中心为 ))(0,64( Zkk   ④已知随机变量  2,1~  N ，若   6.03 P ，则   1.011  P A．1 B．2 C．3 D．4 6．在各项均为正数的等比数列 na 中， 1 11 3 136 82 25a a a a a a   ，则 1 13a a 的最大值是（ ） A．25 B． 25 4 C．5 D． 2 5 7．已知 S 为执行如图所示的程序框图输出的结果，则二项式 6)3( x xS  的展开式中常数项是（ ） A． 20 B． 20 C． 20 3  D．60 8．已知抛物线  2: 2 0C y px p  的焦点为 F ，P 是C 第一象限上一点，以 P 为圆心的圆过 点 F 且与直线 1x   相切，若圆 P 的面积为 25 ，则圆 P 的方程为（ ） A．   2 21 1 25x y    B．   2 22 4 25x y    C．   2 24 4 25x y    D．   2 24 2 25x y    9．把函数 sin2y x 的图象沿 x 轴向左平移 6  个单位，纵坐标伸长到原来的 2 倍（横坐标不变） 后得到函数  y f x 的图象，对于函数  y f x 有以下四个判断：①该函数的解析式为 )32sin(2  xy ；②该函数图象关于点 )0,3( 对称；③该函数在 ]6,0[  上是增函数；④函 数  y f x a  在 ]2,0[  上的最小值为 3 ，则 2 3a  ．其中，正确判断的序号是（ ） A．①② B．②③ C．①②③ D．①②④ 10．已知 x 与 y 之间的几组数据如下表： 2 x 1 2 3 4 y 1 m n 4 上表数据中 y 的平均值为 2.5 ，若某同学对 m 赋了三个值分别为1.5，2 ，2.5 得到三 条线性回归直线方程分别为 1 1 2 2 3 3, ,y b x a y b x a y b x a      ，对应的相关系数分别为 1 2 3, ,r r r ，下列结论中错误．．的是（ ） A．三条回归直线有共同交点 B．相关系数中， 2r 最大 C． 1 2b b D． 1 2a a 参考公式：线性回归方程 y bx a  ，其中 1 2 1 ( )( ) ( ) n i i i n i i x x y y b x x          ， a y bx   .相关系数 1 2 2 1 1 ( )( ) ( ) ( ) n i i i n n i i i i x x y y r x x y y            . 11．已知向量 ,a b  满足 1a  ，a 与b 的夹角为 3  ，若对一切实数 x， babax  2 恒成立， 则| |b 的取值范围是（ ） A． ),2 1[  B． ),2 1(  C．[1, ) D．(1, ) 12．若函数   lnf x x x h    ，在区间 ],1[ ee 上任取三个实数 a ，b ，c 均存在以 )(af ， )(bf ， )(cf 为边长的三角形，则实数 h 的取值范围是（ ） A． )11,1(  e B． )3,11(  ee C． ),11(  e D． ),3( e 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分．请将答案填写在答题卷相应位置上． 13．设等差数列 na 的前n 项和 nS ， 4 4a  ， 5 15S  ，若数列 }1{ 1nnaa 的前 m 项和为 2021 2020 ， 则 m  ________． 14．当实数 x，y 满足不等式组       ,43 ,43 ,0 yx yx x 时，恒有  1a x y  ，则实数 a 的取值范围是 _________. 15．已知双曲线   2 2 2 2: 1 , 0x yC a ba b    的左右焦点为 1 2,F F ，过 2F 作 x 轴的垂线与C 相交于 ,A B 两点， BF1 与 y 轴相交于 D ，若 1BF AD ，则双曲线C 的离心率是_________. 16．已知正方体 1 1 1 1ABCD A B C D 的棱长为 2，点 ,M N 分别是棱 1,BC CC 的中点，则点 1A 到平面 AMN 的距离是_________；若动 点 P 在正方形 1 1BCC B (包括边界)内运动，且 1PA // 平面 AMN ， 则线段 1PA 的长度范围是_________. 三、解答题：本大题共 6 小题，共 70 分，解答应写出文字说明， 证明过程或演算步骤． 17．（本小题满分 12 分） ABC 的内角 CBA ,, 的对边分别为 cba ,, 且满足 2, cos (2 )cosa a B c b A   ． （1）求角 A 的大小； （2）求 ABC 周长的范围． 18．（本小题满分 12 分） 如图，在三棱柱 111 CBAABC  中，侧面 11AABB 是菱形，  601BAA , E 是棱 1BB 的中点， CBCA  , F 在线段 AC 上，且 FCAF 2 . （1）证明： //1CB 平面 EFA1 ; （2）若 CBCA  ，平面 CAB 平面 11AABB ， 求二面角 AEAF  1 的余弦值. 3 19．（本小题满分 12 分） 已知 D 为圆 24)2(: 22  yxE 上一动点， )0,2(F ，DF 的垂直平分线交 DE 于点 P , 设点 P 的轨迹为曲线 1C . （1）求曲线 1C 的轨迹方程； （2）经过点 )1,0(M 且斜率存在的直线 l 交曲线 1C 于 Q、N 两点，点 B 与点 Q 关于坐标原点对 称，曲线 1C 与 y 轴负半轴交于点 A，连接 AB、AN，是否存在实数  使得对任意直线 l 都有 ABAN kk  成立？若存在，求出 的值；若不存在，请说明理由. 20．（本小题满分 12 分） 已知函数 ).1(log)( 2  akxxxf a （1）讨论 )(xf 单调性； （2）取 ea  ，若 |)(| x xfy  在 ],1[ e 上单调递增，求 k 的取值范围. 21．（本小题满分 12 分） 某项比赛中甲、乙两名选手将要进行决赛，比赛实行五局三胜制.已知每局比赛中必决出 胜负，若甲先发球，其获胜的概率为 2 1 ，否则其获胜的概率为 3 1 . （1）若在第一局比赛中采用掷硬币的方式决定谁先发球，试求甲在此局获胜的概率； （2）若第一局由乙先发球，以后每局由负方发球.规定胜一局得 3 分，负一局得 0 分，记 X 为 比赛结束时甲的总得分，求随机变量 X 的分布列和数学期望. 注意：以下请考生在 22、23 两题中任选一题作答，如果多做，则按所做的第一题记分. 22．（本小题满分 10 分）选修 4-4：坐标系与参数方程 在直角坐标系 xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的 参数方程为        sin2 cos22 y x （ 为参数），直线l 经过点 )33,1( M 且倾斜角为 . （1）求曲线C 的极坐标方程和直线l 的参数方程； （2）已知直线l 与曲线C 交于 BA, 两点，满足 A 为 MB 的中点，求 tan . 23．（本小题满分 10 分）选修 4-5：不等式选讲 已知  Rmmmxxf  2)( . （1）若不等式 2)( xf 的解集为 ]2 3,2 1[ ，求 m 的值； （2）在（1）的条件下，若 ,,,  Rcba 且 mcba  4 ，求证： abcabbcac 3644  .