2014高考山东（理科数学）试卷 12页

‎2014·山东卷(理科数学)‎ ‎1．[2014·山东卷] 已知a，b∈R，i是虚数单位，若a－i与2＋bi互为共轭复数，则(a＋bi)2＝(　　)‎ ‎　　　　　　　　　　　　　　　‎ A．5－4iB．5＋4iC．3－4iD．3＋4i ‎1．D　[解析]因为a－i与2＋bi互为共轭复数，所以a＝2，b＝1，所以(a＋bi)2＝(2＋i)2＝3＋4i.故选D.‎ ‎2．，[2014·山东卷] 设集合A＝{x||x－1|＜2}，B＝{y|y＝2x，x∈[0，2]}，则A∩B＝(　　)‎ A．[0，2] B．(1，3) C．[1，3) D．(1，4)‎ ‎2．C　[解析]根据已知得，集合A＝{x|－1＜x＜3}，B＝{y|1≤y≤4}，所以A∩B＝{x|1≤x＜3}．故选C.‎ ‎3．，[2014·山东卷] 函数f(x)＝的定义域为(　　)‎ A.B．(2，＋∞)‎ C.∪(2，＋∞) D.∪[2，＋∞)‎ ‎3．C　[解析]根据题意得，解得故选C.‎ ‎4．[2014·山东卷] 用反证法证明命题“设a，b为实数，则方程x2＋ax＋b＝0至少有一个实根”时，要做的假设是(　　)‎ A.方程x2＋ax＋b＝0没有实根 B.方程x2＋ax＋b＝0至多有一个实根 C.方程x2＋ax＋b＝0至多有两个实根 D.方程x2＋ax＋b＝0恰好有两个实根 ‎4．A　[解析]“方程x2＋ax＋b＝0至少有一个实根”等价于“方程x2＋ax＋b＝0有一个实根或两个实根”，所以该命题的否定是“方程x2＋ax＋b＝0没有实根”．故选A.‎ ‎5．，，[2014·山东卷] 已知实数x，y满足ax＜ay(0＜a＜1)，则下列关系式恒成立的是(　　)‎ A.＞B.ln(x2＋1)＞ln(y2＋1) ‎ C.sinx＞sinyD.x3＞y3‎ ‎5．D　[解析]因为ax＜ay(0＜a＜1)，所以x＞y，所以sinx＞siny，ln(x2＋1)＞ln(y2＋1)，＞都不一定正确，故选D.‎ ‎6．[2014·山东卷] 直线y＝4x与曲线y＝x3在第一象限内围成的封闭图形的面积为(　　)‎ A.2　B.4　C.2D.4‎ ‎6．D　[解析]直线y＝4x与曲线y＝x3在第一象限的交点坐标是(2，8)，所以两者围成的封闭图形的面积为(4x－x3)dx＝0＝4，故选D.‎ ‎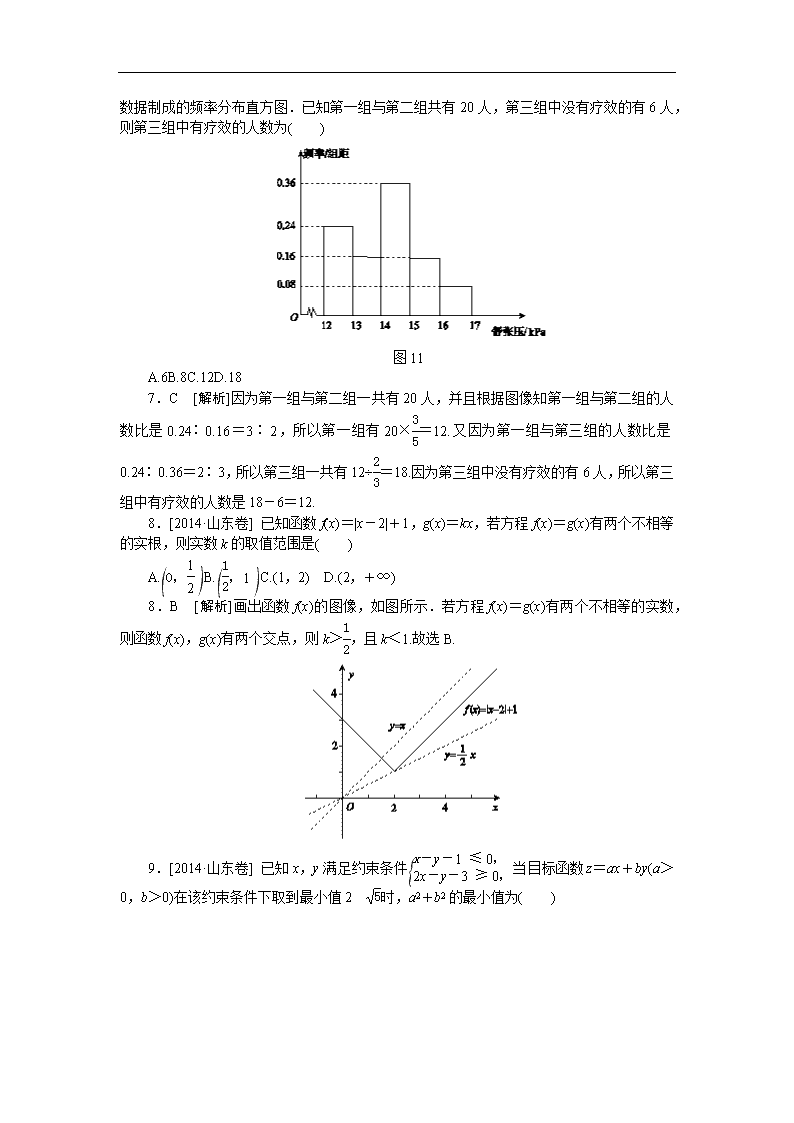7．[2014·山东卷] 为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据(单位：kPa)的分组区间为[12，13)，[13，14)，[14，15)，[15，16)，[16，17]，将其按从左到右的顺序分别编号为第一组，第二组，……，第五组．‎ 下图是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为(　　)‎ 图11‎ A.6B.8C.12D.18‎ ‎7．C　[解析]因为第一组与第二组一共有20人，并且根据图像知第一组与第二组的人数比是0.24∶0.16＝3∶2，所以第一组有20×＝12.又因为第一组与第三组的人数比是0.24∶0.36＝2∶3，所以第三组一共有12÷＝18.因为第三组中没有疗效的有6人，所以第三组中有疗效的人数是18－6＝12.‎ ‎8．[2014·山东卷] 已知函数f(x)＝|x－2|＋1，g(x)＝kx，若方程f(x)＝g(x)有两个不相等的实根，则实数k的取值范围是(　　)‎ A.B.C.(1，2) D.(2，＋∞)‎ ‎8．B　[解析]画出函数f(x)的图像，如图所示．若方程f(x)＝g(x)有两个不相等的实数，则函数f(x)，g(x)有两个交点，则k＞，且k＜1.故选B.‎ ‎9．[2014·山东卷] 已知x，y满足约束条件当目标函数z＝ax＋by(a＞0，b＞0)在该约束条件下取到最小值2　时，a2＋b2的最小值为(　　)‎ A.5B.4C.D.2‎ ‎9．B　[解析]画出约束条件表示的可行域(如图所示)．‎ 显然，当目标函数z＝ax＋by过点A(2，1)时，z取得最小值，即2　＝2a＋b，所以2　－2a＝b，所以a2＋b2＝a2＋(2　－2a)2＝5a2－8　a＋20，构造函数m(a)＝5a2－8　a＋20(>a>0)，利用二次函数求最值，显然函数m(a)＝5a2－8a＋20的最小值是＝4，即a2＋b2的最小值为4.故选B.‎ ‎10．，[2014·山东卷] 已知a＞b＞0，椭圆C1的方程为＋＝1，双曲线C2的方程为－＝1，C1与C2的离心率之积为，则C2的渐近线方程为(　　)‎ A.x±y＝0B.x±y＝0‎ C.x±2y＝0D.2x±y＝0‎ ‎10．A　[解析]椭圆C1的离心率e1＝，双曲线C2的离心率e2＝.由e1e2＝·＝×＝，‎ 解得＝，所以＝，所以双曲线C2的渐近线方程是y＝±x.故选A.‎ ‎11．[2014·山东卷] 执行如图12所示的程序框图，若输入的x的值为1，则输出的n的值为____．‎ 图12‎ ‎11．3　[解析]x＝1满足不等式，执行循环后，x＝2，n＝1；x＝2满足不等式，执行循环后，x＝3，n＝2；x＝3满足不等式，执行循环后，x＝4，n＝3；x＝4不满足不等式，结束循环，输出的n的值为3.‎ ‎12．，[2014·山东卷] 在△ABC中，已知·＝tanA，当A＝时，△ABC的面积为______．‎ ‎12.　[解析]因为AB·AC＝||·||cosA＝tanA，且A＝，所以||·||＝，所以△ABC的面积S＝||·||sinA＝××sin＝.‎ ‎13．[2014·山东卷] 三棱锥PABC中，D，E分别为PB，PC的中点，记三棱锥DABE的体积为V1，PABC的体积为V2，则＝________．‎ ‎13.　[解析]如图所示，由于D，E分别是边PB与PC的中点，所以S△BDE＝S△PBC.又因为三棱锥ABDE与三棱锥APBC的高长度相等，所以＝.‎ ‎14．，[2014·山东卷] 若的展开式中x3项的系数为20，则a2＋b2的最小值为________．‎ ‎14．2　[解析]Tr＋1＝C(ax2)6－r·＝Ca6－r·brx12－3r，令12－3r＝3，得r＝3，所以Ca6－3b3＝20，即a3b3＝1，所以ab＝1，所以a2＋b2≥2ab＝2，当且仅当a＝b，且ab＝1时，等号成立．故a2＋b2的最小值是2.‎ ‎15．[2014·山东卷] 已知函数y＝f(x)(x∈R)，对函数y＝g(x)(x∈I)，定义g(x)关于f(x)的“对称函数”为函数y＝h(x)(x∈I)，y＝h(x)满足：对任意x∈I，两个点(x，h(x))，(x，g(x))关于点(x，f(x))对称．若h(x)是g(x)＝关于f(x)＝3x＋b的“对称函数”，且h(x)＞g(x)恒成立，则实数b的取值范围是________．‎ ‎15．(2，＋∞)　[解析]g(x)的图像表示圆的一部分，即x2＋y2＝4(y≥0)．当直线y＝3x＋b与半圆相切时，满足h(x)>g(x)，根据圆心(0，0)到直线y＝3x＋b的距离是圆的半径求得＝2，解得b＝2或b＝－2(舍去)，要使h(x)>g(x)恒成立，则b＞2，即实数b的取值范围是(2，＋∞)．‎ ‎16．，[2014·山东卷] 已知向量a＝(m，cos2x)，b＝(sin2x，n)，函数f(x)＝a·b，且y＝f(x)的图像过点和点.‎ ‎(1)求m，n的值；‎ ‎(2)将y＝f(x)的图像向左平移φ(0＜φ＜π)个单位后得到函数y＝g(x)的图像，若y＝g(x)图像上各最高点到点(0，3)的距离的最小值为1，求y＝g(x)的单调递增区间．‎ ‎16．解：(1)由题意知，f(x)＝a·b＝msin2x＋ncos2x.‎ 因为y＝f(x)的图像过点和点，‎ 所以 即 解得m＝，n＝1.‎ ‎(2)由(1)知f(x)＝sin2x＋cos2x＝2sin.‎ 由题意知，g(x)＝f(x＋φ)＝2sin.‎ 设y＝g(x)的图像上符合题意的最高点为(x0，2)．‎ 由题意知，x＋1＝1，所以x0＝0，‎ 即到点(0，3)的距离为1的最高点为(0，2)．‎ 将其代入y＝g(x)得，sin＝1.‎ 因为0<φ<π，所以φ＝.‎ 因此，g(x)＝2sin＝2cos2x.‎ 由2kπ－π≤2x≤2kπ，k∈Z得kπ－≤x≤kπ，k∈Z，‎ 所以函数y＝g(x)的单调递增区间为，k∈Z.‎ ‎17．，[2014·山东卷] 如图13所示，在四棱柱ABCDA1B1C1D1中，底面ABCD是等腰梯形，∠DAB＝60°，AB＝2CD＝2，M是线段AB的中点．‎ 图13‎ ‎(1)求证：C1M∥平面A1ADD1；‎ ‎(2)若CD1垂直于平面ABCD且CD1＝，求平面C1D1M和平面ABCD所成的角(锐角)的余弦值．‎ ‎17．解：(1)证明：因为四边形ABCD是等腰梯形，‎ 且AB＝2CD，所以AB∥DC，‎ 又M是AB的中点，‎ 所以CD∥MA且CD＝MA.‎ 连接AD1.因为在四棱柱ABCDA1B1C1D1中，‎ CD∥C1D1，CD＝C1D1，‎ 所以C1D1∥MA，C1D1＝MA，‎ 所以四边形AMC1D1为平行四边形，‎ 因此，C1M∥D1A.‎ 又C1M⊄平面A1ADD1，D1A⊂平面A1ADD1，‎ 所以C1M∥平面A1ADD1.‎ ‎(2)方法一：连接AC，MC.‎ 由(1)知，CD∥AM且CD＝AM，‎ 所以四边形AMCD为平行四边形，‎ 所以BC＝AD＝MC.‎ 由题意∠ABC＝∠DAB＝60°，‎ 所以△MBC为正三角形，‎ 因此AB＝2BC＝2，CA＝，‎ 因此CA⊥CB.‎ 设C为坐标原点，建立如图所示的空间直角坐标系Cxyz.‎ 所以A(，0，0)，B(0，1，0)，D1(0，0，)．‎ 因此M，‎ 所以＝，＝＝.‎ 设平面C1D1M的一个法向量n＝(x，y，z)，‎ 由得 可得平面C1D1M的一个法向量n＝(1，，1)．‎ 又＝(0，0，)为平面ABCD的一个法向量．‎ 因此cos〈，n〉＝＝，‎ 所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为.‎ 方法二：由(1)知，平面D1C1M∩平面ABCD＝AB，点过C向AB引垂线交AB于点N，连接D1N.‎ 由CD1⊥平面ABCD，可得D1N⊥AB，‎ 因此∠D1NC为二面角C1ABC的平面角．‎ 在Rt△BNC中，BC＝1，∠NBC＝60°，‎ 可得CN＝，‎ 所以ND1＝＝.‎ 在Rt△D1CN中，cos∠D1NC＝＝＝，‎ 所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为.‎ ‎18．，[2014·山东卷] 乒乓球台面被网分隔成甲、乙两部分，如图14所示，甲上有两个不相交的区域A，B，乙被划分为两个不相交的区域C，D.某次测试要求队员接到落点在甲上的来球后向乙回球．规定：回球一次，落点在C上记3分，在D上记1分，其他情况记0分．对落点在A上的来球，队员小明回球的落点在C上的概率为，在D上的概率为；对落点在B上的来球，小明回球的落点在C上的概率为，在D上的概率为.假设共有两次来球且落在A，B上各一次，小明的两次回球互不影响．求：‎ ‎(1)小明两次回球的落点中恰有一次的落点在乙上的概率；‎ ‎(2)两次回球结束后，小明得分之和ξ的分布列与数学期望．‎ 图14‎ ‎18．解：(1)记Ai为事件“小明对落点在A上的来球回球的得分为i分”(i＝0，1，3)，‎ 则P(A3)＝，P(A1)＝，P(A0)＝1－－＝；‎ 记Bi为事件“小明对落点在B上的来球回球的得分为i分”(i＝0，1，3)，‎ 则P(B3)＝，P(B1)＝，P(B0)＝1－－＝.‎ 记D为事件“小明两次回球的落点中恰有1次的落点在乙上”．‎ 由题意，D＝A3B0＋A1B0＋A0B1＋A0B3，‎ 由事件的独立性和互斥性，‎ P(D)＝P(A3B0＋A1B0＋A0B1＋A0B3)‎ ‎＝P(A3B0)＋P(A1B0)＋P(A0B1)＋P(A0B3)‎ ‎＝P(A3)P(B0)＋P(A1)P(B0)＋P(A0)·P(B1)＋P(A0)P(B3)‎ ‎＝×＋×＋×＋× ‎＝，‎ 所以小明两次回球的落点中恰有1次的落点在乙上的概率为.‎ 由题意，随机变量ξ可能的取值为0，1，2，3，4，6.‎ ‎(2)由事件的独立性和互斥性，得 P(ξ＝0)＝P(A0B0)＝×＝，‎ P(ξ＝1)＝P(A1B0＋A0B1)＝P(A1B0)＋P(A0B1)＝×＋×＝，‎ P(ξ＝2)＝P(A1B1)＝×＝，‎ P(ξ＝3)＝P(A3B0＋A0B3)＝P(A3B0)＋P(A0B3)＝×＋×＝，‎ P(ξ＝4)＝P(A3B1＋A1B3)＝P(A3B1)＋P(A1B3)＝×＋×＝，‎ P(ξ＝6)＝P(A3B3)＝×＝.‎ 可得随机变量ξ的分布列为：‎ ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎6‎ P 所以数学期望Eξ＝0×＋1×＋2×＋3×＋4×＋6×＝.‎ ‎19．，，[2014·山东卷] 已知等差数列{an}的公差为2，前n项和为Sn，且S1，S2，S4成等比数列．‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)令bn＝(－1)n－1，求数列{bn}的前n项和Tn.‎ ‎19．解： (1)因为S1＝a1，S2＝2a1＋×2＝2a1＋2，‎ S4＝4a1＋×2＝4a1＋12，‎ 由题意得(2a1＋2)2＝a1(4a1＋12)，解得a1＝1，‎ 所以an＝2n－1.‎ ‎(2)由题意可知，‎ bn＝(－1)n－1 ‎＝(－1)n－1 ‎＝(－1)n－1.‎ 当n为偶数时，‎ Tn＝－＋…＋－ ‎＝1－ ‎＝.‎ 当n为奇数时，‎ Tn＝－＋…－＋ ‎＝1＋ ‎＝.‎ 所以Tn＝ ‎20．[2014·山东卷] 设函数f(x)＝－k(k为常数，e＝2.71828…是自然对数的底数)．‎ ‎(1)当k≤0时，求函数f(x)的单调区间；‎ ‎(2)若函数f(x)在(0，2)内存在两个极值点，求k的取值范围．‎ ‎20．解：(1)函数y＝f(x)的定义域为(0，＋∞)，‎ f′(x)＝－k ‎＝－ ‎＝.‎ 由k≤0可得ex－kx>0，‎ 所以当x∈(0，2)时，f′(x)<0，函数y＝f(x)单调递减；x∈(2，＋∞)时，f′(x)>0，函数y＝f(x)单调递增．‎ 所以f(x)的单调递减区间为(0，2)，单调递增区间为(2，＋∞)．‎ ‎(2)由(1)知，当k≤0时，函数f(x)在(0，2)内单调递减，故f(x)在(0，2)内不存在极值点；‎ 当k>0时，设函数g(x)＝ex－kx，x∈(0，＋∞)．‎ 因为g′(x)＝ex－k＝ex－elnk，‎ 当00，y＝g(x)单调递增，‎ 故f(x)在(0，2)内不存在两个极值点．‎ 当k>1时，得x∈(0，lnk)时，g′(x)<0，函数y＝g(x)单调递减；‎ x∈(lnk，＋∞)时，g′(x)>0，函数y＝g(x)单调递增．‎ 所以函数y＝g(x)的最小值为g(lnk)＝k(1－lnk)．‎ 函数f(x)在(0，2)内存在两个极值点．‎ 当且仅当 解得e0)，则FD的中点为.‎ 因为|FA|＝|FD|，‎ 由抛物线的定义知3＋＝，‎ 解得t＝3＋p或t＝－3(舍去)．‎ 由＝3，解得p＝2，‎ 所以抛物线C的方程为y2＝4x.‎ ‎(2)①证明：由(1)知F(1，0)．‎ 设A(x0，y0)(x0y0≠0)，D(xD，0)(xD>0)．‎ 因为|FA|＝|FD|，则|xD－1|＝x0＋1，‎ 由xD>0得xD＝x0＋2，故D(x0＋2，0)．‎ 故直线AB的斜率kAB＝－.‎ 因为直线l1和直线AB平行，‎ 设直线l1的方程为y＝－x＋b，‎ 代入抛物线方程得y2＋y－＝0，‎ 由题意Δ＝＋＝0，得b＝－.‎ 设E(xE，yE)，则yE＝－，xE＝.‎ 当y≠4时，kAE＝＝－＝，‎ 可得直线AE的方程为y－y0＝(x－x0)，‎ 由y＝4x0，‎ 整理可得y＝(x－1)，‎ 直线AE恒过点F(1，0)．‎ 当y＝4时，直线AE的方程为x＝1，过点F(1，0)．‎ 所以直线AE过定点F(1，0)．‎ ‎②由①知，直线AE过焦点F(1，0)，‎ 所以|AE|＝|AF|＋|FE|＝(x0＋1)＋＝x0＋＋2.‎ 设直线AE的方程为x＝my＋1，‎ 因为点A(x0，y0)在直线AE上，‎ 故m＝.‎ 设B(x1，y1)．‎ 直线AB的方程为y－y0＝－(x－x0)，‎ 由y0≠0，得x＝－y＋2＋x0.‎ 代入抛物线方程得y2＋y－8－4x0＝0，‎ 所以y0＋y1＝－，‎ 可求得y1＝－y0－，x1＝＋x0＋4.‎ 所以点B到直线AE的距离为 d＝ ‎＝ ‎＝4，‎ 则△ABE的面积S＝×4x0＋＋2≥16，‎ 当且仅当＝x0，即x0＝1时，等号成立．‎ 所以△ABE的面积的最小值为16.‎