专题05+函数﹑基本初等函数的图像与性质（仿真押题）-2019年高考数学（文）命题猜想与仿真押题 8页

‎1．函数y＝的定义域是(　　)‎ A．(－1，＋∞)　　　　B．[－1，＋∞)‎ C．(－1,2)∪(2，＋∞) D．[－1,2)∪(2，＋∞)‎ ‎【解析】选C.由题意知，要使函数有意义，需，即－1＜x＜2或x＞2，所以函数的定义域为(－1,2)∪(2，＋∞)．故选C. ‎ ‎11．函数y＝的定义域为(　　) ‎ A．[1，＋∞)　　　　　　　 B．(1，＋∞)‎ C. D. ‎【解析】由log3(2x－1)≥0得2x－1≥1，x≥1.因此函数的定义域是[1，＋∞)，故选A.‎ ‎【答案】A ‎12．已知函数f(x)＝则f(f(4))的值为(　　)‎ A．－ B．－9‎ C. D．9‎ ‎【答案】C ‎13．函数y＝lg|x|(　　)‎ A．是偶函数，在区间(－∞，0)上单调递增 B．是偶函数，在区间(－∞，0)上单调递减 C．是奇函数，在区间(0，＋∞)上单调递增 D．是奇函数，在区间(0，＋∞)上单调递减 ‎【解析】因为lg|－x|＝lg|x|，所以函数y＝lg|x|为偶函数，又函数y＝lg|x|在区间(0，＋∞)上单调递增，由其图象关于y轴对称，可得y＝lg|x|在区间(－∞，0)上单调递减，故选B.‎ ‎【答案】B ‎14．函数f(x)＝2|log2x|－的图象为(　　)‎ ‎【答案】D ‎15．对于函数y＝f(x)，部分x与y的对应关系如下表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8 ‎ ‎9‎ y ‎3‎ ‎7‎ ‎5‎ ‎9‎ ‎6‎ ‎1‎ ‎8‎ ‎2‎ ‎4‎ 数列{xn}满足：x1＝1，且对于任意n∈N*，点(xn，xn＋1)都在函数y＝f(x)的图象上，则x1＋x2＋…＋x2 017＝(　　)‎ A．7 554 B．7 540‎ C．7 561 D．7 564‎ ‎【解析】∵数列{xn}满足x1＝1，且对任意n∈N*，点(xn，xn＋1)都在函数y＝f(x)的图象上，∴xn＋1＝f(xn)，‎ ‎∴由图表可得x2＝f(x1)＝3，x3＝f(x2)＝5，x4＝f(x3)＝6，x5＝f(x4)＝1，…，∴数列{xn}是周期为4的周期数列，∴x1＋x2＋…＋x2 017＝504(x1＋x2＋x3＋x4)＋x1＝504×15＋1＝7 561.故选C.‎ ‎【答案】C ‎16．已知函数y＝sin ax＋b(a>0)的图象如图所示，则函数y＝loga(x＋b)的图象可能是(　　)‎ ‎【解析】由题图可知00恒成立．设a＝f(－4)，b＝‎ f(1)，c＝f(3)，则a，b，c的大小关系为(　　)‎ A．a0，故函数f(x)在(0，＋∞)上单调递增，故f(－4)＝f(4)>f(3)>f(1)，即a>c>b，故选C. 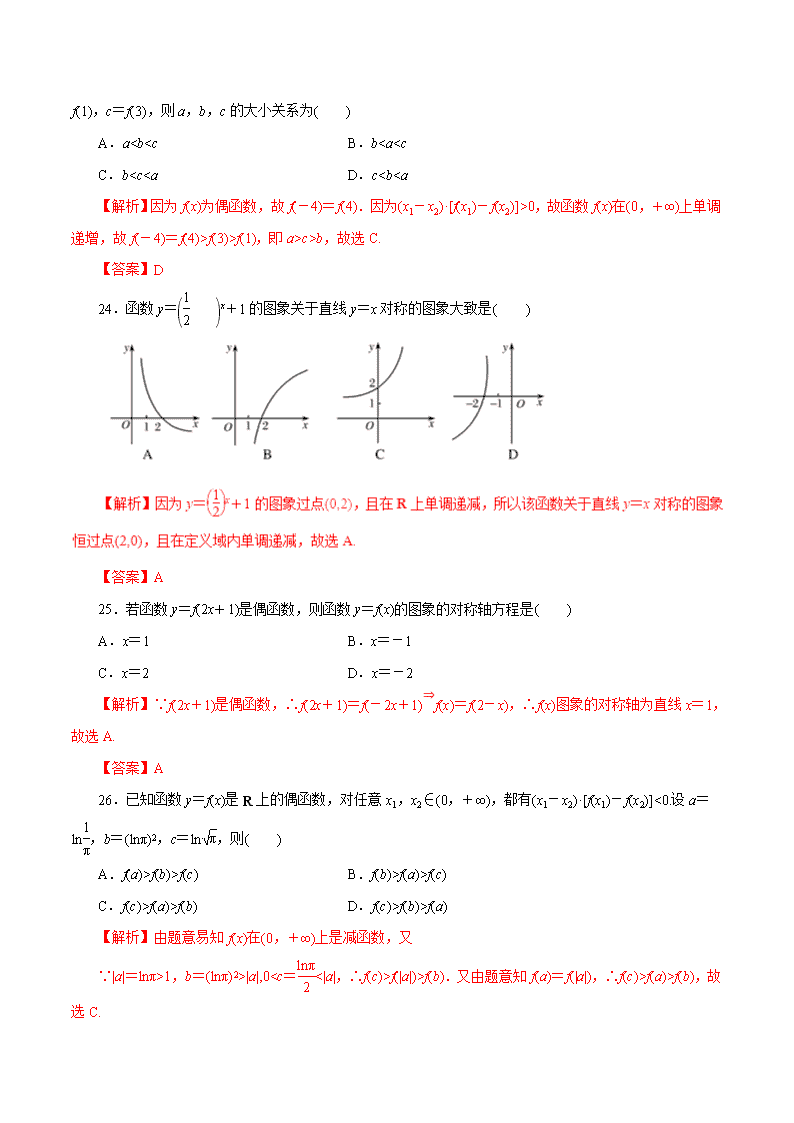‎ ‎【答案】D ‎24．函数y＝x＋1的图象关于直线y＝x对称的图象大致是(　　)‎ ‎【答案】A ‎25．若函数y＝f(2x＋1)是偶函数，则函数y＝f(x)的图象的对称轴方程是(　　)‎ A．x＝1 B．x＝－1‎ C．x＝2 D．x＝－2‎ ‎【解析】∵f(2x＋1)是偶函数，∴f(2x＋1)＝f(－2x＋1)⇒f(x)＝f(2－x)，∴f(x)图象的对称轴为直线x＝1，故选A.‎ ‎【答案】A ‎26．已知函数y＝f(x)是R上的偶函数，对任意x1，x2∈(0，＋∞)，都有(x1－x2)·[f(x1)－f(x2)]<0.设a＝ln，b＝(lnπ)2，c＝ln，则(　　)‎ A．f(a)>f(b)>f(c) B．f(b)>f(a)>f(c)‎ C．f(c)>f(a)>f(b) D．f(c)>f(b)>f(a)‎ ‎【解析】由题意易知f(x)在(0，＋∞)上是减函数，又 ‎∵|a|＝lnπ>1，b＝(lnπ)2>|a|,0f(|a|)>f(b)．又由题意知f(a)＝f(|a|)，∴f(c)>f(a)>f(b)，故选C.‎ ‎【答案】C ‎27． “a≤0”是“函数f(x)＝|(ax－1)x|在(0，＋∞)内单调递增”的(　　)‎ A．充分不必要条件 ‎ B．必要不充分条件 C．充分必要条件 ‎ D．既不充分也不必要条件 ‎【答案】C ‎28．函数f(x)＝＋ln|x|的图象大致为(　　)‎ ‎【解析】当x<0时，函数f(x)＝＋ln(－x)，易知函数f(x)＝＋ln(－x)在(－∞，0)上递减，排除C，D；当x>0时，函数f(x)＝＋lnx，f(2)＝＋ln2≠2，故排除A，故选B. ‎ ‎【答案】－2‎ ‎37.若函数f(x)＝有两个不同的零点，则实数a的取值范围是________.‎ ‎【解析】当x＞0时，由f(x)＝ln x＝0，得x＝1.‎ 因为函数f(x)有两个不同的零点，则当x≤0时，‎ 函数f(x)＝2x－a有一个零点，令f(x)＝0得a＝2x，‎ 因为0＜2x≤20＝1，所以0＜a≤1，‎ 所以实数a的取值范围是0＜a≤1.‎ ‎【答案】(0，1]‎ ‎38.已知函数y＝f(x)是R上的偶函数，对x∈R都有f(x＋4)＝f(x)＋f(2)成立.当x1，x2∈[0，2]，且x1≠x2时，都有＜0，给出下列命题：‎ ‎①f(2)＝0；‎ ‎②直线x＝－4是函数y＝f(x)图象的一条对称轴；‎ ‎③函数y＝f(x)在[－4，4]上有四个零点；‎ ‎④f(2 014)＝0.‎ 其中所有正确命题的序号为________.‎ ‎【答案】①②④‎ ‎39.定义在[－1，1]上的奇函数f(x)，已知当x∈[－1，0]时，f(x)＝－(a∈R).‎ ‎(1)写出f(x)在[0，1]上的解析式；‎ ‎(2)求f(x)在[0，1]上的最大值.‎ ‎【解析】(1)∵f(x)是定义在[－1，1]上的奇函数，‎ ‎∴f(0)＝0，∴a＝1， ‎ ‎42．已知函数f(x)＝x2＋(x≠0，a∈R)．‎ ‎(1)判断函数f(x)的奇偶性；‎ ‎(2)若f(x)在区间[2，＋∞)上是增函数，求实数a的取值范围．‎ ‎43．f(x)的定义域为R，对任意x，y∈R，有f(x＋y)＝f(x)＋f(y)，且当x＞0时，f(x)＜0，f(1)＝－2. ‎ ‎(1)证明：f(x)是奇函数；‎ ‎(2)证明：f(x)在R上是减函数；‎ ‎(3)求f(x)在区间[－3，3]上的最大值和最小值．‎ ‎【解析】(1)函数f(x)的定义域R关于原点对称，又由f(x＋y)＝f(x)＋f(y)，‎ 得f[x＋(－x)]＝f(x)＋f(－x)，‎ ‎∴f(x)＋f(－x)＝f(0)．‎ 又f(0＋0)＝f(0)＋f(0)，‎ ‎∴f(0)＝0.从而有f(x)＋f(－x)＝0，‎ ‎∴f(－x)＝－f(x)．由于x∈R，‎ ‎∴f(x)是奇函数．‎ ‎44．已知函数f(x)＝ex－e－x(x∈R，且e为自然对数的底数)．‎ ‎(1)判断函数f(x)的奇偶性与单调性．‎ ‎(2)是否存在实数t，使不等式f(x－t)＋f(x2－t2)≥0对一切x都成立？若存在，求出t；若不存在，请说明理由．‎ ‎【解析】(1)∵f(x)＝ex－，且y＝ex是增函数，‎ y＝－是增函数，∴f(x)是增函数．‎ ‎∵f(x)的定义域为R，‎ 且f(－x)＝e－x－ex＝－f(x)，‎ ‎∴f(x)是奇函数．‎ ‎(2)由(1)知f(x)是增函数和奇函数，‎ 由f(x－t)＋f(x2－t2)≥0对x∈R恒成立，‎ 则f(x－t)≥f(t2－x2)．‎ ‎∴t2－x2≤x－t⇔x2＋x≥t2＋t对x∈R恒成立⇔≤min对一切x∈R恒成立⇔≤0⇔t＝－.‎ 即存在实数t＝－，使不等式f(x－t)＋f(x2－t2)≥0对一切x都成立．‎ ‎ ‎ ‎ ‎