2021届新高考版高考数学一轮复习课件：§5-3　三角函数的图象、性质及应用（讲解部分） 23页

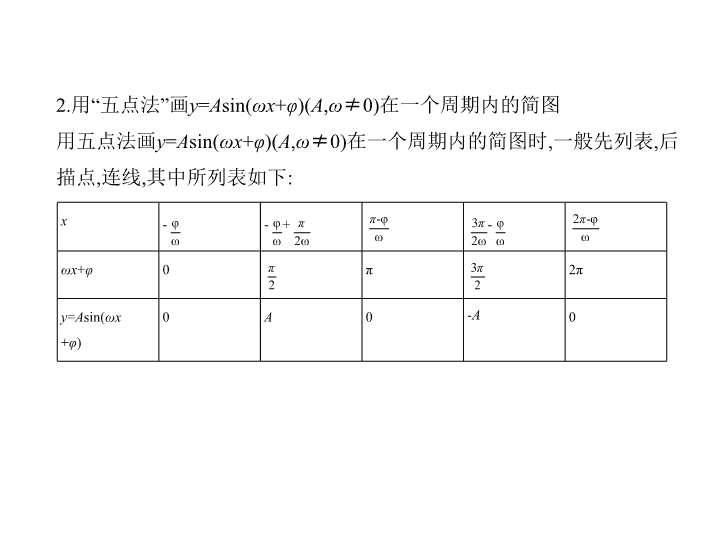
考点一　三角函数的图象及其变换 1.用五点法作正弦函数和余弦函数的简图 (1)正弦函数 y =sin x , x ∈[0,2π]的图象中,五个关键点:(0,0),   ,(π,0), ①             ,(2π,0). (2)余弦函数 y =cos x , x ∈[0,2π]的图象中,五个关键点:(0,1),   ,② 　(π,-1)     ,   ,(2π,1). 考点清单 x -   -   +       -     ωx + φ 0   π   2π y = A sin( ωx + φ ) 0 A 0 - A 0 2. 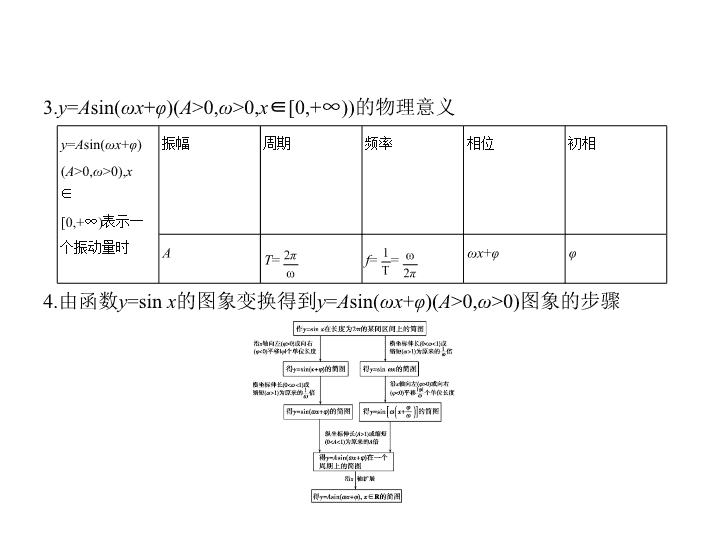用“五点法”画 y = A sin( ωx + φ )( A , ω ≠ 0) 在一个周期内的简图 用五点法画 y = A sin( ωx + φ )( A , ω ≠ 0) 在一个周期内的简图时 , 一般先列表 , 后 描点 , 连线 , 其中所列表如下 : 3. y = A sin( ωx + φ )( A >0, ω >0, x ∈[0,+ ∞ ))的物理意义 4.由函数 y =sin x 的图象变换得到 y = A sin( ωx + φ )( A >0, ω >0)图象的步骤 y = A sin( ωx + φ ) ( A >0, ω >0), x ∈ [0,+ ∞ )表示一 个振动量时 振幅 周期 频率 相位 初相 A T =   f =   =   ωx + φ φ 上述两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是| φ |个 单位;而先周期变换(伸缩变换)再相位变换,平移的量是   ( ω >0)个单位.原 因在于相位变换和周期变换都是针对 x 而言的. 特别提醒　 (1)平移前后两个三角函数的名称如果不一致,应先利用诱导公 式化为同名函数. (2) ω 为负时应先变成正值. 考点二 　三角函数的性质及其应用 1.正弦函数、余弦函数、正切函数的图象和性质 函数性质 y =sin x y =cos x y =tan x 定义域 R R   x   x ≠ k π+   , k ∈Z   图象       值域 [-1,1] [-1,1] R 对称性 对称轴: x = k π+   ( k ∈Z);对称中心:( k π,0)( k ∈Z) 对称轴: x = k π( k ∈Z);对称中心: ③             ( k ∈Z) 对称中心:   ( k ∈Z) 周期 2π 2π π 单调性 单调增区间: ④        2 k π-   ,2 k π+          ( k ∈Z); 单调减区间: ⑤        2 k π+   ,2 k π+          ( k ∈Z) 单调增区间: [2 k π-π,2 k π]( k ∈Z); 单调减区间: [2 k π,2 k π+π]( k ∈Z) 单调增区间: ⑥        k π-   , k π+          ( k ∈Z) 奇偶性 奇 偶 奇 2.求三角函数最值的常见函数形式 (1) y = a sin x + b cos x =   sin( x + φ ),其中cos φ =   ,sin φ =   ( a ≠ 0, b ≠ 0). (2) y = a sin 2 x + b cos 2 x + c sin x cos x ( a ≠ 0, b ≠ 0)   y = A sin 2 x + B cos 2 x + C =   ·sin(2 x + φ )+ C ,其中tan φ =   ,再利用有界性处理. (3) y = a sin 2 x + b cos x + c ( a ≠ 0, b ≠ 0)可转化为关于cos x 的二次函数式. (4) y = a sin x +   ( a , b , c >0),令sin x = t ,则转化为求 y = at +   (-1 ≤ t ≤ 1,且 t ≠ 0) 的最值,一般可结合图象求解. (5) y = a (sin x +cos x )+ b sin x ·cos x + c ( a ≠ 0, b ≠ 0)型常用换元法,令 t =sin x +cos x ,| t | ≤   ,则sin x cos x =   ,把三角问题转化为代数问题求解. 特别提醒　(1)正弦曲线和余弦曲线相邻的两个对称轴之间距离的2倍是 一个周期. (2)正弦曲线和余弦曲线相邻两个对称中心之间的距离的2倍是一个周期. (3)正弦曲线和余弦曲线相邻的一个对称轴和一个对称中心之间距离的4 倍是一个周期. (4)正切曲线相邻的两个对称中心之间距离的2倍是一个周期. (5)不能认为 y =tan x 在定义域上为增函数,应在区间   ( k ∈Z)内 为增函数. 考法一 　关于三角函数图象的问题 知能拓展 例1 　(1)(2018广东茂名化州二模,9)已知函数 f ( x )= A sin( ωx + φ )( A >0, ω >0,0< φ <π)的部分图象如图所示,且 f ( α )=1, α ∈   ,则cos   =   (　　) A. ±   　    B.   　    C.-   　    D.   (2)某同学用“五点法”画函数 f ( x )= A sin( ωx + φ )   在某一个周期 内的图象时,列表并填入了部分数据,如表: ωx + φ 0   π   2π x     A sin( ωx + φ ) 0 5 -5 0 　　①请将上表数据补充完整,并直接写出函数 f ( x )的解析式; ②将 y = f ( x )图象上所有点向左平行移动 θ ( θ >0)个单位长度,得到 y = g ( x )的图 象.若 y = g ( x )图象的一个对称中心为   ,求 θ 的最小值. 解题导引 　(1)由图象的最高点,最低点求 A ,由点   ,   求 φ 及 ω ,从而 得到 f ( x )的解析式,由 f ( α )=1求 α ,进而得cos   . (2)①根据已知表格中的数据可得方程组   解之可得函数 f ( x )的 解析式,进而可补全表格. ②由①并结合函数图象平移可得, g ( x )=5sin   .因为 y =sin x 图象的 对称中心为( k π,0), k ∈Z,令2 x +2 θ -   = k π, k ∈Z,解得 x =   +   - θ , k ∈Z,令   +   - θ =   , k ∈Z,解得 θ =   -   , k ∈Z,由 θ >0可知,当 k =1时, θ 取得最小值   . 解析　 (1)由题图可得 A =3,   =4 ×   =π,得 ω =2,故 f ( x )=3sin(2 x + φ ),将   代入可得3sin   =-3,故sin   =-1,∴   + φ =2 k π-   ( k ∈Z),∴ φ =2 k π-   , k ∈Z. 结合0< φ <π可得 φ =   , 故 f ( x )=3sin   . ∵ f ( α )=3sin   =1,∴sin   =   . ∵ α ∈   ,∴2 α +   ∈   , ∴cos   =-   =-   ,故选C. (2)①根据表中已知数据,得 A =5, ω =2, φ =-   .数据补全如表: ωx + φ 0   π   2π x           π A sin( ωx + φ ) 0 5 0 -5 0 且函数解析式为 f ( x )=5sin   . ②由①知 f ( x )=5sin   ,得 g ( x )=5sin   . 因为 y =sin x 图象的对称中心为( k π,0), k ∈Z. 所以令2 x +2 θ -   = k π, k ∈Z,解得 x =   +   - θ , k ∈Z. 由于函数 y = g ( x )的图象关于点   中心对称,所以令   +   - θ =   , k ∈Z,解得 θ =   -   , k ∈Z.由 θ >0可知,当 k =1时, θ 取得最小值   . 答案 　(1)C 方法总结 　1.根据图象确定函数解析式 求函数 y = A sin( ωx + φ )+ B ( A >0, ω >0,| φ |<π)解析式的方法与步骤 (1)求 A 、 B ,确定函数的最大值 M 和最小值 m ,则 A =   , B =   . (2) ω 由周期得到. (3)利用峰点、谷点或零点列出关于 φ 的方程,结合 φ 的范围解得 φ 的值,所列 方程如下: 峰点: ωx + φ =   +2 k π;谷点: ωx + φ =-   +2 k π. 利用零点时,要区分该零点是升零点,还是降零点. 升零点(图象上升时与 x 轴的交点): ωx + φ =2 k π; 降零点(图象下降时与 x 轴的交点): ωx + φ =π+2 k π.(以上 k ∈Z) (1)五点法作图:用“五点法”作 y = A sin( ωx + φ )的简图,主要是通过变量代 换,设 z = ωx + φ ,由 z 取0,   ,π,   π,2π来求出相应的 x ,通过列表,计算得出五点坐 标,描点后得出图象. (2)图象变换法:由函数 y =sin x 的图象通过变换得到 y = A sin( ωx + φ )的图象有 两种途径:“先平移后伸缩”与“先伸缩后平移”. 2.画函数 y = A sin( ωx + φ )( A >0, ω >0)图象的两种常用方法 考法二 　三角函数的单调性问题 例2 　求下列函数的单调区间: (1) y =2sin   的减区间; (2) y =tan   的减区间. 解题导引 　(1)把 x -   作为一个整体代入 y =sin x 的相应单调减区间内,从而 得出函数 y =sin   的减区间. (2)先把 y =tan   化为 y =-tan   ,再把2 x -   作为一个整体代入 y =tan x 的相应增区间内,即可求出 y =tan   的减区间. 解析 　(1)由2 k π+   ≤ x -   ≤ 2 k π+   π, k ∈Z, 得2 k π+   π ≤ x ≤ 2 k π+   π, k ∈Z. ∴函数 y =2sin   的单调减区间为   ( k ∈Z). (2)把函数 y =tan   化为 y =-tan   . 由 k π-   <2 x -   < k π+   , k ∈Z, 得 k π-   <2 x < k π+   π, k ∈Z. ∴   -   < x <   +   π, k ∈Z. ∴函数 y =tan   的单调减区间为   ( k ∈Z). 误区分析 　(2)中若直接由 k π-   <   -2 x < k π+   ( k ∈Z)得 x 的范围,易把单调性 弄错.失误原因是忽视了 y =tan   实质上是 y =tan x 与 y =   -2 x 的复合,应 按复合函数单调性求解. 方法总结 　三角函数的单调性问题的常见类型及解题策略 1.已知三角函数解析式求单调区间 (1)求函数的单调区间应遵循简单化原则,将解析式进行化简,并注意复合 函数单调性规律“同增异减”. (2)求形如 y = A sin( ωx + φ )或 y = A cos( ωx + φ )(其中 ω >0)的单调区间时,要视“ ωx + φ ”为一个整体,通过解不等式求解.如果 ω <0,那么一定先借助诱导公式 将 ω 化为正数. 2.已知三角函数的单调区间求参数,先求出函数的单调区间,然后利用集合 间的关系求解. 考法三 　三角函数的奇偶性、周期性、对称性的有关问题 例3 　若函数 f ( x )=sin   的图象向左平移   个单位后,得到 y = g ( x )的图象, 则下列说法错误的是   (　　) A. y = g ( x )的最小正周期为π B. y = g ( x )的图象关于直线 x =   对称 C. y = g ( x )在   上单调递增 D. y = g ( x )的图象关于点   对称 解析　 把函数 f ( x )=sin   的图象向左平移   个单位后,得到 y = g ( x )=sin   的图象,故 g ( x )的最小正周期为   =π,故A中说法正确;令 x =   ,可得 g ( x )=1,为最大值,故 y = g ( x )的图象关于直线 x =   对称,故B中说法正确;∵ x ∈   ,∴2 x +   ∈   , 易知 y = g ( x )在   上不单调,故C中说法错误; 由 x =   ,可得 g ( x )=0,故 y = g ( x )的图象关于点   对称,故D中说法正确.综 上,选C. 答案     C 方法总结 　1.若 f ( x )= A sin( ωx + φ )( A , ω , φ 为常数, A ≠ 0)为偶函数,则 φ = k π+   ( k ∈Z),同时当 x =0时, f ( x )取得最大值或最小值.若 f ( x )= A sin( ωx + φ )为奇函数, 则 φ = k π( k ∈Z),同时当 x =0时, f ( x )=0. 2.求三角函数的最小正周期,一般先通过三角恒等变换化为 y = A sin( ωx + φ )+ c 或 y = A cos( ωx + φ )+ c 或 y = A tan( ωx + φ )+ c ( A , ω , φ , c 为常数, A ≠ 0)的形式,再分别 应用公式 T =   (正弦、余弦型)或 T =   求解. 3.函数 f ( x )= A sin( ωx + φ )+ c ( A , ω , φ , c 为常数, A ≠ 0)图象的对称轴一定经过图象 的最高点或最低点,对称中心的横坐标一定是函数的零点,因此在判断直线 x = x 0 或点( x 0 ,0)是不是函数图象的对称轴或对称中心时,可通过检验 f ( x 0 )的 值进行判断. 考法四 　三角函数的最值 例4     (2017山东,16,12分)设函数 f ( x )=sin   ωx -     +sin   ,其中0< ω <3. 已知 f   =0. (1)求 ω ; (2)将函数 y = f ( x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再 将得到的图象向左平移   个单位,得到函数 y = g ( x )的图象,求 g ( x )在   上的最小值. 解析 　(1)因为 f ( x )=sin   +sin   , 所以 f ( x )=   sin ωx -   cos ωx -cos ωx =   sin ωx -   cos ωx =     =   sin   . 由题设知 f   =0,所以   -   = k π, k ∈Z. 故 ω =6 k +2, k ∈Z,又0< ω <3,所以 ω =2. (2)由(1)得 f ( x )=   sin   , 所以 g ( x )=   sin   =   sin   . 因为 x ∈   ,所以 x -   ∈   , 当 x -   =-   ,即 x =-   时, g ( x )取得最小值-   .