高中数学人教a版必修三 章末综合测评2 word版含答案 14页

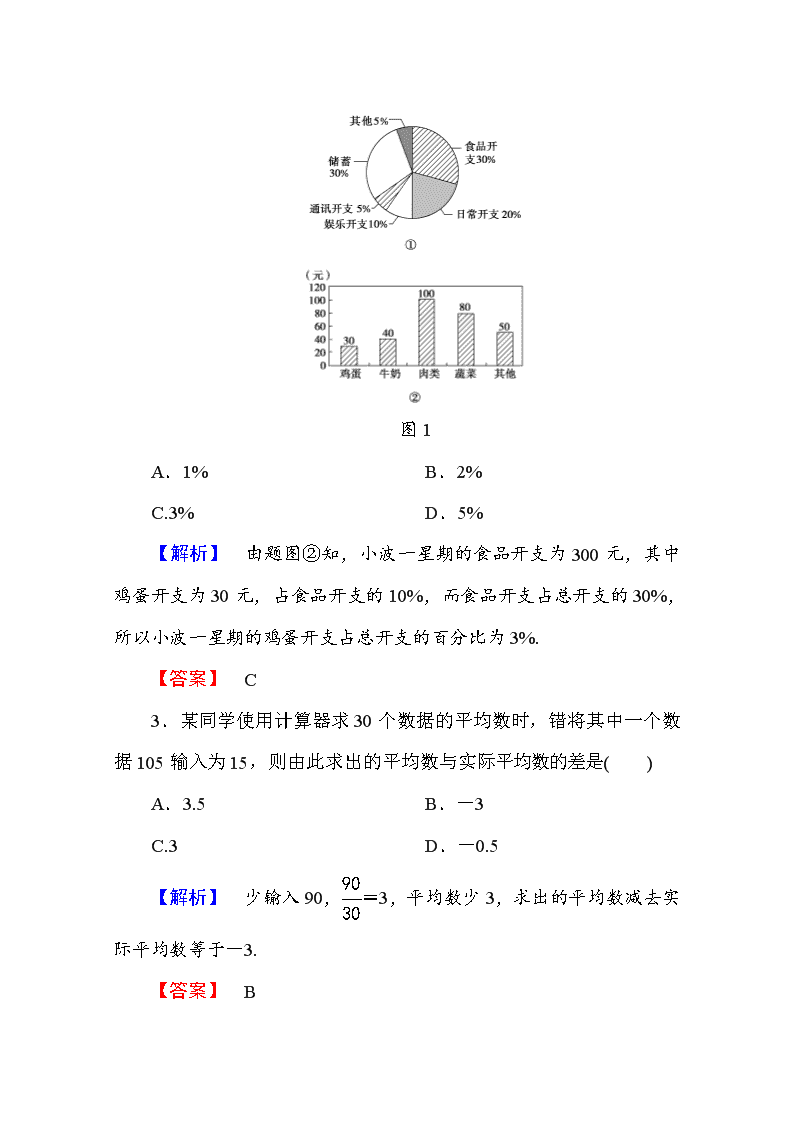
章末综合测评(二) 统计 (时间 120 分钟，满分 150 分) 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分．在每小题 给出的四个选项中，只有一项是符合题目要求的) 1．某学校为了调查高一年级的 200 名学生完成课后作业所需时间， 采取了两种抽样调查的方式：第一种由学生会的同学随机抽取 20 名同 学进行抽查；第二种由教务处对该年级的学生进行编号，从 001 到 200， 抽取学号最后一位为 2 的同学进行调查．则这两种抽样的方法依次是 ( ) A．分层抽样，简单随机抽样 B．简单随机抽样，分层抽样 C．分层抽样，系统抽样 D．简单随机抽样，系统抽样 【解析】 由抽样方法的概念知，第一种是简单随机抽样，第二 种是系统抽样． 【答案】 D 2．小波一星期的总开支分布如图 1①所示，一星期的食品开支如 图 1②所示，则小波一星期的鸡蛋开支占总开支的百分比为( ) 图 1 A．1% B．2% C.3% D．5% 【解析】 由题图②知，小波一星期的食品开支为 300 元，其中 鸡蛋开支为 30 元，占食品开支的 10%，而食品开支占总开支的 30%， 所以小波一星期的鸡蛋开支占总开支的百分比为 3%. 【答案】 C 3．某同学使用计算器求 30 个数据的平均数时，错将其中一个数 据 105 输入为 15，则由此求出的平均数与实际平均数的差是( ) A．3.5 B．－3 C.3 D．－0.5 【解析】 少输入 90，90 30 ＝3，平均数少 3，求出的平均数减去实 际平均数等于－3. 【答案】 B 4．某校现有高一学生 210 人，高二学生 270 人，高三学生 300 人， 学校学生会用分层抽样的方法从这三个年级的学生中抽取 n 个学生进 行问卷调查，如果已知从高一学生中抽取的人数为 7 人，那么从高三 学生中抽取的人数应为( ) A．10 B．9 C.8 D．7 【解析】 由题意知抽取的比例为 7 210 ＝ 1 30 ， 故从高三中抽取的人数为 300× 1 30 ＝10. 【答案】 A 5．一个容量为 100 的样本，其数据的分组与各组的频数如下： 组别 [0，10) [10，20) [20，30) [30，40) [40，50) [50，60) [60，70] 频数 12 13 24 15 16 13 7 则样本数据在[10，40)上的频率为( ) A．0.13 B．0.39 C.0.52 D．0.64 【解析】 频率为13＋24＋15 100 ＝0.52. 【答案】 C 6．如图 2 是一容量为 100 的样本的质量的频率分布直方图，则由 图可估计样本质量的中位数为( ) 图 2 A．11 B．11.5 C.12 D．12.5 【解析】 由频率分布直方图得组距为 5，故样本质量在[5，10)， [10，15)内的频率分别为 0.3 和 0.5，从而中位数为 10＋0.2 0.5 ×5＝12， 故选 C. 【答案】 C 7．高三某班有学生 56 人，现将所有同学随机编号，用系统抽样 的方法，抽取一个容量为 4 的样本，已知 5 号、33 号、47 号学生在样 本中，则样本中还有一个学生的编号为( ) A．13 B．17 C.19 D．21 【解析】 因为 47－33＝14，所以由系统抽样的定义可知样本中 的另一个学生的编号为 5＋14＝19. 【答案】 C 8．在某次测量中得到的 A 样本数据如下：52，54，54，56，56， 56，55，55，55，55.若 B 样本数据恰好是 A 样本数据都加 6 后所得数 据，则 A，B 两样本的下列数字特征对应相同的是( ) A．众数 B．平均数 C．中位数 D．标准差 【解析】 由题意可知 B 样本的数据为 58，60，60，62，62，62， 61，61，61，61，将 A 样本中的数据由小到大依次排列为 52，54，54， 55，55，55，55，56，56，56，将 B 样本中的数据由小到大依次排列 为 58，60，60，61，61，61，61，62，62，62，因此 A 样本的众数为 55，B 样本的众数为 61，A 选项错误；A 样本的平均数为 54.8，B 样本 的平均数为 60.8，B 选项错误；A 样本的中位数为 55，B 样本的中位 数为 61，C 选项错误；事实上，在 A 样本的每个数据上加上 6 后形成 B 样本，样本的稳定性不变，因此两个样本的标准差相等，故选 D. 【答案】 D 9．如图 3 茎叶图记录了甲、乙两组各五名学生在一次英语听力测 试中的成绩．(单位：分) 图 3 已知甲组数据的平均数为 17，乙组数据的中位数为 17，则 x，y 的值分别为( ) A．2，6 B．2，7 C．3，6 D．5，7 【解析】 依题意得 9＋10×2＋2＋x＋20×2＋7＋4＝17×5，即 x＝5；y＝7，故选 D. 【答案】 D 10．在样本频率分布直方图中，共有 11 个小长方形，若中间一个 小长方形的面积等于其他 10 个小长方形面积和的1 4 ，且样本容量为 160，则中间一组的频数为( ) A．32 B．0.2 C.40 D．0.25 【解析】 由频率分布直方图的性质，可设中间一组的频率为 x， 则 x＋4x＝1， 所以 x＝0.2，故中间一组的频数为 160×0.2＝32，选 A. 【答案】 A 11．如图 4 所示，样本 A 和 B 分别取自两个不同的总体，它们的 样本平均数分别为 x－ A 和 x－ B，样本标准差分别为 sA 和 sB，则( ) 图 4 A． x－ A＞ x－ B，sA＞sB B． x－ A＜ x－ B，sA＞sB C． x－ A＞ x－ B，sA＜sB D． x－ A＜ x－ B，sA＜sB 【解析】 A 中的数据都不大于 B 中的数据，所以 x－ A＜ x－ B，但 A 中的数据比 B 中的数据波动幅度大，所以 sA＞sB. 【答案】 B 12．(2014·陕西高考)某公司 10 位员工的月工资(单位：元)为 x1， x2，…，x10，其均值和方差分别为 x－和 s2，若从下月起每位员工的月工 资增加 100 元，则这 10 位员工下月工资的均值和方差分别为( ) A. x－，s2＋1002 B． x－＋100，s2＋1002 C. x－，s2 D． x－＋100，s2 【解析】 x1＋x2＋…＋x10 10 ＝ x－，yi＝xi＋100，所以 y1，y2，…， y10 的均值为 x－＋100，方差不变，故选 D. 【答案】 D 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分，把答案填在 题中横线上)． 13．(2014·天津高考)某大学为了解在校本科生对参加某项社会实 践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中 抽取一个容量为 300 的样本进行调查，已知该校一年级、二年级、三 年级、四年级的本科生人数之比为 4∶5∶5∶6，则应从一年级本科生 中抽取________名学生． 【解析】 根据题意，应从一年级本科生中抽取的人数为 4 4＋5＋5＋6 ×300＝60. 【答案】 60 14．某地区对某路段公路上行驶的汽车速度实施监控，从中抽取 50 辆汽车进行测试分析，得到如图 5 所示的时速的频率分布直方图， 根据下图，时速在 70 km/h 以下的汽车有________辆． 图 5 【解析】 由频率分布直方图可得时速在 70 km/h 以下的频率是 (0.01＋0.03)×10＝0.4，所以频数是 0.4×50＝20. 【答案】 20 15．一个车间为了规定工时定额，需要确定加工零件所花费的时 间，为此进行了 5 次试验，收集数据如下： 零件数 x(个) 10 20 30 40 50 加工时间 y(分钟) 64 69 75 82 90 由表中数据，求得线性回归方程为y^＝0.65x＋a^，根据回归方程， 预测加工 70 个零件所花费的时间为________分钟． 【解析】 由数据可得 x－＝30， y－＝76，将中心点(30，76)代入线 性回归方程可得a^＝76－0.65×30＝56.5，所以线性回归方程为y^＝0.65x ＋56.5.当 x＝70 时，y^＝0.65×70＋56.5＝102. 【答案】 102 16．从某小学随机抽取 100 名同学，将他们的身高(单位：厘米) 数据绘制成频率分布直方图(如图 6)．由图中数据可知 a＝________．若 要从身高在[120，130)，[130，140)，[140，150]三组的学生中，用分 层抽样的方法选取 18 人参加一项活动，则从身高在[140，150]的学生 中选取的人数应为________. 【导学号：28750046】 图 6 【 解 析 】 ∵0.005×10 ＋ 0.035×10 ＋ a×10 ＋ 0.020×10 ＋ 0.010×10＝1， ∴a＝0.030. 设身高在[120，130)，[130，140)，[140，150]三组的学生分别有 x， y，z 人， 则 x 100 ＝0.030×10，解得 x＝30. 同理，y＝20，z＝10. 故从[140，150]的学生中选取的人数为 10 30＋20＋10 ×18＝3. 【答案】 0.030 3 三、解答题(本大题共 6 小题，共 70 分，解答应写出文字说明，证 明过程或演算步骤) 17．(本小题满分 10 分)一批产品中，有一级品 100 个，二级品 60 个，三级品 40 个，分别用系统抽样和分层抽样的方法，从这批产品中 抽取一个容量为 20 的样本． 【解】 (1)系统抽样的方法： 先将 200 个产品随机编号：001，002，…，200，再将 200 个产品 按 001～010，011～020，…，191～200，分成 20 组，每组 10 个产品， 在第一组内用简单随机抽样确定起始的个体编号，按事先确定的规则， 从每组中分别抽取样本，这样就得到一个容量为 20 的样本． (2)分层抽样的方法： 先将总体按其级别分为三层，一级品有 100 个，产品按 00，01，…， 99 编号；二级品有 60 个，产品按 00，01，…，59 编号；三级品有 40 个，产品按 00，01，…，39 编号．因总体个数：样本容量为 10∶1， 故用简单随机抽样的方法：在一级品中抽 10 个，二级品中抽 6 个，三 级品中抽 4 个．这样就得到一个容量为 20 的样本． 18．(本小题满分 12 分)某公司为了了解一年内的用水情况，抽取 了 10 天的用水量如下表所示： 天数 1 1 1 2 2 1 2 用水量/吨 22 38 40 41 44 50 95 (1)在这 10 天中，该公司用水量的平均数是多少？ (2)在这 10 天中，该公司每天用水量的中位数是多少？ (3)你认为应该用平均数和中位数中的哪一个数来描述该公司每天 的用水量？ 【解】 (1) x－＝ 1 10(22＋38＋40＋2×41＋2×44＋50＋2×95)＝ 51(吨)． (2)中位数为41＋44 2 ＝42.5(吨)． (3)平均数受数据中的极端值(2 个 95)影响较大，使平均数在估计总 体时可靠性降低，10 天的用水量有 8 天都在平均值以下，故用中位数 描述每天的用水量更合适． 19．(本小题满分 12 分)两台机床同时生产一种零件，在 10 天中， 两台机床每天的次品数如下： 甲：1，0，2，0，2，3，0，4，1，2. 乙：1，3，2，1，0，2，1，1，0，1. (1)哪台机床次品数的平均数较小？ (2)哪台机床的生产状况比较稳定？ 【解】 (1) x－ 甲＝(1＋0＋2＋0＋2＋3＋0＋4＋1＋2)× 1 10 ＝1.5， x－ 乙＝(1＋3＋2＋1＋0＋2＋1＋1＋0＋1)× 1 10 ＝1.2. ∵ x－ 甲> x－ 乙， ∴乙车床次品数的平均数较小． (2)s2甲＝ 1 10[(1－1.5)2＋(0－1.5)2＋(2－1.5)2＋(0－1.5)2＋(2－1.5)2＋ (3－1.5)2＋(0－1.5)2＋(4－1.5)2＋(1－1.5)2＋(2－1.5)2]＝1.65， 同理 s2乙＝0.76，∵s2甲>s2乙， ∴乙车床的生产状况比较稳定． 20．(本小题满分 12 分)农科院的专家为了了解新培育的甲、乙两 种麦苗的长势情况，从甲、乙两种麦苗的试验田中各抽取 6 株麦苗测 量麦苗的株高，数据如下：(单位：cm) 甲：9，10，11，12，10，20 乙：8，14，13，10，12，21. 图 7 (1)在如图 7 给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎 叶图； (2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差，并由 此判断甲、乙两种麦苗的长势情况． 【解】 (1)茎叶图如图所示： (2) x－ 甲＝9＋10＋11＋12＋10＋20 6 ＝12， x－ 乙＝8＋14＋13＋10＋12＋21 6 ＝13， s2甲≈13.67，s2乙≈16.67. 因为 x－ 甲＜ x－ 乙，所以乙种麦苗平均株高较高，又因为 s2甲＜s2乙，所 以甲种麦苗长得较为整齐． 21．(本小题满分 12 分)某医院用光电比色计检验尿汞时，得尿汞 含量(mg/L)与消光系数如下表： 尿汞含量 x 2 4 6 8 10 消光系数 y 64 134 205 285 360 (1)如果 y 与 x 之间具有线性相关关系，求回归直线方程； (2)估计尿汞含量为 9 mg/L 时的消光系数． 【解】 (1)设回归直线方程为y^＝b^x＋a^. ∵ x－＝6， y－＝209.6， ∴b^＝7 774－5×6×209.6 220－5×62 ＝1 486 40 ＝37.15. ∴a^＝209.6－37.15×6＝－13.3. ∴回归方程为y^＝37.15x－13.3. (2)∵当 x＝9 时，y^＝37.15×9－13.3≈321， ∴估计尿汞含量为 9 mg/L 时消光系数为 321. 22．(本小题满分 12 分)某班 100 名学生期中考试语文成绩的频率 分布直方图如图 8 所示，其中成绩分组区间是：[50，60)，[60，70)， [70，80)，[80，90)，[90，100]． 图 8 (1)求图中 a 的值； (2)根据频率分布直方图，估计这 100 名学生语文成绩的平均分； (3)若这 100 名学生语文成绩某些分数段的人数(x)与数学成绩相应 分数段的人数(y)之比如下表所示，求数学成绩在[50，90)之外的人数. 分数段 [50，60) [60，70) [70，80) [80，90) x∶y 1∶1 2∶1 3∶4 4∶5 【解】 (1)由频率分布直方图知(2a＋0.02＋0.03＋0.04)×10＝1， 解得 a＝0.005. (2)由频率分布直方图知这 100 名学生语文成绩的平均分为 55×0.005×10 ＋ 65×0.04×10 ＋ 75×0.03×10 ＋ 85×0.02×10 ＋ 95×0.005×10＝73(分)． (3)由频率分布直方图知语文成绩在[50，60)，[60，70)，[70，80)， [80，90)各分数段的人数依次为 0.005×10×100＝5；0.04×10×100＝ 40；0.03×10×100＝30；0.02×10×100＝20. 由题中给出的比例关系知数学成绩在上述各分数段的人数依次为 5；40×1 2 ＝20；30×4 3 ＝40；20×5 4 ＝25. 故数学成绩在[50，90)之外的人数为 100－(5＋20＋40＋25)＝10.