高考数学专题复习教案： 复数加、减法的几何意义 2页

复数加、减法的几何意义 主标题：复数加、减法的几何意义 副标题：为学生详细的分析复数加、减法的几何意义的高考考点、命题方向以及规律总结。‎ 关键词：复数加法，减法，几何意义，知识总结 难度：3‎ 重要程度：5‎ 考点剖析：本考点包括复数加、减法的几何意义，复数和复平面的关系，利用数形结合解决有关问题。‎ 命题方向：‎ ‎1.利用复数与复平面内的点是一一对应关系，利用点所在的象限解题是近几年高考的热点．‎ ‎2.复数与从原点出发的向量是一一对应的关系，根据向量的几何意义，利用复数加法和减法的几何意义解题．‎ ‎3.题型以选择题和填空题为主，属于基础题.‎ 规律总结：‎ ‎1. 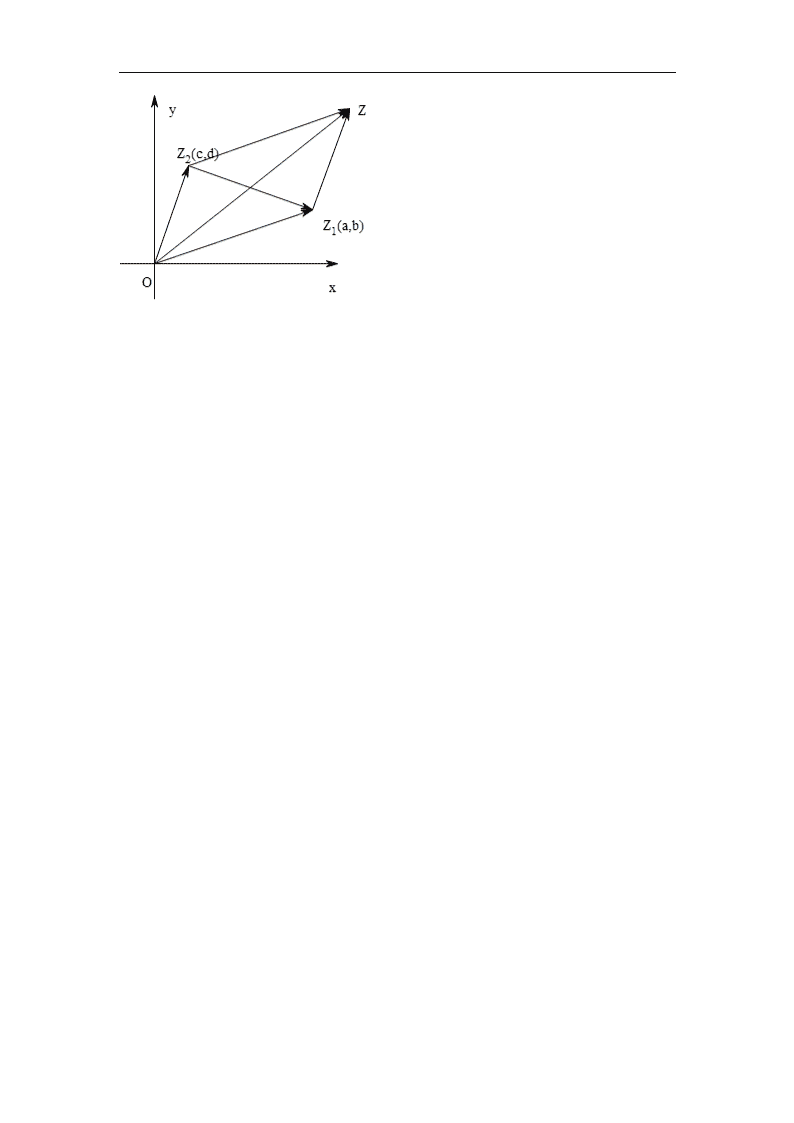复数加、减法的几何意义规律总结 一个平面 建立了直角坐标系表示来表示复数的平面叫做复平面.‎ 两个对应 ‎(1)复数z＝a＋bi(a，b∈R)与复平面内的点Z(a，b)是一一对应的关系．‎ ‎(2)换复数z＝a＋bi(a，b∈R)与平面向量是一一对应的关系．‎ 两个法则 复数加法的几何意义：复数的加法满足平行四边形法则或三角形法则；‎ 复数减法的几何意义：复数减法满足三角形法则.‎ 知识归纳 复平面：建立了直角坐标系来表示复数的平面叫做复平面，x轴叫做实轴，y轴叫做虚轴.‎ ‎ 实轴上的点都表示实数，除原点外，虚轴上的点表示纯虚数.‎ 复数的模：复数所对应的向量的模即为复数的模.‎ ‎ 复数z＝a＋bi(a，b∈R)的模表示为.‎ 复数加法的几何意义：设，(a，b，c，d∈R)，则可以表示为.‎ 复数减法的几何意义：设，(a，b，c，d∈R)，则可以表示为.‎ ‎ ‎ ‎ ‎