高中数学必修2教案：1_1_2简单组合体的结构特征 3页

第二课时 简单组合体的结构特征 ‎（一）教学目标 ‎1．知识与技能 ‎（1）理解由柱、锥、台、球组成的简单组合体的结构特征.‎ ‎（2）能运用简单组合体的结构特征描述现实生活中的实际模型.‎ ‎2．过程与方法 让学生通过下观感觉空间物体，认识简单的组合体的结构特征，归纳简单组合体的基本构成形式.‎ ‎3．情感态度与价值观 培养学生的空间想象能力，培养学习教学应用意识.‎ ‎（二）重点、难点 重点与难点都是认识简单组体体的结构特征.‎ ‎（三）教学方法 概念形成过程中，学生观察、思考、讨论、交流与教师引导相结合，然后通过对一些具体问题的讨论，加深对简单组合体的结构特征的理解.‎ 教学环节 教学内容 师生互动 设计意图 创设情境 观察教材下列各图，说出这些几何体是由哪些简单几何体构成的.‎ ‎ ‎ 学生回答，然后师生共同讨论他们的联系与区别.‎ 通过问题解决，学生复习了上课时所学知识，同学又为学习新知识作准备 概念形成 ‎1．简单组合体概念，由柱体锥体，台体和球体等简单几何体组合而成的几何体.‎ 学生归纳，总结后教师予以适当修饰，补充.‎ 培养学生总结概括，表述的能力，加强对概念的理解.‎ ‎2．简单组合体为构成有两种基本形式：一种是由简单几何体拼接而成，一种是由简单几何体截去或挖去一部分而成.‎ 应用举例 例1 已知球的外切圆台上、下底面的半径分别为r，R，求球的半径.‎ ‎【解析】圆台轴截面为等腰梯形，与球的大圆相切，由此得梯形腰长为R + r，梯形的高即球的直径为=2，所以，球的半径为.‎ 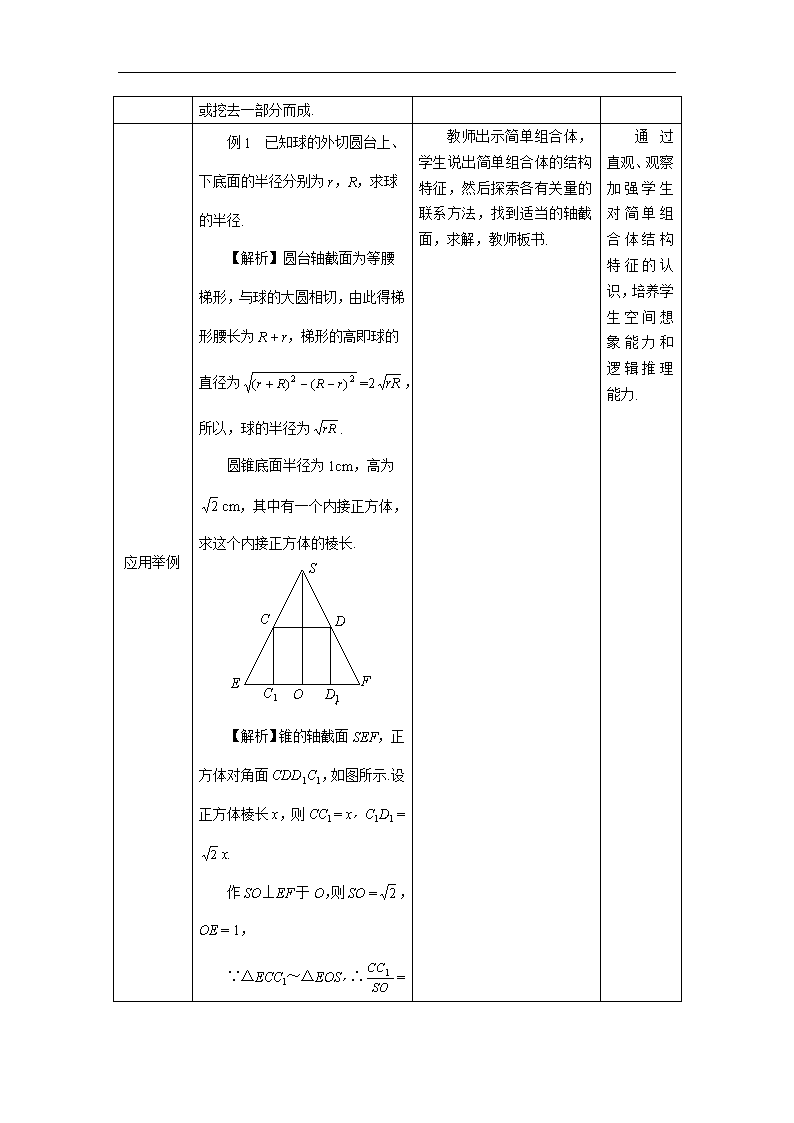圆锥底面半径为1cm，高为cm，其中有一个内接正方体，求这个内接正方体的棱长.‎ E C1‎ O D1=1‎ F D C S ‎【解析】锥的轴截面SEF，正方体对角面CDD1C1，如图所示.设正方体棱长x，则CC1 = x，C1D1 =x.‎ 作SO⊥EF于O，则SO =，OE = 1，‎ ‎∵△ECC1～△EOS，∴=‎ 教师出示简单组合体，学生说出简单组合体的结构特征，然后探索各有关量的联系方法，找到适当的轴截面，求解，教师板书.‎ 通过直观、观察加强学生对简单组合体结构特征的认识，培养学生空间想象能力和逻辑推理能力.‎ ‎，即=.‎ ‎∴x=（cm），即内接正方体棱长为cm.‎ 归纳总结 一、知识点 ‎（1）简单组合体定义 ‎（2）简单组合体构成形式 二、注意事项 轴截面在旋转体与多面体组合而成的几何体中的应用.‎ 师生共同总结——交流——完善 巩固、加深对概念的理解、培养思维严谨性.‎ 课后作业 ‎1.1 第二课时 习案 学生独立完成 巩固深化，提高学生解决问题的能力.‎ 备选例题 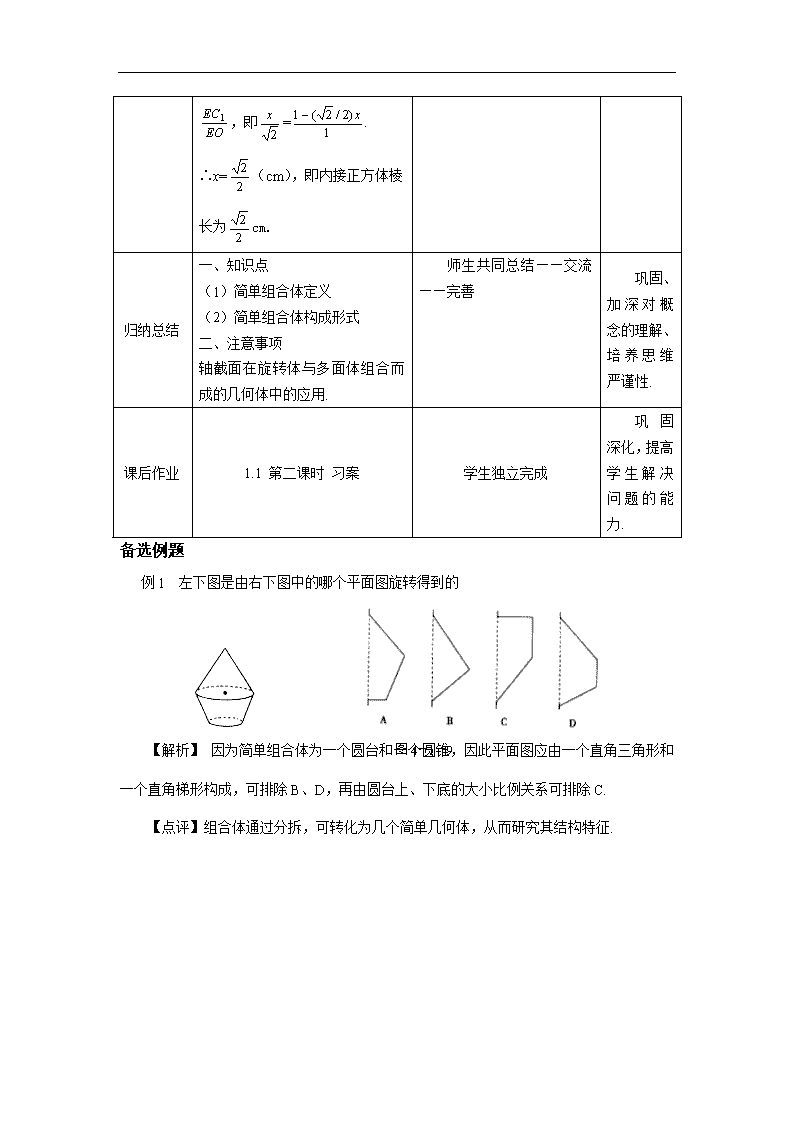例1 左下图是由右下图中的哪个平面图旋转得到的 图4—1—9‎ ‎ ‎ ‎ 【解析】 因为简单组合体为一个圆台和一个圆锥，因此平面图应由一个直角三角形和一个直角梯形构成，可排除B、D，再由圆台上、下底的大小比例关系可排除C. ‎ ‎ 【点评】组合体通过分拆，可转化为几个简单几何体，从而研究其结构特征. ‎