2020学年高二数学下学期期末考试试题 文（新版）新人教版(1) 10页

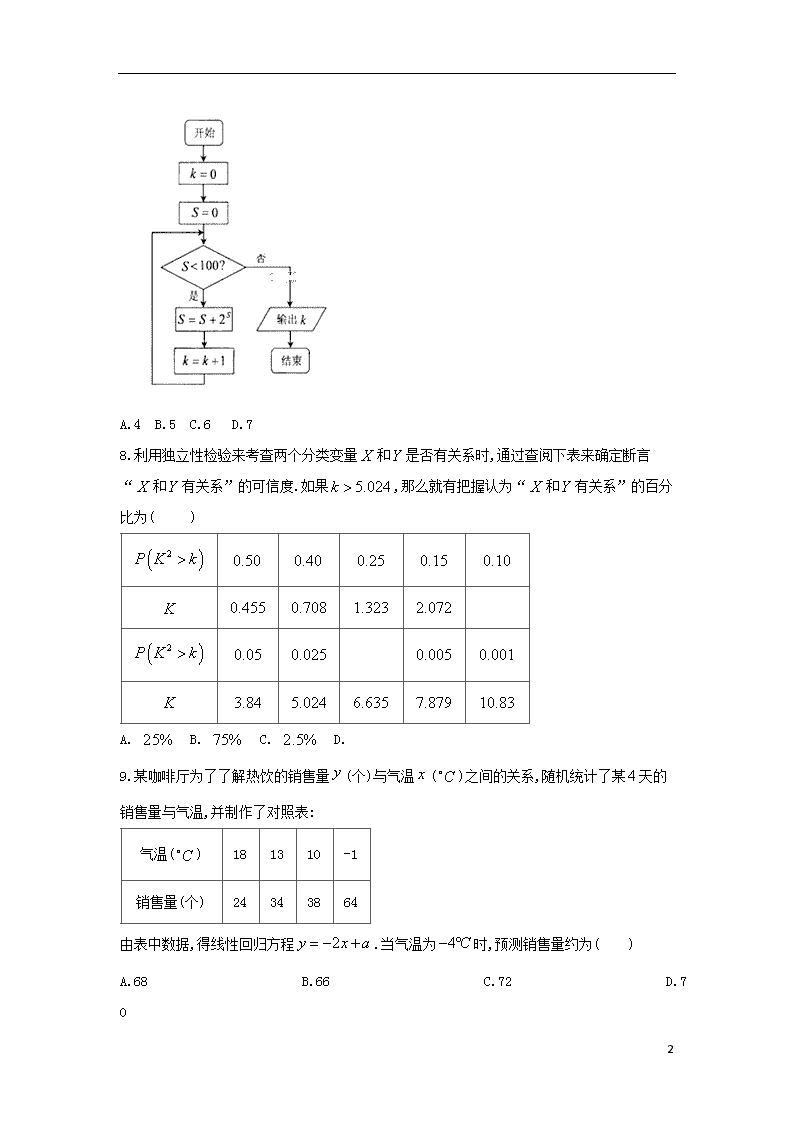
‎2019学年高二数学下学期期末考试试题 文 一、选择题 ‎1.直线l的参数方程为 (为参数),则直线与坐标轴的交点分别为(    )‎ A. B. C. D. ‎ ‎2.圆的圆心坐标是(   )‎ A.(0,2)      B.(2,0)      C.(0,-2)     D.(-2,0)‎ ‎3.已知圆:在伸缩变换的作用下变成曲线,则曲线的方程为(   )‎ A. B. C. D. ‎ ‎4.在极坐标系中,过点并且与极轴垂直的直线方程是(   )‎ A. B. C. D. ‎ ‎5.复数的共轭复数是( )‎ A. B. C. D. ‎ ‎6.复数的模为(   )‎ A. B. C. D. ‎ ‎7某程序框图如图所示,该程序运行后输出的的值是(    )‎ 10‎ A.4 B.5 C.6 D.7‎ ‎8.利用独立性检验来考查两个分类变量和是否有关系时,通过查阅下表来确定断言“和有关系”的可信度.如果,那么就有把握认为“和有关系”的百分比为(   )‎ A. B. C. D. ‎ ‎9.某咖啡厅为了了解热饮的销售量(个)与气温()之间的关系,随机统计了某天的销售量与气温,并制作了对照表:‎ 气温()‎ ‎18‎ ‎13‎ ‎10‎ ‎-1‎ 销售量(个)‎ ‎24‎ ‎34‎ ‎38‎ ‎64‎ 由表中数据,得线性回归方程.当气温为时,预测销售量约为(   )‎ A.68           B.66           C.72           D.70‎ 10‎ ‎10.函数的单调减区间为(   )‎ A., B., C. D.,‎ ‎11.设是函数的导函数, 的图象如下图所示, 则的图象最有可能的是(   ) ‎ ‎12.曲线在点处的切线的倾斜角为( ).‎ A.30°       B.45°       C.60°       D.120°‎ 二、填空题 ‎13.春节期间,某销售公司每天销售某种取暖商品的销售额 (单位:万元)与当天的平均气温 (单位:℃)有关.现收集了春节期间这个销售公司天的与的数据列于下表:‎ 平均气温(℃)‎ 销售额(万元)‎ 根据以上数据,求得与之间的线性回归方程的系数,则 __________‎ ‎14.已知函数,则函数的单调减区间为_________.‎ ‎15.在极坐标系中,点到圆的圆心的距离为__________‎ ‎16.在极坐标系中,曲线与的交点的极坐标为__________.‎ 10‎ 三、解答题 ‎17.已知复数,, 且为纯虚数,求复数.‎ ‎18.已知曲线的极坐标方程,曲线的极坐标方程为,曲线,相交于两点.‎ ‎1.把曲线,的极坐标方程化为直角方程;‎ ‎2.求弦的长度.‎ ‎19.已知满足,求的最值.‎ ‎20.某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于分为优秀, 分以下为非优秀.统计成绩后,得到如下的列联表,且已知在甲、乙两个文科班全部人中随机抽取人为优秀的概率为.‎ 优秀 非优秀 合计 甲班 乙班 合计 ‎1.请完成上面的列联表; 2.根据列联表的数据,若按的可靠性要求,能否认为“成绩与班级有关系”; 3.若按下面的方法从甲班优秀的学生中抽取一人;把甲班优秀的名学生从到进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到号或号的概率. 参考公式与临界值表: .‎ 10‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎21.从某居民区随机抽取个家庭,获得第个家庭的月收入 (单位:千元)与月储蓄 (单位:千元)的数据资料,算得,,,. 1.求家庭的月储蓄对月收入的线性回归方程; 2.判断变量与之间是正相关还是负相关;‎ ‎3.若该居民区某家庭月收入为千元,预测该家庭的月储蓄. 其中,为样本平均值,线性回归方程也可写为,‎ 附:线性回归方程中, ,.‎ ‎22.已知函数在点处取得极值. 1.求的值; 2.若有极大值28,求在上的最小值.‎ 10‎ 参考答案 ‎ ‎ 一、选择题 ‎1.答案：B 解析：本题主要考查直线的参数方程.当时, ,故直线与轴的交点为;当时, ,故直线与轴的交点为.‎ ‎2.答案：A 解析：本题考查参数方程与普通方程的互化.消去参数,得圆的方程为,所以圆心坐标为.‎ ‎3.答案：A 解析：由题意得代入圆的方程得,即双曲线的方程为.‎ ‎4.答案：C 解析：在直角坐标系中,过点并且与极轴垂直的直线方程是, 其极坐标方程为 , 故选 C. ‎ ‎5.答案：D 解析：,‎ 所以复数共轭复数是.‎ ‎6.答案：B 10‎ 解析：由得,∴,故选B.‎ 答案： A 解析： 当,时,运行程序可得,,‎ 继续运行得,,‎ 继续运行得,,‎ 继续运行得,,,‎ 结束循环,输出.‎ ‎8.答案：D ‎9.答案：A 解析：由题,‎ ‎,‎ 所以 即线性回归方程为 ,‎ 当时,‎ ‎10.答案：A ‎11.答案：C 解析：由的图象易得当或时, , 故函数在区间和上单调递增; 当时, ,故函数在区间上单调递减; 故选C.‎ ‎12.答案：B 解析：,∴,∴倾斜角为45°.‎ 二、填空题 ‎13.答案：‎ 10‎ ‎14.答案：‎ 解析：由得其导数为,令,得.‎ ‎15.答案：‎ ‎16.答案：‎ 由,得,其直角坐标方程为的直角坐标方程为,由解得则,故点的极坐标为.‎ 三、解答题 ‎17.答案：,因为是纯虚数,所以且,解得,故.‎ ‎18.答案：1. 由,得,所以,即曲线的在极坐标方程为.‎ 由,可知曲线的在极坐标方程为. 2.因为圆心到直线的距离,‎ 所以弦长,所以的长度为.‎ ‎19.答案：由可知,曲线表示以为圆心,以2为半径的圆,令, (为参数),则 (其 10‎ 中). ∵, ∴当时,S有最大值, ; 当时,S有最小值, . ∴S的最大值为;S的最小值为. ‎ ‎20.答案：1.‎ 优秀 非优秀 合计 甲班 ‎ ‎ ‎  ‎ ‎ ‎ 乙班 ‎  ‎ ‎ ‎ 合计 ‎  ‎ ‎ 2.根据列联表中的数据,得到. 因此按的可靠性要求,不能认为“成绩与班级有关系”. 3.设“抽到或号”为事件,先后两次抛掷一枚均匀的骰子,出现的点数为 所有的基本事件有共个. 事件包含的基本事件有共个. ∴,即抽到号或号的概率为.‎ ‎21.答案：1.由题意知, ,, , ‎ 10‎ ‎, 由此可得,, 故所求线性回归方程为. 2.由于变量的值随值的增加而增加,故与之间是正相关. 3.将代入回归方程可以预测该家庭的月储蓄为 (千元).‎ ‎22.答案：1.由题,可得, 又函数在点处取得极值 ∴,即, 化简得解得,. 2.由第一问知,, 令, 解得, 当时, ,故在上为增函数; 当时, ,故在上为减函数; 当时, ,故在上为增函数; 由此可知在处取得极大值,在处取得极小值, 由题设条件知得, 此时,, 因此在上的最小值.‎ 10‎