海淀区2016届高三一模数学（理）试题及答案 15页

海淀区高三年级第二学期期中练习 数学（理科） 2016.4‎ 本试卷共4页，150分。考试时长120分钟。考生务必将答案答在答题卡上，在试卷上 作答无效。考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。‎ ‎1. 函数的定义域为 ‎ ‎ A. B. C. D.‎ ‎2. 某程序的框图如图所示，若输入的（其中为虚数单位），则输出 ‎ ‎ 的值为 ‎ A. B. C. D. ‎ ‎3. 若满足 则的最大值为 ‎ ‎ A. B. C. D.‎ ‎4. 某三棱椎的三视图如图所示，则其体积为 ‎ ‎ A. B. C. D. ‎ ‎5. 已知数列的前项和为，则“为常数列”是“，”的 ‎ A. 充分不必要条件 B. 必要不充分条件 ‎ C. 充分必要条件 D. 既不充分也不必要条件 ‎6. 在极坐标系中，圆与圆相交于两点， 则 ‎ ‎ A. B. C. D.2‎ ‎7. 已知函数 是偶函数，则下列结论可能成立的是 ‎ ‎ A. B. ‎ ‎ C. D. ‎ 一 二 三 四 五 甲 ‎15‎ ‎17‎ ‎14‎ ‎17‎ ‎15‎ 乙 ‎22‎ ‎23‎ ‎21‎ ‎20‎ ‎20‎ 丙 ‎9‎ ‎13‎ ‎14‎ ‎12‎ ‎10‎ 丁 ‎7‎ ‎9‎ ‎11‎ ‎9‎ ‎11‎ 戊 ‎13‎ ‎15‎ ‎14‎ ‎15‎ ‎11‎ ‎8. 某生产基地有五台机器设备，现有五项工作待完成，每台机器完成每项工作获得的效益值如右表所示. 若每台机器只完成一项工作，且完成五项工作后获得的效益值总和最大，则下列描述正确的是 ‎ ‎ A. 甲只能承担第四项工作 ‎ B. 乙不能承担第二项工作 ‎ C. 丙可以不承担第三项工作 ‎ D. 丁可以承担第三项工作 二、填空题共6小题，每小题5分，共30分。‎ ‎9. 已知向量 若，则 ‎ ‎10. 在等比数列中，，且，则的值为___. ‎ ‎11. 在三个数中，最小的数是__. ‎ ‎12. 已知双曲线的一条渐近线的倾斜角为，则的离心率为__;‎ 若的一个焦点到 的距离为,则的方程为__. ‎ ‎13. 如图,在 在三角形三条边上的个不同的圆内填上数字其中的一个.‎ ‎(i) 当每条边上的三个数字之和为4时，不同的填法有___种；‎ ‎ (ii) 当同一条边上的三个数字都不同时，不同的填法有__种. ‎ ‎14. 已知函数，对于给定的实数，若存在，满足：，使得 ‎ ‎ ，则记的最大值为. ‎ ‎ （i） 当时，___；‎ ‎ （ii）当且时，函数的值域为___.‎ 三、解答题共6小题，共80分。解答应写出文字说明、演算步骤或证明过程。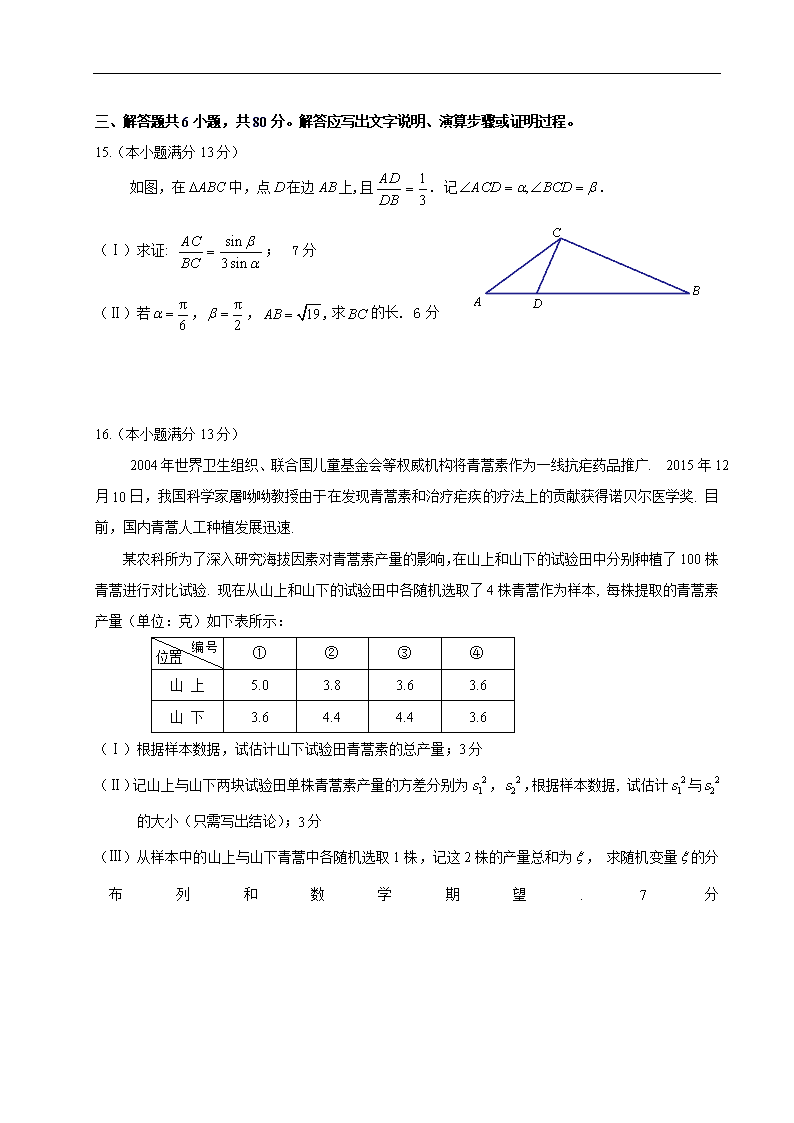‎ ‎15.（本小题满分13分）‎ ‎ 如图，在中，点在边上,且. 记.‎ ‎（Ⅰ）求证: ； 7分 ‎（Ⅱ）若，，,求的长. 6分 ‎16.（本小题满分13分）‎ ‎ 2004年世界卫生组织、联合国儿童基金会等权威机构将青蒿素作为一线抗疟药品推广. ‎2015年12月10日，我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖. 目前，国内青蒿人工种植发展迅速. ‎ 某农科所为了深入研究海拔因素对青蒿素产量的影响，在山上和山下的试验田中分别种植了100株青蒿进行对比试验. 现在从山上和山下的试验田中各随机选取了4株青蒿作为样本, 每株提取的青蒿素产量（单位：克）如下表所示：‎ ‎①‎ ‎②‎ ‎③‎ ‎④‎ 山 上 ‎5.0‎ ‎3.8‎ ‎3.6‎ ‎3.6‎ 山 下 ‎3.6‎ ‎4.4‎ ‎4.4‎ ‎3.6‎ ‎（Ⅰ）根据样本数据，试估计山下试验田青蒿素的总产量；3分 ‎（Ⅱ）记山上与山下两块试验田单株青蒿素产量的方差分别为，，根据样本数据, 试估计与 ‎ ‎ 的大小（只需写出结论）；3分 ‎（Ⅲ）从样本中的山上与山下青蒿中各随机选取1株，记这2株的产量总和为， 求随机变量的分布列和数学期望. 7分 ‎17.（本小题满分14分）‎ 如图，在四棱锥中，平面，四边形为正方形，点分别为线段上的点，. ‎ ‎（Ⅰ）求证：平面； 4分 ‎（Ⅱ）求证：当点不与点重合时，四个点在同一个平 ‎ 面内；5分 ‎（Ⅲ）当，二面角大小为为时，求的长. ‎ ‎ 5分 ‎18.（本小题满分13分）‎ 已知函数，. ‎ ‎（Ⅰ）求函数的最小值； ‎ ‎（Ⅱ）求函数的单调区间；‎ ‎(Ⅲ) 求证：直线不是曲线的切线.‎ ‎19.（本小题满分14分）‎ ‎　　 已知椭圆的离心率为，椭圆与轴交于两点，. ‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设点是椭圆上的一个动点，且点在轴的右侧. 直线，与直线分别相交于 两点. 若以为直径的圆与轴交于两点，求点横坐标的取值范围及的最大值. ‎ ‎20.（本小题满分13分）‎ ‎ 给定正整数，集合. 若存在集合，同时满足下列三个条件：　‎ ‎①, ; ‎ ‎②集合中的元素都为奇数，集合中的元素都为偶数，所有能被3整除的数都在集合中 ‎ （集合中还可以包含其它数）；‎ ‎ ③集合中各元素之和分别为，有; ‎ ‎ 则称集合为可分集合.‎ ‎（I） 已知为可分集合，写出相应的一组满足条件的集合；‎ ‎（II）证明：若是3的倍数，则不是可分集合；‎ ‎（III）若为可分集合且为奇数，求的最小值．‎ 海淀区高三年级第二学期期中练习参考答案 数学（理科） 2016.4 ‎ 阅卷须知:‎ ‎1.评分参考中所注分数，表示考生正确做到此步应得的累加分数。‎ ‎2.其它正确解法可以参照评分标准按相应步骤给分。‎ 一、选择题（本大题共8小题,每小题5分,共40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A D C A C B C B 二、填空题（本大题共6小题,每小题5分, 有两空的小题，第一空3分，第二空2分，‎ 共30分）‎ ‎9． ‎ ‎ 10． ‎ ‎ 11. ‎ ‎12．‎ ‎ 13． ‎ ‎ 14． ‎ 三、解答题(本大题共6小题,共80分)‎ ‎15．解：（Ⅰ） ‎ 在中，由正弦定理,有 …………………2分 在中，由正弦定理,有 …………………4分 因为,所以 …………………6分 因为, 所以 …………………7分 ‎（Ⅱ）因为，,‎ 由（Ⅰ）得 …………………9分 设,由余弦定理,‎ ‎ …………………11分 代入,得到, ‎ 解得,所以. …………………13分 ‎16解: (I)由山下试验田4株青蒿样本青蒿素产量数据，得样本平均数 ‎ …………………2分 ‎ 则山下试验田株青蒿的青蒿素产量估算为 ‎ g …………………3分 ‎（Ⅱ）比较山上、山下单株青蒿素青蒿素产量方差和，结果为.‎ ‎ …………………6分 ‎（Ⅲ）依题意，随机变量可以取， …………………7分 ‎, ‎ ‎, ‎ ‎, …………………9分 ‎7.2‎ ‎7.4‎ ‎8‎ ‎8.2‎ ‎8.6‎ ‎9.4‎ p 随机变量的分布列为 ‎ ‎ ‎ …………………11分 随机变量的期望.‎ ‎ …………………13分 ‎17解: ‎ ‎（Ⅰ）证明：在正方形中，, …………………1分 ‎ 因为平面，平面， 所以. …………………2分 ‎ 因为，且，平面，‎ ‎ 所以平面 …………………4分 ‎（Ⅱ）证明：因为平面，平面, ‎ 所以 …………………5分 在中，，，‎ 所以. …………………6分 在正方形中，, 所以， …………………7分 所以 可以确定一个平面，记为 ‎ 所以四个点在同一个平面内 …………………8分 ‎（Ⅲ）因为平面，平面，‎ ‎ 所以,. ‎ ‎ 又,如图，以为原点，所在直线为轴建立空间直角坐标系, …………………9分 所以.‎ 设平面的一个法向量为，‎ 平面的一个法向量为,‎ 设, ，‎ 因为，所以，‎ 又，所以，即，…………………10分 ‎ 取, 得到, …………………11分 因为，‎ 所以，即， ‎ 取得, 到, …………………12分 因为二面大小为, 所以, ‎ 所以 ‎ 解得, 所以 …………………14分 ‎18解: （Ⅰ）函数的定义域为， …………………1分 ‎ …………………2分 当变化时，，的变化情况如下表：‎ 极小值 ‎ …………………4分 函数在上的极小值为， ‎ 所以的最小值为 …………………5分 ‎（Ⅱ）解：函数的定义域为， …………………6分 ‎ …………………7分 由（Ⅰ）得，，所以 …………………8分 所以的单调增区间是，无单调减区间. …………………9分 ‎（Ⅲ）证明：假设直线是曲线的切线. ………………10分 设切点为，则，即 …………………11分 又，则. …………………12分 所以, 得，与 矛盾 ‎ 所以假设不成立，直线不是曲线的切线 …………………13分 ‎19解：（Ⅰ）由题意可得，， …………………1分 ‎， …………………2分 得， …………………3分 ‎ 解， …………………4分 ‎ 椭圆的标准方程为. …………………5分 ‎（Ⅱ）设，，， ‎ 所以，直线的方程为， …………………6分 同理：直线的方程为， ‎ 直线与直线的交点为， …………………7分 直线与直线的交点为，‎ ‎ 线段的中点， …………………8分 ‎ 所以圆的方程为， …………………9分 令，则， …………………10分 因为，所以 ， …………………11分 所以，‎ 因为这个圆与轴相交,该方程有两个不同的实数解，‎ 所以 ，解得. …………………12分 设交点坐标，则（）‎ 所以该圆被轴截得的弦长为最大值为2. …………………14分 方法二：（Ⅱ）设，，，‎ 所以，直线的方程为， …………………6分 同理：直线的方程为，‎ 直线与直线的交点为， …………………7分 直线与直线的交点为，‎ 若以MN为直径的圆与x轴相交，‎ 则， …………………9分 即 即 …………………10分 因为 ，所以 , …………………11分 ‎ 代入得到 ，解得. …………………12分 该圆的直径为，‎ 圆心到x轴的距离为，‎ 该圆在x轴上截得的弦长为；‎ 所以该圆被轴截得的弦长为最大值为2. …………………14分 ‎ 方法三：‎ ‎（Ⅱ）设，，， ‎ 所以，直线的方程为， …………………6分 同理：直线的方程为，‎ 直线与直线的交点为， …………………7分 直线与直线的交点为，‎ 所以， …………………8分 圆心到x轴的距离为， …………………9分 若该圆与轴相交，则 ， …………………10分 即，‎ 因为 ，所以, …………………11分 所以，解得 …………………12分 该圆在x轴上截得的弦长为；‎ 所以该圆被轴截得的弦长为最大值为2. …………………14分 方法四： 记 , ，设 由已知可得，‎ 所以的直线方程为， ……………………….6分 的直线方程为，‎ 令，分别可得，‎ ‎ ， ……………………….8分 所以 若以为直径的圆与轴相交于，‎ 因为， 所以， ……………………….9分 ‎ ……………………….10分 因为 ，所以, ……………………….11分 代入得到 ‎ 所以， ……………………….12分 所以 ‎ 所以该圆被轴截得的弦长为最大值为2. …………………14分 方法五：‎ 设直线 与交于点 ‎ 因为 轴，所以有 ‎ 所以，所以，所以是的中点. ……………………….6分 又设, 所以直线方程为, ……………………….7分 令,得, 所以 ……………………….8分 ‎ 而 ……………………….9分 若以为直径的圆与轴相交于 则 ……………………….10分 所以 因为 ，所以,代入得到 ……………………….11分 所以，所以或 因为点，所以 ……………………….12分 ‎ 而 ‎ ‎ 所以该圆被轴截得的弦长为最大值为2. …………………14分 ‎20解：‎ ‎（I）依照题意，可以取，， …………………3分 ‎（II）假设存在是的倍数且是可分集合.‎ ‎ 设，则依照题意，‎ 故，‎ 而这个数的和为，故, 矛盾，‎ 所以是3的倍数时，一定不是可分集合 …………………7分 ‎(Ⅲ)35. …………………8分 因为所有元素和为，又中元素是偶数，所以=(为正整数)‎ 所以，因为为连续整数，故这两个数一个为奇数，另一个为偶数 由（Ⅱ）知道，不是3的倍数，所以一定有是的倍数. ‎ 当为奇数时，为偶数，而，‎ 所以一定有既是的倍数，又是的倍数，所以,‎ 所以. …………………10分 定义集合，即集合由集合中所有不是3的倍数的奇数组成，‎ 定义集合，即集合由集合中所有不是3的倍数的偶数组成，‎ 根据集合的性质知道，集合，‎ 此时集合中的元素之和都是，而，‎ 此时中所有的倍数的和为，‎ ‎,‎ 显然必须从集合中各取出一些元素，这些元素的和都是，‎ 所以从集合中必须取偶数个元素放到集合中，所以,‎ 所以，此时 而令集合，‎ 集合，‎ 集合，‎ 检验可知，此时是可分集合, 所以的最小值为. …………………13分