2021版高考数学一轮复习第八章数列8-4数列的求和课件理北师大版 17页

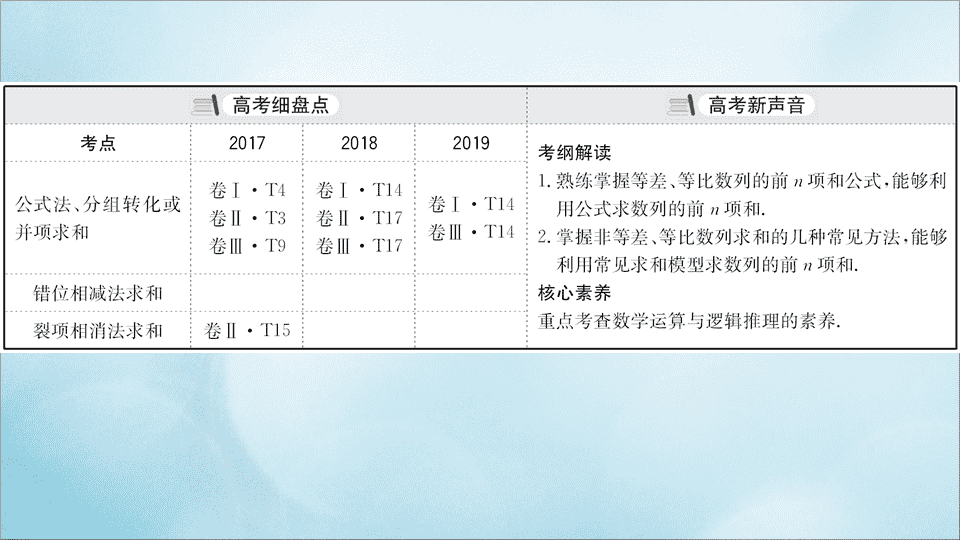
第四节　数列的求和 内容索引 必备知识 · 自主学习 核心考点 · 精准研析 核心素养测评 【教材 · 知识梳理】 1. 等差数列、等比数列求和公式法 (1) 等差数列的前 n 项和公式 S n = = ______________ . (2) 等比数列的前 n 项和公式 S n = 2. 数列求和的几种常用方法 (1) 分组转化法 把数列的每一项分成两项或几项 , 使其转化为几个等差、等比数列 , 再求解 . (2) 裂项相消法 把数列的通项拆成两项之差 , 在求和时中间的一些项可以相互抵消 , 从而求得其和 . 常见的裂项技巧 (3) 错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的 , 这个数列的前 n 项和可用错位相减法求解 . (4) 倒序相加法 如果一个数列 {a n } 的前 n 项中与首末两端等“距离”的两项的和相等或等于同一个常数 , 那么求这个数列的前 n 项和即可用倒序相加法求解 . 3. 几个常用公式 (1)1+2+3+4+…+n=________. (2)1+3+5+7+…+(2n-1)=__. (3)2+4+6+8+…+2n=____. (4)1 2 +2 2 +…+n 2 =_____________. (5)1 3 +2 3 +3 3 +…+n 3 =___________. n 2 n 2 +n 【知识点辨析】 ( 正确的打 “ √ ” , 错误的打 “ × ” ) (1) 如果数列 {a n } 为等比数列 , 且公比不等于 1, 则其前 n 项和为 S n = . ( 　　 ) (2)sin 2 1°+sin 2 2°+sin 2 3°+ … +sin 2 87°+sin 2 88°+sin 2 89° 可用倒序相加求 和 . ( 　　 ) (3) 当 n≥2 时 , ( 　　 ) (4) 求数列 的前 n 项和可用分组求和 .( 　　 ) (5) 求 S n =a+2a 2 +3a 3 +…+na n 时只要把上式等号两边同时乘以 a 即可根据错位相减法求解 . ( 　　 ) 提示 : (1)√. 因为数列 {a n } 为等比数列 , 且公比不等于 1, 则其前 n 项和为 S n = (2)√. 因为 sin 2 1°+sin 2 89°=sin 2 2°+sin 2 88°=sin 2 3°+sin 2 87°=1, 所以 sin 2 1°+sin 2 2°+sin 2 3°+…+sin 2 87°+sin 2 88°+sin 2 89° 可用倒序相加求和 . (3)√. 因为 (4)√. 因为数列 是一个等比数列 与一个等差数列的和数列 , 所以求数列 的前 n 项和可以用分组求和 . (5)×. 要分 a=0 或 a=1 或 a≠0 且 a≠1 讨论求解 . 【易错点索引】 序号 易错警示 典题索引 1 忽视通项的特征 考点一、 T1,3 2 运算错误 考点一、 T4 考点二、典例 3 不能进行合理转化 考点一、 T5 【教材 · 基础自测】 1.( 必修 5P38T4 改编 ) 等差数列 {a n } 中 , 已知公差 d= , 且 a 1 +a 3 + … +a 99 =50, 则 a 2 +a 4 + … +a 100 = ( 　　 ) 　　　　　　　　　　　　　　　　　　 A.50 B.75 C.100 D.125 【解析】 选 B.a 2 +a 4 +…+a 100 =(a 1 +d)+(a 3 +d)+…+(a 99 +d)=(a 1 +a 3 +…+a 99 )+50d= 50+50× =75. 2.( 必修 5P27 例 5(1) 改编 ) 等比数列 {a n } 中 , 若 a 1 =27,a 9 = q>0,S n 是其前 n 项 和 , 则 S 6 =________.  【解析】 由 a 1 =27,a 9 = 知 , =27 · q 8 , 又由 q>0, 解得 q= , 所以 S 6 = 答案 : 3.( 必修 5P39T14(1) 改编 ) 已知数列 : , , ,…, , 则其前 n 项和关于 n 的 表达式为 ____________.  【解析】 设所求的前 n 项和为 S n , 则 S n = +…+ 　 ①, S n = +…+ 　 ②. ①-② 得 S n = 即 S n =2- 答案 : 2-