2010年高考试题—数学文(四川) 13页

绝密★启用前 ‎2010年普通高等学校招生全国统一考试(四川卷)‎ 数学(文史类)‎ 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页，第Ⅱ卷3至1 0‎ 页．满分150分。考试时间120分钟。考试结束后，将本试卷和答题卡一并交回.‎ 第Ⅰ卷 注意事项： ‎ ‎1．答第1卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.‎ ‎2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．不能答在试卷上． ‎ ‎3。本试卷共1 2小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的。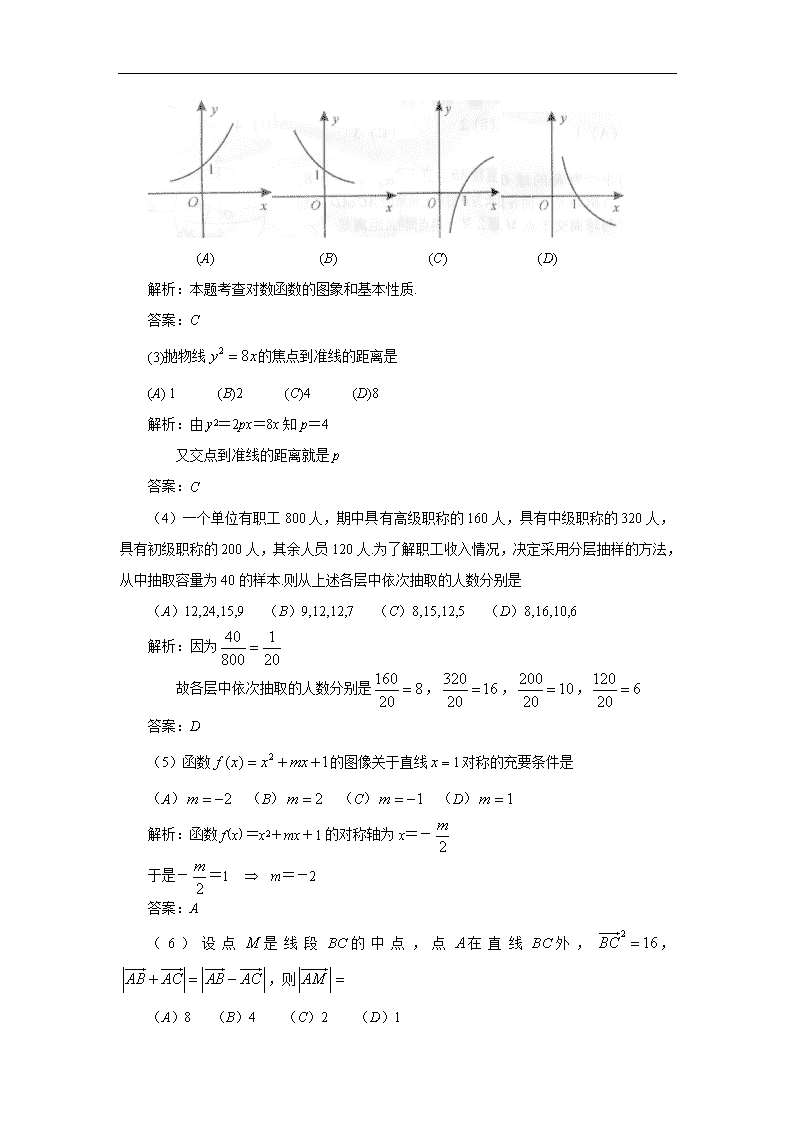‎ 参考公式： ‎ 如果事件A、B互斥，那么 球的表面积公式 P(A+B) =P(A)+P(B) ‎ 如果事件A、B相互独立，那么 其中R表示球的半径 P(A·B)=P(A)·P(B) 球的体积公式 如果事件A在一次试验中发生的概率是p，那么 ‎ 在n次独立重复试验中事件A恰好发生k次的概率 其中R表示球的半径 一、选择题 ‎(1)设集合A={3，5，6，8}，集合B={4，5， 7，8}，则A∩B等于 ‎(A){3，4，5，6，7，8} (B){3，6} (C) {4，7} (D){5，8}‎ 解析：集合A与集合B中的公共元素为5,8‎ 答案：D ‎(2)函数y=log2x的图象大致是 ‎(A) (B) (C) (D)‎ 解析：本题考查对数函数的图象和基本性质.‎ 答案：C ‎(3)抛物线的焦点到准线的距离是 ‎(A) 1 (B)2 (C)4 (D)8‎ 解析：由y2＝2px＝8x知p＝4‎ ‎ 又交点到准线的距离就是p 答案：C ‎（4）一个单位有职工800人，期中具有高级职称的160人，具有中级职称的320人，具有初级职称的200人，其余人员120人.为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是 ‎（A）12,24,15,9 （B）9,12,12,7 （C）8,15,12,5 （D）8,16,10,6‎ 解析：因为 ‎ 故各层中依次抽取的人数分别是，，，‎ 答案：D ‎（5）函数的图像关于直线对称的充要条件是 ‎（A） （B） （C） （D）‎ 解析：函数f(x)＝x2＋mx＋1的对称轴为x＝－‎ 于是－＝‎1 Þ m＝－2‎ 答案：A ‎（6）设点是线段的中点，点在直线外，， ，则 ‎（A）8 （B）4 （C）2 （D）1‎ 解析：由＝16，得|BC|＝4‎ ‎＝4‎ 而 故2‎ 答案：C ‎（7）将函数的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是 ‎（A） （B）‎ ‎（C） （D）‎ 解析：将函数的图像上所有的点向右平行移动个单位长度，所得函数图象的解析式为y＝sin(x－)‎ ‎ 再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是.‎ 答案：C ‎（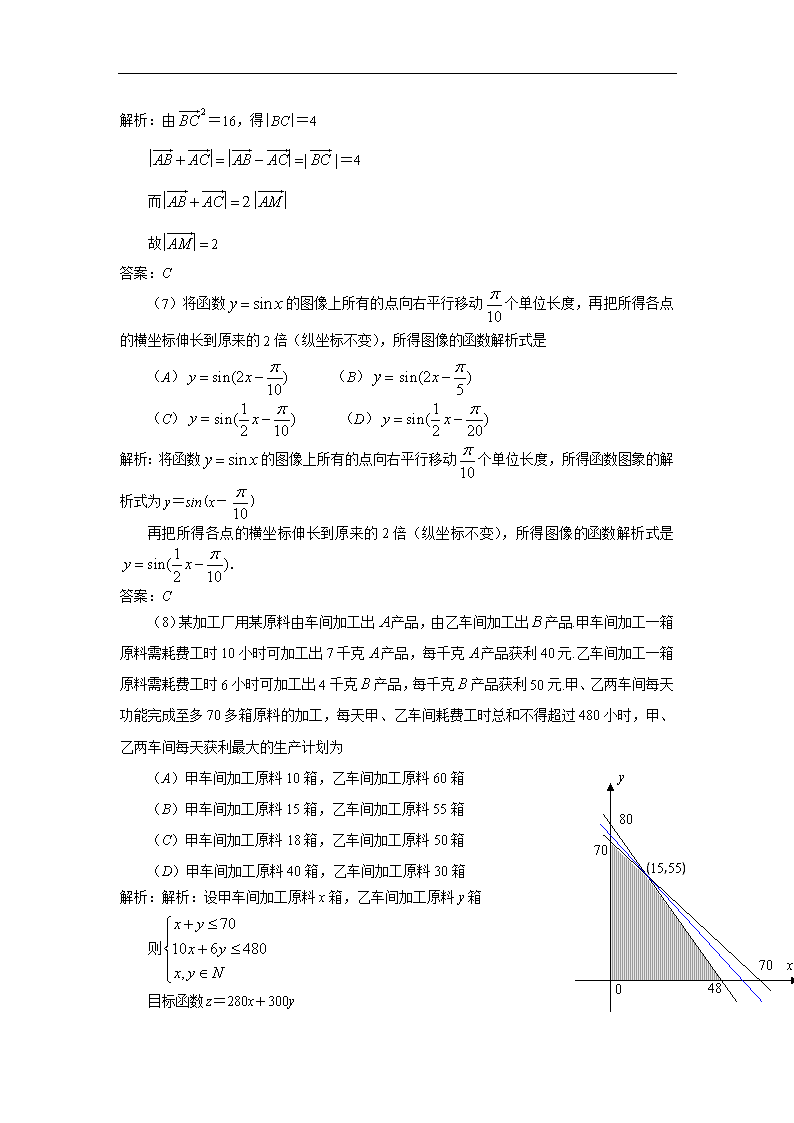8）某加工厂用某原料由车间加工出产品，由乙车间加工出产品.甲车间加工一箱原料需耗费工时10小时可加工出‎7千克产品，每千克产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出‎4千克产品，每千克产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工，每天甲、乙车间耗费工时总和不得超过480小时，甲、乙两车间每天获利最大的生产计划为 y ‎0‎ x ‎70‎ ‎48‎ ‎80‎ ‎70‎ ‎(15,55)‎ ‎（A）甲车间加工原料10箱，乙车间加工原料60箱 ‎（B）甲车间加工原料15箱，乙车间加工原料55箱 ‎（C）甲车间加工原料18箱，乙车间加工原料50箱 ‎（D）甲车间加工原料40箱，乙车间加工原料30箱 解析：解析：设甲车间加工原料x箱，乙车间加工原料y箱 则 目标函数z＝280x＋300y 结合图象可得：当x＝15,y＝55时z最大 本题也可以将答案逐项代入检验.‎ 答案：B ‎（9）由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是 ‎（A）36 （B）32 （C）28 （D）24‎ 解析：如果5在两端，则1、2有三个位置可选，排法为2×＝24种 ‎ 如果5不在两端，则1、2只有两个位置可选，3×＝12种 ‎ 共计12＋24＝36种 答案：A ‎（10）椭圆的右焦点为F，其右准线与轴的交点为．在椭圆上存在点P满足线段AP的垂直平分线过点F，则椭圆离心率的取值范围是 ‎（A）（0，] （B）（0，] （C）[，1） （D）[，1）‎ 解析：由题意，椭圆上存在点P，使得线段AP的垂直平分线过点，‎ 即F点到P点与A点的距离相等 而|FA|＝‎ ‎ |PF|∈[a－c,a＋c]‎ 于是∈[a－c,a＋c]‎ 即ac－c2≤b2≤ac＋c2‎ ‎∴‎ Þ 又e∈(0,1)‎ 故e∈‎ 答案：D ‎（11）设，则的最小值是 ‎（A）1 （B）2 （C）3 （D）4‎ 解析：‎ ‎＝‎ ‎＝‎ ‎≥2＋2＝4‎ 当且仅当ab＝1,a(a－b)＝1时等号成立 如取a＝,b＝满足条件.‎ 答案：D ‎（12）半径为的球的直径垂直于平面，垂足为，是平面内边长为的正三角形，线段、分别与球面交于点、，那么、两点间的球面距离是 ‎（A） （B）‎ ‎（C） （D）‎ 解析：由已知，AB＝2R,BC＝R,故tan∠BAC＝‎ cos∠BAC＝‎ 连结OM，则△OAM为等腰三角形 AM＝2AOcos∠BAC＝，同理AN＝，且MN∥CD 而AC＝R,CD＝R 故MN：CD＝AN:AC Þ MN＝，‎ 连结OM、ON，有OM＝ON＝R 于是cos∠MON＝‎ 所以M、N两点间的球面距离是 答案：A 二、填空题 ‎(13)(x－)4的展开式中的常数项为______________(用数字作答)‎ 解析：展开式的通项公式为Tr＋1＝‎ ‎ 取r＝2得常数项为C42(－2)2＝24‎ 答案：24‎ ‎(14)直线与圆相交于A、B两点，则 .‎ 解析：方法一、圆心为(0,0)，半径为2‎ 圆心到直线的距离为d＝‎ 故 得|AB|＝2 答案：2 ‎（15）如图，二面角的大小是60°，线段.，‎ 与所成的角为30°.则与平面所成的角的正弦值是 .‎ 解析：过点A作平面β的垂线，垂足为C，在β内过C作l的垂线.垂足为D 连结AD，有三垂线定理可知AD⊥l，‎ 故∠ADC为二面角的平面角，为60°‎ C D 又由已知，∠ABD＝30°‎ 连结CB，则∠ABC为与平面所成的角 设AD＝2，则AC＝，CD＝1‎ AB＝＝4‎ ‎∴sin∠ABC＝‎ 答案：‎ ‎（16）设S为复数集C的非空子集.若对任意，都有，则称S为封闭集。下列命题：‎ ‎①集合S＝{a＋bi|（为整数，为虚数单位）}为封闭集；‎ ‎②若S为封闭集，则一定有；‎ ‎③封闭集一定是无限集；‎ ‎④若S为封闭集，则满足的任意集合也是封闭集.‎ 其中真命题是 （写出所有真命题的序号）‎ 解析：直接验证可知①正确.‎ 当S为封闭集时，因为x－y∈S，取x＝y，得0∈S，②正确 对于集合S＝{0}，显然满足素有条件，但S是有限集,③错误 取S＝{0}，T＝{0,1}，满足,但由于0－1＝－1ÏT，故T不是封闭集，④错误 答案：①②‎ 三、 解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。‎ ‎（17）（本小题满分12分）‎ 某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为.甲、乙、丙三位同学每人购买了一瓶该饮料。‎ ‎（Ⅰ）求三位同学都没有中奖的概率；‎ ‎（Ⅱ）求三位同学中至少有两位没有中奖的概率.‎ ‎（18）（本小题满分12分）‎ 在正方体ABCD－A′B′C′D′中，点M是棱AA′的中点，点O是对角线BD′的中点.‎ ‎（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；‎ ‎（Ⅱ）求二面角M－BC′－B′的大小；‎ ‎（19）（本小题满分12分）‎ ‎（Ⅰ）证明两角和的余弦公式；‎ ‎ 由推导两角和的正弦公式.‎ ‎（Ⅱ）已知，求 ‎（20）（本小题满分12分）‎ ‎ 已知等差数列的前3项和为6，前8项和为-4。‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设，求数列的前n项和 ‎（21）（本小题满分12分）‎ 已知定点A(－1，0)，F(2，0)，定直线l：x＝，不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E，过点F的直线交E于B、C两点，直线AB、AC分别交l于点M、N ‎（Ⅰ）求E的方程；‎ ‎（Ⅱ）试判断以线段MN为直径的圆是否过点F，并说明理由.‎ ‎（22）（本小题满分14分）‎ 设（且），g(x)是f(x)的反函数.‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）当时，恒有成立，求t的取值范围；‎ ‎（Ⅲ）当0＜a≤时，试比较f(1)+f(2)+…+f(n)与的大小，并说明理由.‎