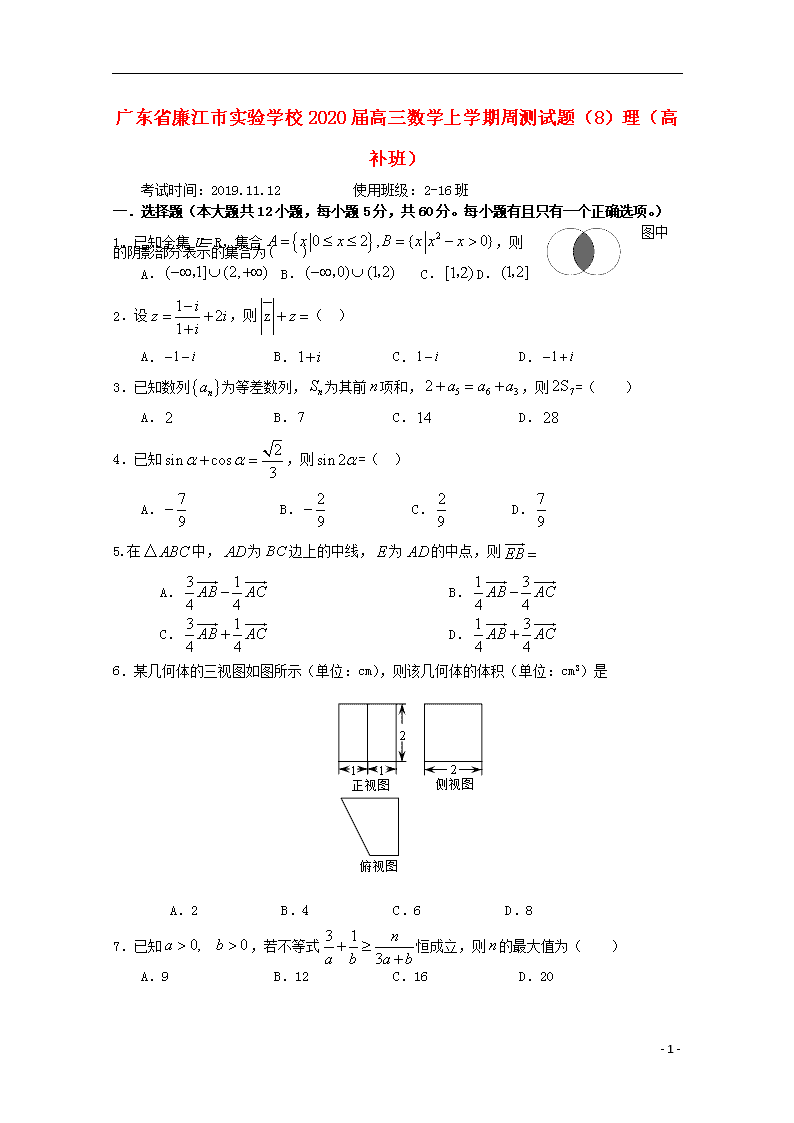广东省廉江市实验学校2020届高三数学上学期周测试题8理（高补班）含解析 9页

- 1 - 广东省廉江市实验学校 2020 届高三数学上学期周测试题（8）理（高 补班） 考试时间：2019.11.12 使用班级：2-16 班 一．选择题（本大题共 12 小题，每小题 5 分，共 60 分。每小题有且只有一个正确选项。） 1．已知全集 U＝R，集合   20 2 , { 0}A x x B x x x      ，则 图中 的阴影部分表示的集合为( ) A． ( 1] (2, )  ， B． ( 0) (1 2) ， ， C．[1 )2， D． (1 2]， 2．设 1 21 iz ii   ，则  z — z （ ） A． 1 i  B．1 i C．1 i D． 1 i  3．已知数列 na 为等差数列， nS 为其前 n 项和， 5 6 32 a a a  ，则 72S =（ ） A． 2 B． 7 C．14 D． 28 4．已知 2sin cos 3    ，则sin 2 =（ ） A． 7 9  B． 2 9  C． 2 9 D． 7 9 5.在 ABC△ 中， AD 为 BC 边上的中线， E 为 AD 的中点，则 EB  A． 3 1 4 4AB AC  B． 1 3 4 4AB AC  C． 3 1 4 4AB AC  D． 1 3 4 4AB AC  6．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是 A．2 B．4 C．6 D．8 7．已知 0, 0a b  ，若不等式 3 1 3 n a b a b    恒成立，则 n 的最大值为（ ） A．9 B．12 C．16 D．20 - 2 - 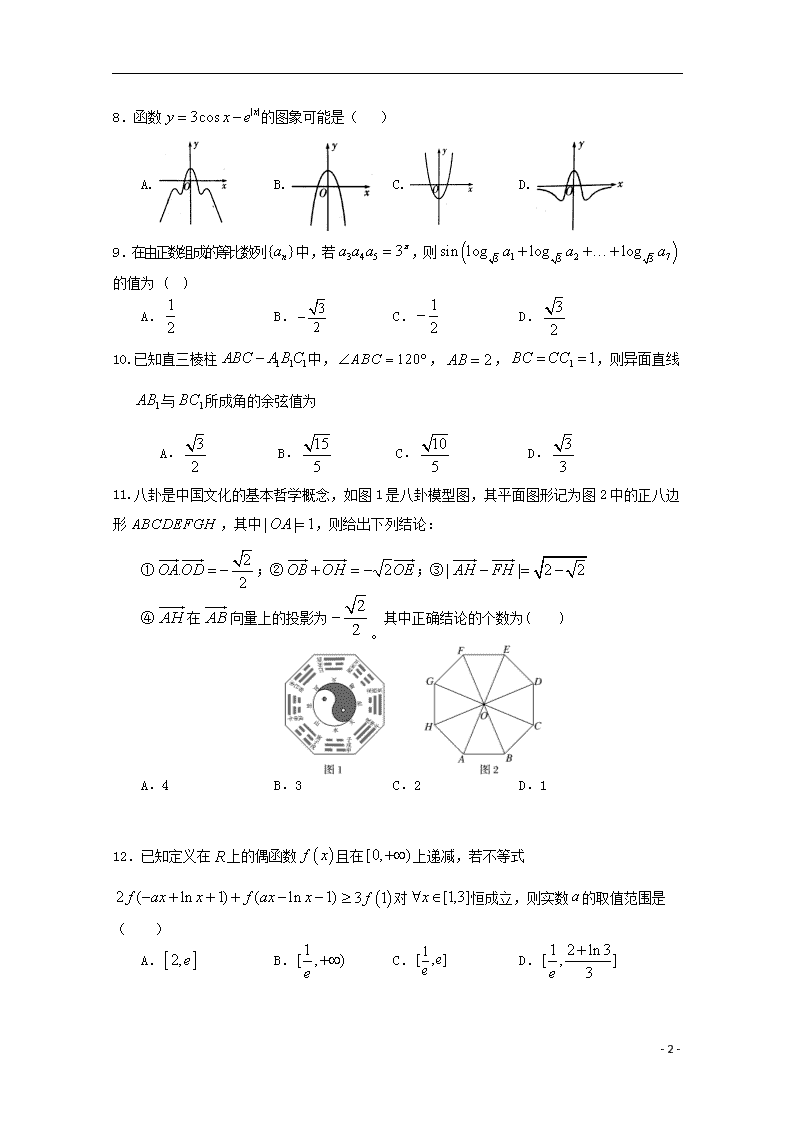8．函数 ||cos3 xexy  的图象可能是（ ） A. B. C. D. 9．在由正数组成的等比数列{ }na 中，若 3 4 5 3a a a  ，则  1 2 73 3 3sin log log loga a a  的值为 ( ) A． 1 2 B． 3 2  C． 1 2  D． 3 2 10.已知直三棱柱 1 1 1ABC A B C 中， 120ABC   ， 2AB  ， 1 1BC CC  ，则异面直线 1AB 与 1BC 所成角的余弦值为 A． 3 2 B． 15 5 C． 10 5 D． 3 3 11.八卦是中国文化的基本哲学概念，如图 1 是八卦模型图，其平面图形记为图 2 中的正八边 形 ABCDEFGH ，其中| | 1OA  ，则给出下列结论： ① 2. 2OAOD    ；② 2OB OH OE     ；③| | 2 2AH FH    ④ AH  在 AB  向量上的投影为 2 2  。 其中正确结论的个数为( ) A．4 B．3 C．2 D．1 12．已知定义在 R 上的偶函数  f x 且在[0, ) 上递减，若不等式 2 ( ln 1) ( ln 1)f ax x f ax x       3 1f 对 ]3,1[x 恒成立，则实数 a 的取值范围是 （ ） A． 2,e B． 1[ , )e  C． 1[ , ]ee D． 1 2 ln3[ , ]3e  - 3 - 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分。） 13．已知函数 xxf ln)(  与直线 axy  相切，则 a 的取值是 . 14．《九章算术》中的“两鼠穿墙题”是我国数学的古典名题：“今有垣厚若干尺，两鼠对穿， 大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半，问何日相逢，各穿几何？”题意是： “有两只老鼠从墙的两边打洞穿墙，大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也 进一尺，以后每天减半．”如果一墙厚 10 尺，请问两只老鼠最少在第______天相遇． 15．已知函数     2sin 0f x x     满足 24f      ，   0f   ，且  f x 在区间 ,4 3       上单调，则 的值有_________个. 16．已知函数 axxxf 32)( 2  ， 1 2)(  xxg ．若对 ]3,0[1 x ，总 ]3,2[2 x ，使得 )(|)(| 21 xgxf  成立，则实数的取值集合为____ 三、解答题（本大题共 6 个小题，共 70 分。） 17.（本小题 10 分）已知数列{an}为等比数列，数列{bn}为等差数列，且 b1＝a1＝1，b2＝a1＋ a2，a3＝2b3－6. (1)求数列{an}，{bn}的通项公式； (2)设 cn＝ 1 bnbn＋2 ，数列{cn}的前 n 项和为 Tn，证明：1 5 ≤Tn<1 3 . 18．（本小题 12 分）已知函数 2( ) cos 2 cos2 ( )3f x x x x R       (1)求函数 ( )f x 的单调递增区间； (2) ABC 内角 , ,A B C 的对边分别为 , ,a b c ，若 3( )2 2 Bf   ， 1b  ， 3c  ，且 a b ， 试求角 B 和角C . 19.（本小题 12 分）如图 1,在直角梯形 ABCD 中, 90ADC   ， / /CD AB , 2, 1AB AD CD   ，将 ADC 沿 AC 折起，使平面 ADC  平面 ABC ,得到 几何体 D ABC ,如图 2 所示. - 4 - （1）求证: 平面 ACD ； （2）求二面角 D-AB-C 的正弦值。 20. （ 本 小 题 12 分 ） 在 △ ABC 中 ， 角 A ， B ， C 所 对 的 边 分 别 为 a ， b ， c ， 且 12cos2sin2 2       CBA ， a ＝1，b＝2。 (1)求∠C 和边 c； (2)若 BCBM 4 , BABN 3 ,且点 P 为△BMN 内切圆上一点， 求 222 PCPBPA  的最大值。 21（本小题 12 分）.已知椭圆C : 2 2 2 2 1,( 0)x y a ba b     的两个焦点分别为 1 2( 1,0), (1,0)F F , 且椭圆C 经过点 4 1( , )3 3P . (Ⅰ)求椭圆C 的离心率； (Ⅱ)过点 2F 的直线l 与椭圆 C 相交于 P Q、 两点,且 1 1F P FQ  ,求直线l 的方程. 22.（本小题 12 分）已知函数 ( ) ln 1( )f x ax x a R    . （Ⅰ）求 ( )f x 的单调区间； （Ⅱ）若 0a  ，令 3 2( ) ( 1) 2 xg x f tx x     ，若 1x ， 2x 是 ( )g x 的两个极值点，且    1 2 0g x g x  ，求正实数t 的取值范围. - 5 - 周测 8 参考答案：选择题： DBDAA CCBDC CD 二．填空题： 13. e 1 ； 14. 4 ； 15. 9 ； 16. }3 1{ 。 三．解答题： 17.解 设数列{an}的公比为 q，数列{bn}的公差为 d， 由题意得 1＋d＝1＋q，q2＝2(1＋2d)－6，解得 d＝q＝2， 所以 an＝2n－1，bn＝2n－1. -------------5 分 (2)证明 因为 cn＝ 1 bnbn＋2 ＝ 1 2n－12n＋3 ＝1 4 1 2n－1 － 1 2n＋3 ， 所以 Tn＝1 4 1－1 5 ＋ 1 3 －1 7 ＋…＋ 1 2n－3 － 1 2n＋1 ＋ 1 2n－1 － 1 2n＋3 ＝1 4 1＋1 3 － 1 2n＋1 － 1 2n＋3 ＝1 3 －1 4 1 2n＋1 ＋ 1 2n＋3 ， 因为1 4 1 2n＋1 ＋ 1 2n＋3 >0，所以 Tn<1 3 .又因为 Tn 在[1，＋∞)上单调递增， 所以当 n＝1 时，Tn 取最小值 T1＝1 5 ，所以1 5 ≤Tn<1 3 . ---------------10 分 18．（1） 2 3 3( ) cos 2 cos2 sin 2 cos2 3sin 23 2 2 3f x x x x x x                 ， …………3 分 故函数 ( )f x 的递增区间为 5, ( )12 12k k k        Z .………………5 分 （2） 3 13sin , sin2 3 2 3 2 Bf B B                        ， 20 , , ,3 3 3 3 6 6B B B B                即 ， ………………7 分 由正弦定理得： 1 3 sin sinsin 6 a A C  ， 3sin 2C  ， 0 C   ， 3C   或 2 3  .………………9 分 - 6 - 当 3c  时， 2A  ：………………10 分 当 2 3C  时， 6A  （与已知 a b 矛盾，舍）…………11 分 所以 ,6 3B C   .即为所求………………12 分 19.（1）证明：在图 1 中，由题意知，AC=BC=2 2 BCAC ， ∴AC2+BC2=AB2，∴AC⊥BC………………2 分 取 AC 中点 O，连接 DO，则 DO⊥AC，又平面 ADC⊥平面 ABC， 且平面 ADC∩平面 ABC=AC，DO⊂平面 ACD，从而 OD⊥平面 ABC，………………4 分 ∴OD⊥BC 又 AC⊥BC，AC∩OD=O，∴BC⊥平面 ACD………………6 分 (2）过 D 作 ACDO  于 O，再过 O 作 ABOF  于 F，连接 DF，易知 DFO 为二面角 CABD  的平面角 ..................9 分 易知 2 3,2 1,2 2  DFOFDO , 2 6sin  DF DODFO 即为所求二面角的正弦 值。………………12 分 （注：坐标法，对应给分）。 20 题 解析：(1)∵2sin2A＋B 2 ＋cos 2C＝1，∴cos 2C＝sin2A＋B 2 ＝cos(A＋B)＝－cos C， ∴2cos2C＋cos C－1＝0，∴cos C＝1 2 或 cos C＝－1，∵C∈(0，π)，∴cos C＝1 2 ，∴C ＝π 3 ．由余弦定理得 c＝ a2＋b2－2abcos C＝ 3． ------------6 分 （2）建立坐标系，由（1）A     )1,0(,0,0,0,3 CB ，由 BCBM 4 , BABN 3 知  0,3),4,0( NM ，△BMN 的内切圆方程为：     111 22  yx ，设 ),( yxP ，则令    2,0,sin1 cos1       y x         22 2 2 22 2 2 2 2 2 3 1 3 3 2 3 2 4 11 2 3 4sin 6 2 3 cos 11 2 3 64 24 3 sin 11 2 3 64 24 3 PA PB PC x y x y x y x y x y                                     -------------------------12 分 - 7 - 21.解: (Ⅰ) 2 2 2 2 1 2 4 1 4 12 1 1 2 23 3 3 3a PF PF                               所以, 2a  . 又由已知, 1c  , 所以椭圆 C 的离心率 1 2 22 ce a    ------4 分   由  知椭圆 C 的方程为 2 2 12 x y  . 当直线l 的斜率不存在时,其方程为 1x  , 不符合题意; 当直线的斜率存在时,设直线l 的方程为 ( 1)y k x  . 由 2 2 ( 1) 12 y k x x y     得 2 2 2 2(2 1) 4 2( 1) 0k x k x k     . ----------6 分 设 1 1 2 2( ) ( )P x y Q x y， ， ， ,则 2 2 1 2 1 2 1 1 1 1 2 22 2 4 2( 1) ( 1 ) ( 1 )2 1 2 1 k kx x x x F P x y FQ x yk k          ， ， ， ， ， 因为 1 1F P FQ  ,所以 1 1 0F P FQ   ,即 2 1 2 1 2 1 2 1 2 1 2( 1)( 1) ( ) 1 ( 1)( 1)x x y y x x x x k x x          2 2 2 1 2 1 2( 1) ( 1)( ) 1k x x k x x k       2 2 7 1 02 1 k k   , ----------19 分 解得 2 1 7k  ,即 7 7k   . 故直线l 的方程为 7 1 0x y   或 7 1 0x y   . ------12 分 22.解：（Ⅰ）由 ( ) ln 1f x ax x   ， (0, )x  ，则 1 1( ) axf x a x x     ，……………… 1 分 当 0a  时，则 ( ) 0f x  ，故 ( )f x 在 (0, ) 上单调递减；………………2 分 当 0a  时，令 1( ) 0f x x a     ，所以 ( )f x 在 10, a      上单调递减，在 1 ,a     上单 调递增.………………3 分综上所述：当 0a  时， ( )f x 在 (0, ) 上单调递减； 当 0a  时， ( )f x 在 10, a      上单调递减，在 1 ,a     上单调递增.………………4 分 - 8 - （Ⅱ） 3 2 2( ) ( 1) ln( 1)2 2 x xg x f tx txx x        ， 故 2 2 2 4 4( 1)( ) ( 2) 1 ( 2) ( 1) t tx tg x x tx x tx          ，………………5 分 当 1t  时， ( ) 0g x  恒成立，故 ( )g x 在 (0, ) 上单调递减，不满足 ( )g x 有两个极值 点，故 0 1t  .………………6 分 令 ( ) 0g x  ，得两个极值点 t txt tx  12,12 21 ， 由函数的定义域得： 1 12 t t t    且 1 12 2 0 2 t tt       1 12 t  ；………………7 分 故        1 2 1 2 1 2 1 2 2 2ln 1 ln 12 2 x xg x g x tx txx x              1 2 1 2 2 1 2 1 2 1 2 1 2 4 4 ln 12 4 x x x x t x x t x xx x x x            2 24( 1) 2ln(2 1) 2 ln(2 1)2 1 2 1 t t tt t         ………………8 分 令 2 1u t  ，由 10 2t  或 1 12 t  得 ( 1,0) (0,1)u    令 22( ) 2 lnh u uu    ， ( 1,0) (0,1)u    ………………9 分 当 ( 1,0)u   时， 2 2 2 2 2( ) 2 ln ( ) 0h u u h uu u u        ， 则 ( )h u 在 ( 1,0) 上单调递增，故 ( ) ( 1) 4 0h u h    ， 则 10 2t  时    1 2 0g x g x  成立；………………10 分 当 (0,1)u  时， 2 2 2 2( ) 2 2ln ( ) 0h u u h uu u u        ，则 ( )h u 在 (0,1) 上单调递增， 故 ( ) (1) 0h u h  ，则 1 12 t     1 2 0g x g x  ；综上所述： 10, 2t     .……12 分 - 9 -