古典概型教案1 6页

‎ ‎ 古典概型 一，教材的地位和作用 本节课是中数学3（必修）第三章概率的第二节古典概型的第一课时，是在学习随机事件的概率之后，几何概型之前，文科生不学习排列组合的情况下教学的 。古典概型是一种特殊的数学模型，也是一种最基本的概率模型，在概率论中占有相当重要的地位。‎ ‎ 学好古典概型可以为其它概率的学习奠定基础，同时有利于理解概率的概念，有利于计算一些事件的概率，有利于解释生活中的一些问题。‎ 二，教学目标 ‎1、知识目标 ‎(1)理解古典概型及其概率计算公式，‎ ‎(2)会用列举法计算一些随机事件所含的基本事件数及事件发生的概率。 ‎ ‎2、能力目标 根据本节课的内容和学生的实际水平，通过抽牌游戏让学生理解古典概型的定义，引领学生探究古典概型的概率计算公式，归纳出求基本事件数的方法—列举法。‎ ‎3 、情感目标 树立从具体到抽象、从特殊到一般的辩证唯物主义观点，培养学生用随机的观点来理性的理解世界， 使得学生在体会概率意义的同时，感受与他人合作的重要性以及初步形成实事求是地科学态度和锲而不舍的求学精神。鼓励学生通过观察类比提高发现问题、分析问题、解决问题的能力，增强学生数学思维情趣，形成学习数学知识的积极态度。 ‎ 三，教学的重点和难点 重点：理解古典概型的概念及利用古典概型求解随机事件的概率。 ‎ 难点：如何判断一个试验的概率模型是否为古典概型，弄清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数。 ‎ 四，教具 ‎ 计算机多媒体，黑板，粉笔，教棒 五，教学方法 ‎ 探究式与讲授式相结合 六，教学过程 1， 教学引入 ‎ 前面我们学习了随机事件及其概率，今天我们将学习古典概型，古典概型是最简单，而且最早被人们所认识的一种概率模型，大约在1812年著名数学家拉普拉斯就已经注意并研究了古典概型概率的计算。下面先看一个抽牌游戏。‎ ‎ 抽牌游戏: ‎ 6‎ ‎ ‎ ‎ 有红桃1,2,3和黑桃4,5这5张扑克牌,将其牌点向下置于桌上,现从中任意抽取一张,那么抽到的牌为红桃的概率有多大?‎ ‎ 为了解决这个问题，我们首先介绍几个基本概念。‎ 1， 新课讲授 一， 基本概念: ‎ 1， 基本事件：‎ 在一次试验中可能出现的每一基本结果称为基本事件 如：刚才抽牌游戏中抽到红桃A就是一个基本事件 ‎2，等可能基本事件 ‎ 若在一次试验中，每个基本事件发生的可能性都相同,则称这些基本事件为等可能事件。‎ ‎ 如: 刚才抽牌游戏中由于是任意抽取，所以抽到每一张牌的可能性都相同。‎ ‎3，古典概型 满足以下两个特点的随机试验的概率模型称为古典概型 ‎⑴所有的基本事件只有有限个 ‎⑵每个基本事件的发生都是等可能的 ‎ 下面给出两个随机试验，请同学们判断这两个随机试验的概率模型是不是古典概型。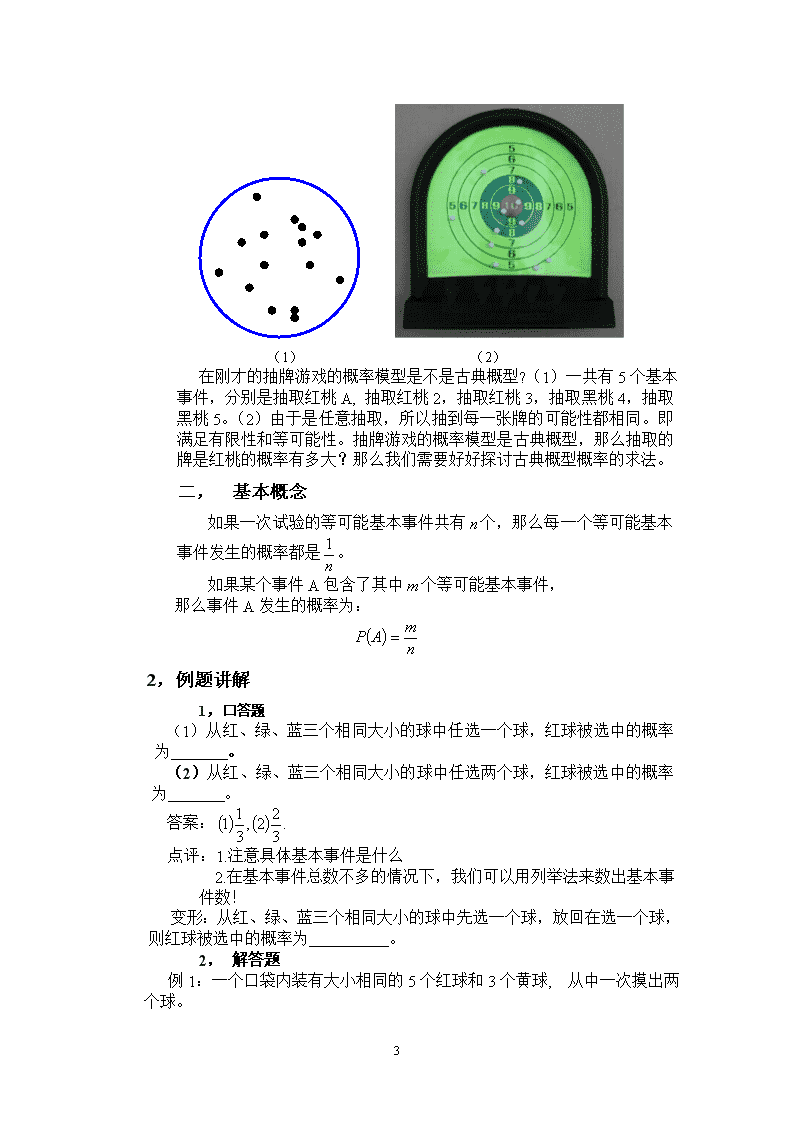‎ ‎ 1）向一个圆面内随机地投射一个点，如果该点落在圆内任意一点都是等可能的，你认为这是古典概型吗?为什么？‎ 答案：不是古典概型。因为试验的所有可能结果是圆面内所有的点，试验的所有可能结果数是无限的，虽然每一个试验结果出现的“可能性相同”，但这个试验不满足古典概型的第一个条件有限性。 ‎ ‎2）如图，某同学随机地向一靶心进行射击，这一试验的结果只有有限个：命中10环、命中9环……命中5环和不中环。你认为这是古典概型吗？为什么？ ‎ 答案：不是古典概型。不是古典概型，因为试验的所有可能结果只有7个，而命中10环、命中9环……命中5环和不中环的出现不是等可能的，即不满足古典概型的第二个条件等可能性。 ‎ 6‎ ‎ ‎ ‎ ‎ ‎ （1） （2）‎ ‎ 在刚才的抽牌游戏的概率模型是不是古典概型?（1）一共有5个基本事件，分别是抽取红桃A, 抽取红桃2，抽取红桃3，抽取黑桃4，抽取黑桃5。（2）由于是任意抽取，所以抽到每一张牌的可能性都相同。即满足有限性和等可能性。抽牌游戏的概率模型是古典概型，那么抽取的牌是红桃的概率有多大？那么我们需要好好探讨古典概型概率的求法。‎ 一， 基本概念 如果一次试验的等可能基本事件共有个，那么每一个等可能基本事件发生的概率都是。 ‎ 如果某个事件A包含了其中个等可能基本事件，‎ 那么事件A发生的概率为： ‎ ‎2，例题讲解 1， 口答题 ‎（1）从红、绿、蓝三个相同大小的球中任选一个球，红球被选中的概率为 。‎ ‎（2）从红、绿、蓝三个相同大小的球中任选两个球，红球被选中的概率为 。‎ 答案：‎ 点评：1.注意具体基本事件是什么 ‎ 2.在基本事件总数不多的情况下，我们可以用列举法来数出基本事件数！‎ 变形：从红、绿、蓝三个相同大小的球中先选一个球，放回在选一个球，则红球被选中的概率为 。‎ 2， 解答题 ‎ 例1：一个口袋内装有大小相同的5个红球和3个黄球, 从中一次摸出两个球。‎ 6‎ ‎ ‎ ‎ ⑴问共有多少个基本事件；‎ ‎⑵求摸出两个球都是红球的概率；‎ ‎⑶求摸出的两个球都是黄球的概率；‎ ‎⑷求摸出的两个球一红一黄的概率。‎ 解： ⑴分别对红球编号为1、2、3、4、5号，对黄球编号6、7、8号，从中任取两球，有如下等可能基本事件，列举如下：‎ ‎（1，2）、（1，3）、（1，4）、（1，5）、（1，6）、（1，7）、（1，8）‎ ‎ （2，3）、（2，4）、（2，5）、（2，6）、（2，7）、（2，8）‎ ‎ （3，4）、（3，5）、（3，6）、（3，7）、（3，8）‎ ‎ （4，5）、（4，6）、（4，7）、（4，8） ‎ ‎ （5，6）、（5，7）、（5，8） ‎ ‎ （6，7）、（6，8） ‎ ‎ （7，8） ‎ ‎ ‎ ‎ 共28个基本事件。 28‎ ‎（2）设“摸出两个球都是红球”为事件A，则A中包含的基本事件有10个，‎ ‎ 因此 ‎ ‎ ‎（3）设“摸出两个球都是黄球” 为事件B，则事件B中包含的基本事件有3个，‎ ‎ 因此 ‎ ‎ ‎ ‎ ‎ （4）设“摸出两个球一红一黄” 为事件C，则事件C包含的基本事件有15个，‎ ‎ 因此 ‎ ‎ ‎ ‎‎（5，6）、（5，7）、（5，8） ‎ ‎（1，2）、（1，3）、（1，4）、（1，5）、（1，6）、（1，7）、（1，8）‎ ‎（2，3）、（2，4）、（2，5）、（2，6）、（2，7）、（2，8）‎ ‎(1) （3，4）、（3，5）、（3，6）、（3，7）、（3，8） (3)‎ ‎（4，5）、（4，6）、（4，7）、（4，8） ‎ ‎（6，7）、（6，8） ‎ ‎(2 ) （7，8） ‎ 答: ⑴共有28个基本事件； ‎ ‎ ⑵摸出两个球都是红球的概率为 6‎ ‎ ‎ ‎ ⑶摸出的两个球都是黄球的概率为;‎ ‎ ⑷摸出的两个球一红一黄的概率为.‎ ‎ 点评：注意解题格式:一设二求三答!‎ 通过对摸球问题的探讨，你能总结出求古典概型概率的方法和步骤吗？‎ 方法总结：‎ 首先判断是否是古典概型 ‎⑴求基本事件的总数;‎ ‎ ⑵求事件A包含的基本事件的个数;‎ ‎ ⑶代入计算公式：‎ ‎3，巩固练习 ‎1. 甲，乙两人是同月同日生的概率为 .‎ ‎2.用三种不同颜色给三个矩形涂色,每个矩形只涂一种颜色,求:‎ ‎ (1) 3个矩形颜色都相同的概率;‎ ‎ (2) 3个矩形颜色都不同的概率.‎ 点评: 会总结求基本事件的总数和事件A包含的基本事件的个数的方法。‎ 思考：‎ ‎1.若基本事件很多的时候,还能用枚举法吗?是否还有其他方法呢?‎ ‎2.基本事件的个数是有限的时候是古典概型,那是否还有基本事件是无限的呢?‎ ‎4，课堂小结：‎ 本节课主要学习了古典概型的概念及古典概型概率的求法。要求同学们能够会判断一个试验的概率模型是否为古典概型，掌握古典概型概率求法的格式与步骤。‎ 七，板书设计 ‎ 古典概型 ‎ 一，基本概念 二，基本方法 ‎1，基本事件 1，古典概型概率的求法 ‎2，等可能事件 2，格式：一设二求三答 ‎ ‎ ‎3，古典概型 3，步骤：‎ 6‎ ‎ ‎ ‎ ‎ 八，教后感 ‎ ‎ 本节课的教学通过抽牌游戏贯穿整个教学，再通过具体问题的提出和解决，来激发学生的学习兴趣，调动学生的主体能动性，让每一个学生充分地参与到学习活动中来。 在基本事件和等可能事件的基础上引出古典概型的概念，由两个问题的提出进一步加深对古典概型的两个特点的理解；再通过学生的探究推导出古典概型的概率计算公式。这一过程不仅能够培养学生发现问题、分析问题、解决问题的能力，而且增强学生数学思维情趣，形成学习数学知识的积极态度 ‎ 在解决概率的计算上，教师鼓励学生尝试列举法和画出树状图，让学生感受求基本事件个数的一般方法，从而化解由于没有学习排列组合而学习概率这一教学困惑。由此，整个教学设计可以在教师的期盼中实施。 ‎ 6‎