2020高中数学 专题强化训练2 随机变量及其分布 新人教A版选修2-3 5页

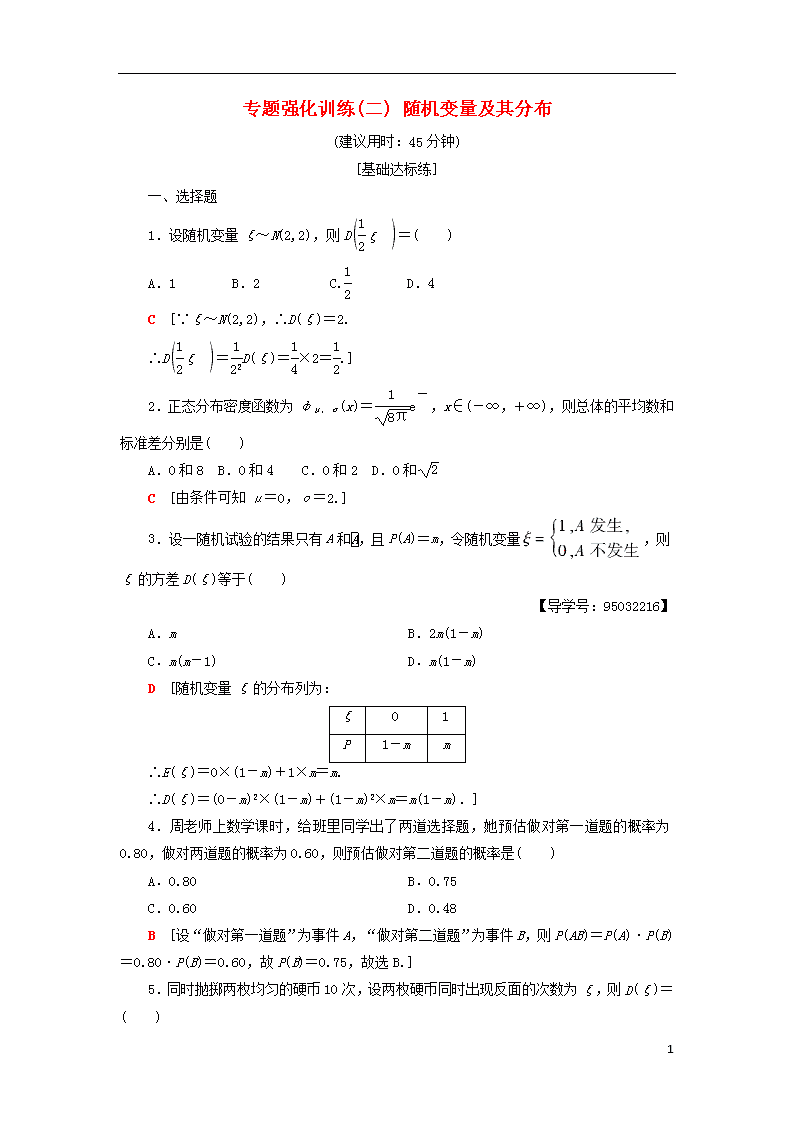
专题强化训练(二) 随机变量及其分布 ‎(建议用时：45分钟)‎ ‎[基础达标练]‎ 一、选择题 ‎1．设随机变量ξ～N(2,2)，则D＝(　　)‎ A．1　　　　B．‎2　‎　　　　C.　　　　D．4‎ C　[∵ξ～N(2,2)，∴D(ξ)＝2.‎ ‎∴D＝D(ξ)＝×2＝.]‎ ‎2．正态分布密度函数为φμ，σ(x)＝e，x∈(－∞，＋∞)，则总体的平均数和标准差分别是(　　)‎ A．0和8　B．0和‎4　‎　C．0和2　D．0和 C　[由条件可知μ＝0，σ＝2.]‎ ‎3．设一随机试验的结果只有A和，且P(A)＝m，令随机变量，则ξ的方差D(ξ)等于(　　)‎ ‎ 【导学号：95032216】‎ A．m　　　　　　　　 B．‎2m(1－m)‎ C．m(m－1) D．m(1－m)‎ D　[随机变量ξ的分布列为：‎ ξ ‎0‎ ‎1‎ P ‎1－m m ‎∴E(ξ)＝0×(1－m)＋1×m＝m.‎ ‎∴D(ξ)＝(0－m)2×(1－m)＋(1－m)2×m＝m(1－m)．]‎ ‎4．周老师上数学课时，给班里同学出了两道选择题，她预估做对第一道题的概率为0.80，做对两道题的概率为0.60，则预估做对第二道题的概率是(　　)‎ A．0.80 B．0.75‎ C．0.60 D．0.48‎ B　[设“做对第一道题”为事件A，“做对第二道题”为事件B，则P(AB)＝P(A)·P(B)＝0.80·P(B)＝0.60，故P(B)＝0.75，故选B.]‎ ‎5．同时抛掷两枚均匀的硬币10次，设两枚硬币同时出现反面的次数为ξ，则D(ξ)＝(　　)‎ 5‎ A. B. C. D．5‎ A　[两枚硬币同时出现反面的概率为×＝，故ξ～B，‎ 因此D(ξ)＝10××＝.]‎ 二、填空题 ‎6．袋中有4只红球3只黑球，从袋中任取4只球，取到1只红球得1分，取到1只黑球得3分，设得分为随机变量X，则P(X≤6)＝________. ‎ ‎【导学号：95032217】‎ 　[P(X≤6)＝P(X＝4)＋P(X＝6)＝＝.]‎ ‎7．甲、乙、丙三人到三个景点旅游，每人只去一个景点，设事件A为“三个人去的景点不相同”，B为“甲独自去一个景点”，则概率P(A|B)等于________．‎ 　[由题意可知，n(B)＝C22＝12，n(AB)＝A＝6.‎ 所以P(B|A)＝＝＝.]‎ ‎8．设随机变量X～B(2，p)，随机变量Y～B(3，p)，若P(X≥1)＝，则P(Y≥1)＝________. ‎ ‎【导学号：95032218】‎ 　[因为X～B(2，p)，所以P(X≥1)＝1－P(X＝0)＝1－C(1－p)2＝，解得p＝.‎ 又Y～B(3，p)，所以P(Y≥1)＝1－P(Y＝0)＝1－C(1－p)3＝.]‎ 三、解答题 ‎9．编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位，每位学生坐一个座位，设与座位编号相同的学生的人数是ξ，求E(ξ)和D(ξ)．‎ ‎[解]　ξ的所有可能取值为0,1,3，ξ＝0表示三位同学全坐错了，有2种情况，即编号为1,2,3的座位上分别坐了编号为2,3,1或3,1,2的学生，‎ 则P(ξ＝0)＝＝；‎ ξ＝1表示三位同学只有1位同学坐对了，‎ 则P(ξ＝1)＝＝；‎ 5‎ ξ＝3表示三位学生全坐对了，即对号入座，‎ 则P(ξ＝3)＝＝.‎ 所以，ξ的分布列为 ξ ‎0‎ ‎1‎ ‎3‎ P E(ξ)＝0×＋1×＋3×＝1；‎ D(ξ)＝×(0－1)2＋×(1－1)2＋×(3－1)2＝1.‎ ‎10．一个口袋内装有2个白球和2个黑球，那么 ‎(1)先摸出1个白球不放回，再摸出1个白球的概率是多少？‎ ‎(2)先摸出1个白球后放回，再摸出1个白球的概率是多少？ ‎ ‎【导学号：95032219】‎ ‎[解]　(1)设“先摸出1个白球不放回”为事件A，“再摸出1个白球”为事件B，则“先后两次摸出白球”为事件AB，“先摸一球不放回，再摸一球”共有4×3种结果．‎ 所以P(A)＝，P(AB)＝＝，所以P(B|A)＝＝.‎ 所以先摸出1个白球不放回，再摸出1个白球的概率为.‎ ‎(2)设“先摸出1个白球后放回”为事件A1，“再摸出1个白球”为事件B1，“两次都摸出白球”为事件A1B1，P(A1)＝，P(A1B1)＝＝，‎ 所以P(B1|A1)＝＝＝.‎ 所以先摸出1个白球后放回，再摸出1个白球的概率为.‎ ‎[能力提升练]‎ 一、选择题 ‎1．若随机变量ξ服从正态分布N(0,1)，已知P(ξ<－1.96)＝0.025，则P(|ξ|<1.96)＝(　　)‎ A．0.025　　　　　　　 B．0.050‎ C．0.950 D．0.975‎ 5‎ C　[由随机变量ξ服从正态分布N(0,1)，得P(ξ<1.96)＝1－P(ξ≤－1.96)，所以P(|ξ|<1.96)＝P(－1.96<ξ<1.96)＝1－2P(ξ≤－1.96)＝1－2P(ξ<－1.96)＝1－2×0.025＝0.950.]‎ ‎2．一只蚂蚁位于数轴x＝0处，这只蚂蚁每隔一秒钟向左或向右移动一个单位长度，设它向右移动的概率为，向左移动的概率为，则3秒后，这只蚂蚁在x＝1处的概率为(　　) ‎ ‎【导学号：95032220】‎ A． B． C．1 D． A　[由题意知，3秒内蚂蚁向左移动一个单位长度，向右移动两个单位长度，所以蚂蚁在x＝1处的概率为C××＝.]‎ 二、填空题 ‎3．在一次数学考试中，第14题和第15题为选做题．规定每位考生必须且只需在其中选做一题．设4名考生选做这两题的可能性均为.其中甲、乙2名学生选做同一道题的概率是________．‎ 　[设事件A表示“甲选做第14题”，事件B表示“乙选做第14题”，则甲、乙2名学生选做同一道题的事件为“AB＋ ”，且事件A、B相互独立．‎ 所以P(AB＋)＝P(A)P(B)＋P()P()＝×＋＝.]‎ ‎4．某人参加驾照考试，共考6个科目，假设他通过各科考试的事件是相互独立的，并且概率都是p.若此人未能通过的科目数ξ的均值是2，则p＝________. ‎ ‎【导学号：95032221】‎ 　[因为通过各科考试的概率为p，所以不能通过考试的概率为1－p，易知ξ～B(6,1－p)，所以E(ξ)＝6(1－p)＝2，解得p＝.]‎ 三、解答题 ‎5．在甲、乙等6个单位参加的一次“唱读讲传”演出活动中，每个单位的节目集中安排在一起，若采用抽签的方式随机确定各单位的演出顺序(序号为1,2，…，6)，求：‎ ‎(1)甲、乙两单位的演出序号至少有一个为奇数的概率；‎ ‎(2)甲、乙两单位之间的演出单位个数ξ的分布列与均值．‎ ‎[解]　只考虑甲、乙两单位的相对位置，故可用组合计算基本事件数．‎ 5‎ ‎(1)设A表示“甲、乙的演出序号至少有一个为奇数”，则表示“甲、乙的演出序号均为偶数”，由等可能性事件的概率计算公式得P(A)＝1－P()＝1－＝1－＝.‎ ‎(2)ξ的所有可能取值为0,1,2,3,4，且 P(ξ＝0)＝＝，P(ξ＝1)＝＝，P(ξ＝2)＝＝，P(ξ＝3)＝＝，P(ξ＝4)＝＝.‎ 从而知ξ的分布列为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P 所以E(ξ)＝0×＋1×＋2×＋3×＋4×＝.‎ 5‎