【百强校】甘肃省兰州市第一中学2019届高三最后高考冲刺模拟数学（文）试题 11页

兰州一中2019届高三冲刺模拟试题 数学（文科）‎ 说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟. 请将答案填在答题卡上.‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，‎ 只有一项是符合题目要求的）‎ ‎1. 已知集合A=，则=(　　) ‎ A. （2，6） B. （2，7） C.（-3，2] D.（-3，2）[来源:Zxxk.Com]‎ ‎2. 已知复数，复数满足，则 (　　)‎ A． B． C． D． ‎ ‎3. 已知正项等比数列{an}满足a3＝1，a5与a4的等差中项为，则a1的值为(　　)‎ A. 4 B. 2 C. D. ‎4．已知命题，命题，则(　　)‎ A. 命题是真命题 B. 命题是假命题 C. 命题是假命题 D. 命题是真命题 ‎ ‎5. 设数列{an}满足a1＋2a2＝3，点Pn(n，an)对任意的n∈N*，都有＝(1，2)，则数列{an}的前n项和Sn为(　　)‎ A.n B.n C.n D.n ‎6. 已知函数是上的偶函数，且对任意的有，当 时，，则（ ）‎ A. 11 B. 5 C. -9 D. -1‎ ‎7. 某程序框图如图所示，若该程序运行后输出的值是，则的值是（ ）[来源:Z。xx。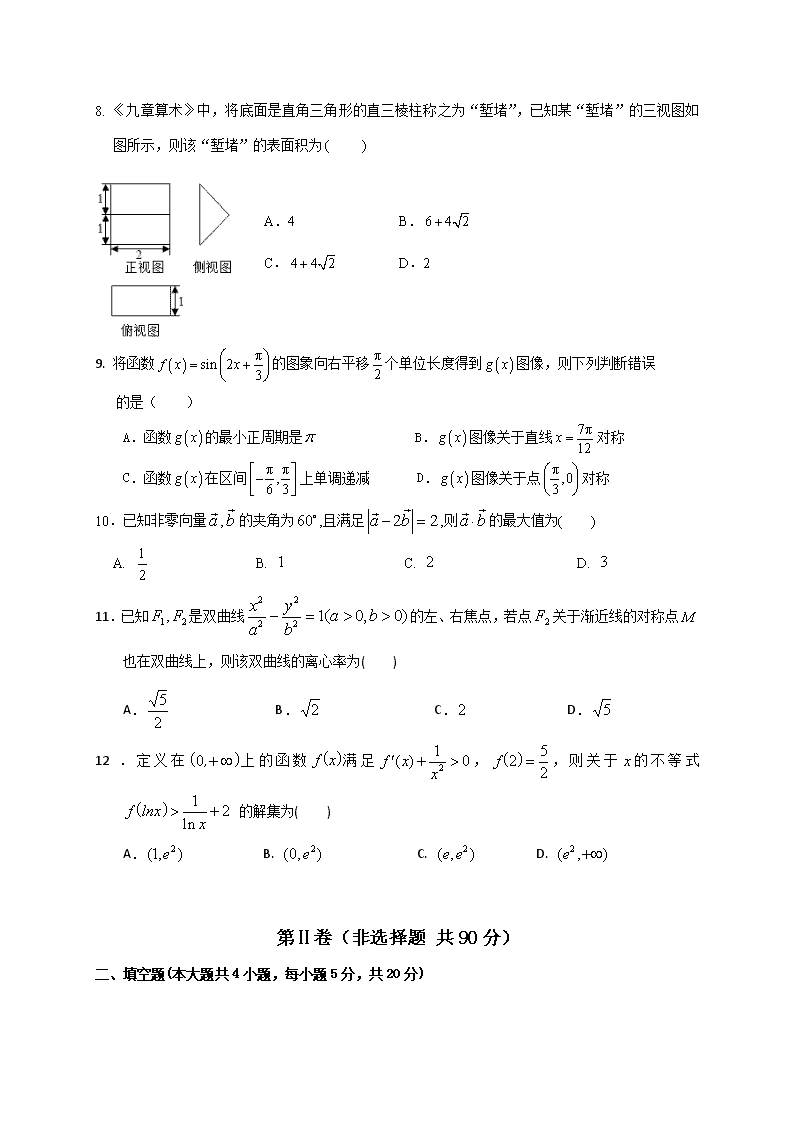k.Com]‎ A．7 B．6 C．5 D．4‎ ‎8. 《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示，则该“堑堵”的表面积为　　‎ A．4 B． ‎ C． D．2‎ ‎[来源:学科网]‎ ‎9. 将函数的图象向右平移个单位长度得到图像，则下列判断错误 的是（ ）‎ A．函数的最小正周期是 B．图像关于直线对称 C．函数在区间上单调递减 D．图像关于点对称 ‎10．已知非零向量,的夹角为,且满足,则的最大值为(　　)‎ A. B. C. D. ‎ ‎11．已知是双曲线的左、右焦点，若点关于渐近线的对称点也在双曲线上，则该双曲线的离心率为(　　)‎ A． B． C． D．‎ ‎12．定义在上的函数满足，，则关于的不等式 的解集为(　　)‎ A． B. C. D. ‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题(本大题共4小题，每小题5分，共20分)‎ ‎13．若满足约束条件的最小值为__________．‎ ‎14．已知A，B，C三点在球O的表面上，AB=BC=CA=2，且球心O到平面ABC的距离等于球半径的，则球O的表面积为 ．‎ ‎15．为了考查考生对于“数学知识形成过程”的掌握情况，某高校自主招生考试面试中的一个问题是：写出对数的换底公式，并加以证明．甲、乙、丙三名考生分别写出了不同的答案．公布他们的答案后，三考生之间有如下对话，甲说：“我答错了”；乙说：“我答对了”；丙说：“乙答错了”．评委看了他们的答案，听了他们之间的对话后说：你们三人的答案中只有一人是正确的，你们三人的对话中只有一人说对了．根据以上信息，面试问题答案正确的考生为 ．‎ ‎16．已知抛物线C：x2＝4y的焦点为F，E为y轴正半轴上的一点．且OE＝3OF（O为坐标原点），若抛物线C上存在一点M（x0，y0），其中x0≠0，使过点M的切线l⊥ME，则切线l在y轴上的截距为　 　．‎ 三、解答题(本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤) ‎ ‎17．（本小题12分）[来源:Z_xx_k.Com]‎ 在中，角的对边分别是.已知.‎ ‎(Ⅰ)求角C；‎ ‎(Ⅱ)若，求的面积.‎ ‎18. (本小题12分）‎ 某商场营销人员进行某商品的市场营销调查时发现，每回馈消费者一定的点数，该商品每天的销量就会发生一定的变化，经过试点统计得到以下表：‎ 反馈点数t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 销量（百件）/天 ‎0.5‎ ‎0.6‎ ‎1‎ ‎1.4‎ ‎1.7‎ ‎（Ⅰ）经分析发现，可用线性回归模型拟合当地该商品销量（千件）与返还点数之间的相关关系.试预测若返回6个点时该商品每天的销量；‎ ‎（Ⅱ）若节日期间营销部对商品进行新一轮调整.已知某地拟购买该商品的消费群体十分庞大，经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查，得到如下一份频数表：‎ 返还点数预期值区间 ‎（百分比）‎ ‎[1,3)‎ ‎[3,5)‎ ‎[5,7)‎ ‎[7,9)‎ ‎[9,11)‎ ‎[11,13)‎ 频数 ‎20‎ ‎60‎ ‎60‎ ‎30‎ ‎20‎ ‎10‎ 将对返点点数的心理预期值在和的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者，现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名，再从这6人中随机抽取3名进行跟踪调查，设抽出的3人中至少有1名“欲望膨胀型”消费者的概率. ‎ ‎19. (本小题12分）‎ 如图，在三棱柱ABC-A1B1C1中，侧棱垂直底面，，， 是棱的中点.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）平面分此棱柱为两部分，求这两部分体积的比．‎ ‎20. (本小题12分) ‎ 椭圆C:(a>b>0)的左、右焦点分别为F1、F2，离心率为，过焦点F2且垂直于x轴的直线被椭圆C截得的线段长为1．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）已知点M（0，-1），直线l经过点N（2，1）且与椭圆C相交于A,B两点（异于 点M），记直线MA的斜率为k1，直线MB的斜率为k2，证明：k1+k2为定值，并求出该定值.‎ ‎21. (本小题12分）‎ 已知函数(,).‎ ‎（Ⅰ）当时，讨论函数的单调性； (Ⅱ) 若函数在（e为自然对数的底）时取得极值，且函数在 ‎ ‎ 上有两个零点，求实数的取值范围.‎ ‎22．(本小题10分)【选修4—4：坐标系与参数方程】‎ 己知直线l的参数方程为 (t为参数)，曲线C的极坐标方程为rsin2q -16cosq=0，直线l与曲线C交于A、B两点，点P(1,3)．‎ ‎(Ⅰ) 求直线l的普通方程和曲线C的直角坐标方程；‎ ‎(Ⅱ) 求的值.‎ ‎23. (本小题10分）【选修4 — 5：不等式选讲】‎ 已知函数f(x)=|2x-1|+|x+1|. ‎ ‎（Ⅰ）解不等式f(x)≥3;‎ ‎（Ⅱ）记函数f(x)的最小值为m，若a,b,c均为正实数，且a+2b+3c=2m，求a2+b2+c2的最 小值.‎ 兰州一中2019届高三冲刺模拟数学（文科）‎ 参考答案 一、选择题: 本大题共12小题，每小题5分，共60分.‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C B A A A C D B C B D D 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13. 5 14. 6π 15. 甲 16. -1‎ 三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. ‎ ‎17．（本小题12分）‎ ‎【解析】(Ⅰ)∵，‎ ‎∴，‎ ‎∴，∴. ‎ ‎∵， ∴. ………………（6分）‎ ‎(Ⅱ)∵，∴，‎ ‎∵，∴，‎ ‎∴. …………………………（12分）‎ ‎18. （本小题12分）‎ ‎【解析】（Ⅰ）易知，‎ 则y关于t的线性回归方程为，‎ 当时，，即返回6个点时该商品每天销量约为2千件. ………………（4分）‎ ‎（Ⅱ）设从“欲望膨胀型”消费者中抽取x人，从“欲望紧缩型”消费者中抽取y人，‎ ‎ 由分层抽样的定义可知，解得 ‎ 在抽取的6人中，2名“欲望膨胀型”消费者分别记为，4名“欲望紧缩型”消费者分别记为 ‎ ，则所有的抽样情况如下：‎ ‎ ‎ ‎ ‎ ‎ ‎ 共20种，其中至少有1名“欲望膨胀型”消费者的情况有16种。记事件A为“抽出的3人中至少有1名‘欲望膨胀型’消费者”，则 ………………（12分）‎ ‎19. （本小题12分）‎ ‎【解析】（Ⅰ）证明：由题设知BC⊥ CC1，BC⊥ AC，CC1∩AC＝C，[来源:Z.xx.k.Com]‎ 所以BC⊥ 平面ACC1A1．‎ 又DC1⊂ 平面ACC1A1，所以DC1⊥ BC．‎ 由题设知∠ A1DC1＝∠ ADC＝45°，‎ 所以∠ CDC1＝90°，即DC1⊥ DC．‎ 又DC∩BC＝C，所以DC1⊥ 平面BDC．‎ 又DC1⊂ 平面BDC1，故平面BDC1⊥ 平面BDC． ………………（6分）‎ ‎（Ⅱ）设棱锥B—DACC1的体积为V1，AC＝1．‎ 由题意得V1＝××1×1＝．‎ 又三棱柱ABC—A1B1C1的体积V＝1，‎ 所以（V－V1）∶V1＝1∶1．‎ 故平面BDC1分此棱柱所得两部分体积的比为1∶1． ………………（12分）‎ ‎20. (本小题12分) ‎ ‎【解析】（Ⅰ）将代入中，由可得，‎ 所以弦长为，………………2分 故有，解得，所以椭圆的方程为：．………（4分） ‎ ‎（Ⅱ）若直线l的斜率不存在，即直线的方程为x=2，与椭圆只有一个交点，不符合题意。‎ 设直线l的斜率为k，若k=0，直线l与椭圆只有一个交点，不符合题意，故k≠0.‎ 所以直线l的方程为，即， 直线l的方程与椭圆的标准方程联立得：‎ 消去y得:,‎ 设，则，‎ ‎,‎ ‎，‎ 把代入上式，得 ‎，命题得证. ………（12分） ‎ ‎21. (本小题12分）‎ ‎【解析】（Ⅰ）当时，，‎ ‎，令，得，‎ 当时，，当时，.‎ 所以函数在上单调递增，在上单调递减. …………………(4分)‎ ‎（Ⅱ），，‎ ‎∵在时取得极值，‎ ‎∴即，∴.‎ 所以，，‎ 函数在上单调递增，在上单调递减，‎ 得函数的极大值，‎ ‎∴当函数在上有两个零点时，必有 ,得.‎ 当时，.‎ ‎∴的两个零点分别在区间与中.‎ ‎∴的取值范围是. …………………(12分)‎ ‎22．(本小题10分)【选修4—4：坐标系与参数方程】‎ ‎【解析】（Ⅰ）直线l的普通方程y=2x+1………………………..（2分）‎ ‎ 曲线C的直角坐标方程y2=16x …………………………….（5分）‎ ‎（Ⅱ）直线的参数方程改写为代入.‎ ‎ ，…………….（8分）‎ ‎ ……………………………….（10分） ‎ ‎23. (本小题10分）【选修4 — 5：不等式选讲】‎ ‎【解析】（Ⅰ）f(x)= ‎ 解得：x≤-1，或x≥1， 所以不等式的解集为{x|x≤-1，或x≥1}. …………………（5分）‎ ‎（Ⅱ）由(1)可知,当x=时,f(x)取得最小值, ‎ 所以m=,即a+2b+3c=3,‎ 由柯西不等式得(a2+b2+c2 )(12+22+32)≥(a+2b+3c)2=9,‎ 整理得a2+b2+c2≥,‎ 当且仅当时, 即时等号成立.‎ 所以a2+b2+c2的最小值为. …………………（10分）‎