2015年普通高等学校招生全国统一考试 理科数学（北京卷） 11页

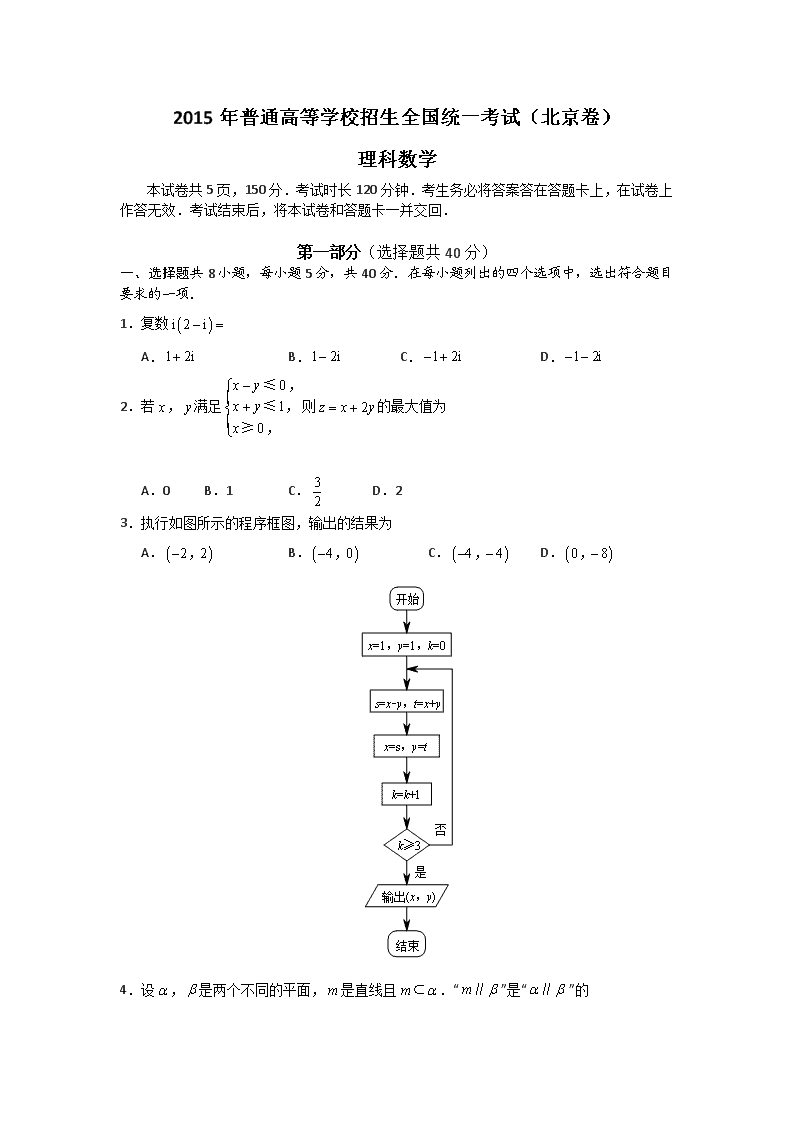
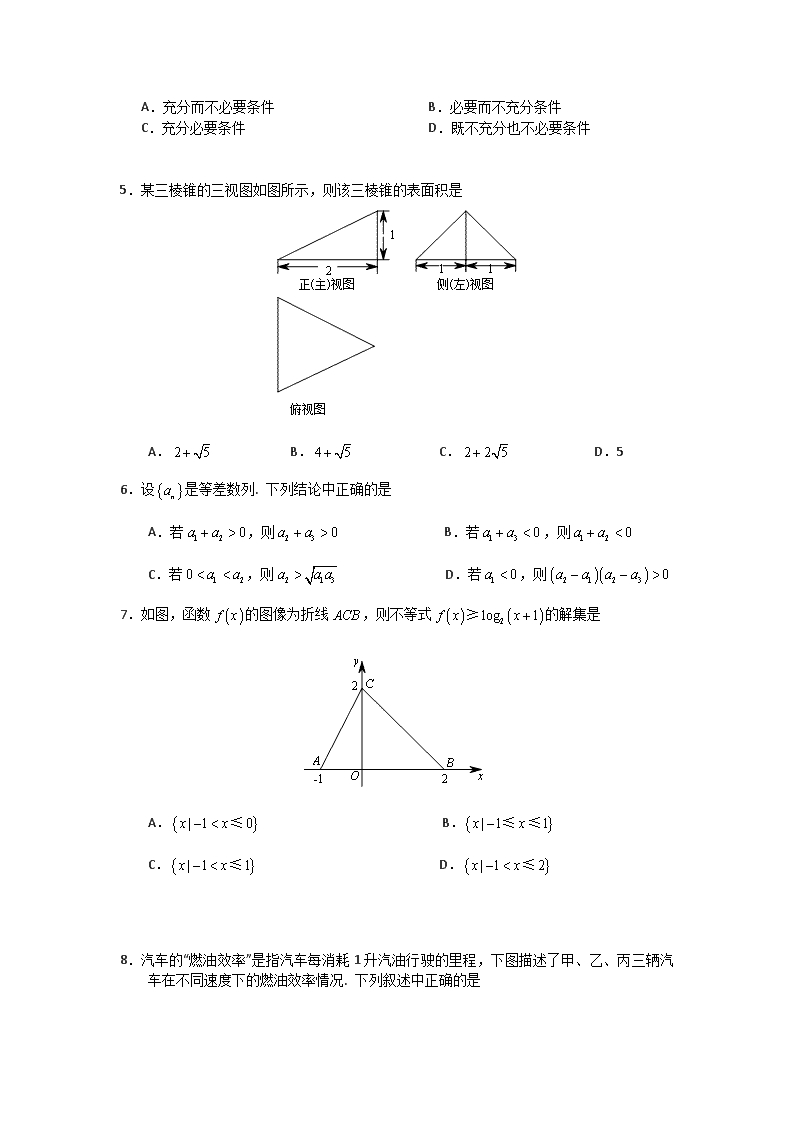
‎2015年普通高等学校招生全国统一考试（北京卷）‎ 理科数学 本试卷共5页，150分．考试时长120分钟．考生务必将答案答在答题卡上，在试卷上作答无效．考试结束后，将本试卷和答题卡一并交回．‎ 第一部分（选择题共40分）‎ 一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．‎ ‎1．复数 A． B． C． D．‎ ‎2．若，满足则的最大值为 A．0 B．1 C． D．2 ‎ ‎3．执行如图所示的程序框图，输出的结果为 A． B． C． D．‎ ‎4．设，是两个不同的平面，是直线且．“”是“”的 A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎5．某三棱锥的三视图如图所示，则该三棱锥的表面积是 A． B． C． D．5‎ ‎6．设是等差数列. 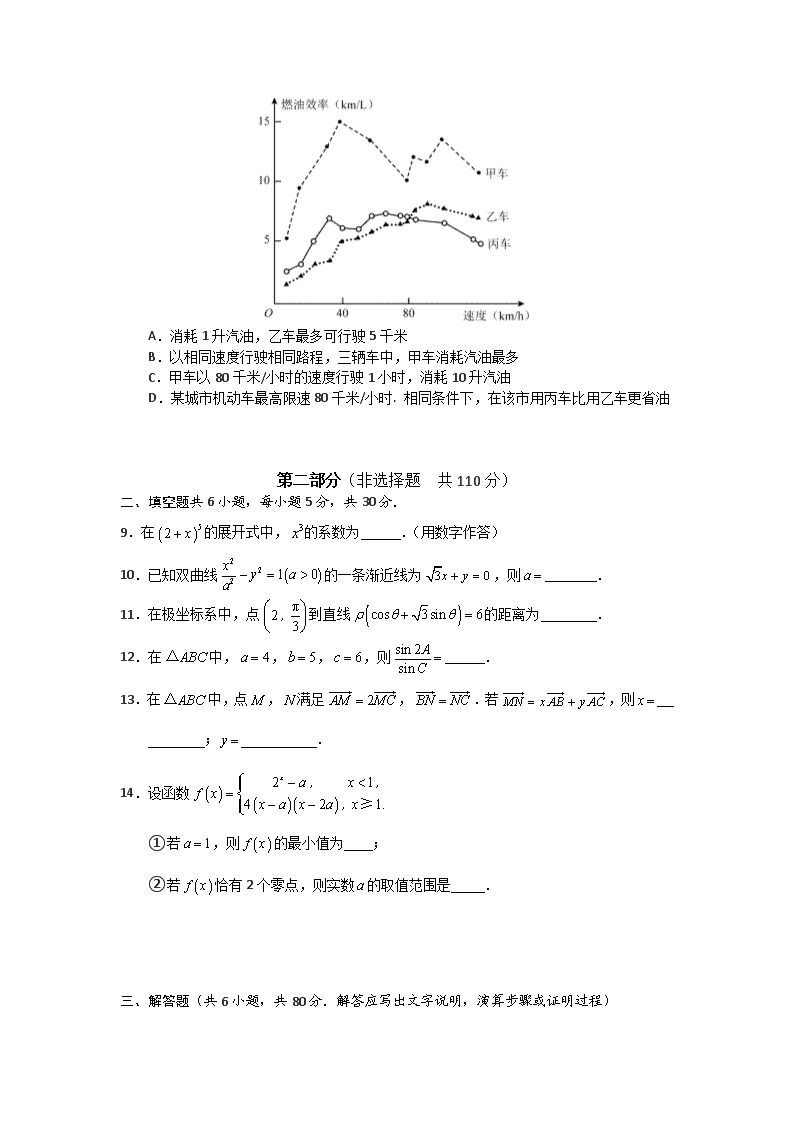下列结论中正确的是 A．若，则 B．若，则 C．若，则 D．若，则 ‎7．如图，函数的图像为折线，则不等式的解集是 A． B．‎ C． D．‎ ‎8．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是 A．消耗1升汽油，乙车最多可行驶5千米 B．以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多 C．甲车以80千米/小时的速度行驶1小时，消耗10升汽油 D．某城市机动车最高限速80千米/小时. 相同条件下，在该市用丙车比用乙车更省油 第二部分（非选择题　共110分）‎ 二、填空题共6小题，每小题5分，共30分．‎ ‎9．在的展开式中，的系数为 ．（用数字作答）‎ ‎10．已知双曲线的一条渐近线为，则 ．‎ ‎11．在极坐标系中，点到直线的距离为 ．‎ ‎12．在中，，，，则 ．‎ ‎13．在中，点，满足，．若，则 ； ．‎ ‎14．设函数 ‎ ①若，则的最小值为 ；‎ ‎②若恰有2个零点，则实数的取值范围是 ．‎ 三、解答题（共6小题，共80分．解答应写出文字说明，演算步骤或证明过程）‎ ‎15．（本小题13分）‎ 已知函数．‎ ‎(Ⅰ) 求的最小正周期；‎ ‎(Ⅱ) 求在区间上的最小值．‎ ‎16．（本小题13分）‎ ‎，两组各有7位病人，他们服用某种药物后的康复时间（单位：天）记录如下：‎ 组：10，11，12，13，14，15，16‎ 组：12，13，15，16，17，14，‎ 假设所有病人的康复时间互相独立，从，两组随机各选1人，组选出的人记为甲，组选出的人记为乙．‎ ‎(Ⅰ) 求甲的康复时间不少于14天的概率；‎ ‎(Ⅱ) 如果，求甲的康复时间比乙的康复时间长的概率；‎ ‎(Ⅲ) 当为何值时，，两组病人康复时间的方差相等？（结论不要求证明）‎ ‎17．（本小题14分）‎ 如图，在四棱锥中，为等边三角形，平面平面，，，，，为的中点．‎ ‎(Ⅰ) 求证：；‎ ‎(Ⅱ) 求二面角的余弦值；‎ ‎(Ⅲ) 若平面，求的值．‎ ‎18．（本小题13分）‎ ‎ 已知函数．‎ ‎ （Ⅰ）求曲线在点处的切线方程；‎ ‎（Ⅱ）求证：当时，；‎ ‎（Ⅲ）设实数使得对恒成立，求的最大值．‎ ‎19．（本小题14分）‎ 已知椭圆：的离心率为，点和点都在椭圆上，直线交轴于点．‎ ‎（Ⅰ）求椭圆的方程，并求点的坐标（用，表示）；‎ ‎（Ⅱ）设为原点，点与点关于轴对称，直线交轴于点．问：轴上是否存在点，使得？若存在，求点的坐标；若不存在，说明理由．‎ ‎20．（本小题13分）‎ 已知数列满足：，，且．‎ 记集合．‎ ‎（Ⅰ）若，写出集合的所有元素；‎ ‎（Ⅱ）若集合存在一个元素是3的倍数，证明：的所有元素都是3的倍数；‎ ‎（Ⅲ）求集合的元素个数的最大值．‎ ‎（考生务必将答案答在答题卡上，在试卷上作答无效）‎ ‎2015年普通高等学校招生全国统一考试（北京卷）‎ 理科数学答案 一、选择题（共8小题，每小题5分，共40分）‎ ‎（1）A (2)D（3）B（4）B（5）C（6）C（7）C（8）D 二、填空题（共6小题，每小题5分，共30分）‎ ‎（9）40 （10） （11）1 （12）1 （13） （14）1，≤ a <1 或a ≥ 2‎ 三、解答题（共6小题，共80分）‎ ‎（15）（共13分）‎ 解：（I）因为 ‎ 所以的最小正周期为2‎ ‎（Ⅱ）因为，所以 当，即时，取得最小值。‎ 所以在区间上的最小值为 ‎（16）（本小题13分）‎ 解：设时间为“甲是A组的第i个人”，‎ 时间为“乙是B组的第i个人”，i=1,2，…，7.‎ 由题意可知, i=1,2，…，7.‎ ‎（Ⅰ）由题意知，时间“甲的康复时间不少于14天”等价于“甲是A组的第5人，或者第6人，或者第7人”，所以甲的康复时间不少于14天的概率是 ‎（Ⅱ）设时间C为“甲的康复时间比乙的康复时间长”.由题意知，‎ C=.‎ 因此 ‎ ‎ ‎ =10‎ ‎ =10‎ ‎ =‎ ‎（Ⅲ）a=11或a=18‎ ‎（17）（本小题14分） ‎ 解：（I）因为△AEF是等边三角形，O为EF的中点，‎ 所以AO⊥EF.‎ ‎ 又因为平面AEF⊥平面EFCB，AO平面AEF，‎ 所以AO⊥平面EFCB.‎ ‎ 所以AO⊥BE. （Ⅱ）取BC中点G，连接OG.‎ ‎ 由题设知EFCB是等腰梯形，‎ ‎ 所以OG⊥EF. ‎ ‎ 由（I）知AO⊥平面EFCB ‎ 又OG平面EFCB，‎ ‎ 所以OA⊥OG.‎ ‎ 如图建立空间直角坐标系O-xyz，‎ ‎ 则E（a,0,0），A（0，0，），‎ ‎ B（2，（2-a），0），=（-a，0，），‎ ‎ =（a-2，（a-2）,0）.‎ ‎ 设平面ABE的法向量为n=（x,y,z）‎ ‎ 则： 即 ‎ 令z=1，则x=，y=-1.于是n=（，-1,1）‎ ‎ 平面AEF是法向量为p=（0,1,0）‎ ‎ 所以cos（n，p）==.‎ ‎ 由题知二维角F-AE-B为钝角，所以它的余弦值为 ‎ （Ⅲ）因为BE⊥平面AOC，所以BE⊥OC，即.‎ ‎ 因为=（a-2 ，（a-2），0），=（-2，（2-a），0），‎ ‎ 所以=-2（a-2）-3.‎ ‎ 由及00（0=0，x∈（0，1），‎ ‎ 即当x∈（0，1）时，>2(x+).‎ ‎（Ⅲ）由（Ⅱ）知，当k《2时，>k(x+)对x∈（0，1）恒成立.‎ ‎ 当k>2时，令=- k(x+)，则 ‎ =-k（1+）=.‎ ‎ 所以当时，<0，因此在区间（0，）上单调递减.‎ ‎ 当时，<=0，即< k(x+).‎ ‎ 所以当K>2时，> k(x+)并非对x∈（0，1）恒成立.‎ ‎ 综上可知，k的最大值为2。‎ ‎（19）（本小题14分）‎ 解：（Ⅰ）由题意得解得=2.‎ 故椭圆C的方程为 设M（，0）.‎ 因为m≠0，所以-11，因为=2或=2-36，所以2是3的倍数，于是是3的倍数，；类似可得，，…，都是3的倍数，从而对任意，是3的倍数，因此M的所有元素都是3的倍数.‎ ‎ 综上，若集合M存在一个元素是3的倍数，则M的所有元素都是3的倍数.‎ ‎（Ⅲ）由，可归纳证明.‎ ‎ 由于是正整数，所以是2的倍数.‎ 从而当时，是4的倍数.‎ ‎ 如果是3的倍数，由（Ⅱ）知对所有正整数n，是3的倍数.‎ ‎ 因此当时，.这时M的元素个数不超过5.‎ ‎ 如果不是3的倍数，由（Ⅱ）知所有正整数n，不是3的倍数.‎ ‎ 因此当时.这时M的元素个数不超过8.‎ ‎ 当=1时，有8个元素.‎ ‎ 综上可知，集合M的元素个数最大值为8.‎