2018_2019学年七年级数学下册第9章平行线9-3平行线的性质教学课件（新版）青岛版 19页

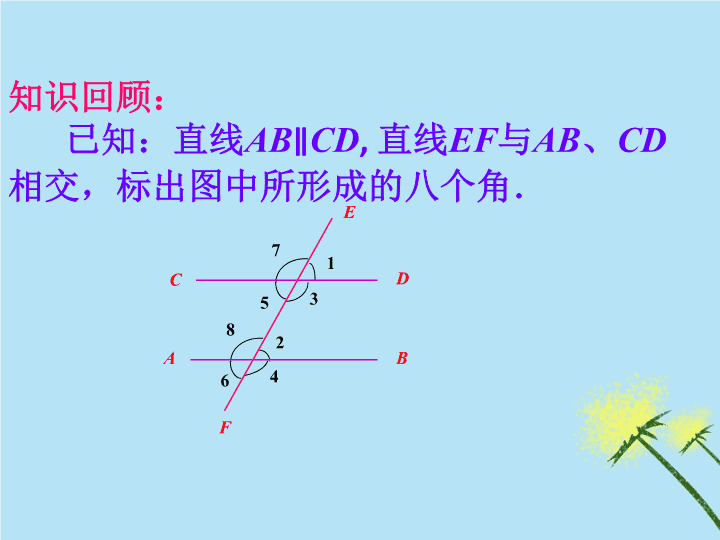
教学课件数学七年级下册青岛版 第9章平行线9.3平行线的性质 知识回顾：已知：直线AB∥CD,直线EF与AB、CD相交，标出图中所形成的八个角．3ABCDEF1245678 请你猜想一下∠1与∠2的数量关系。ABCDEF12456783∠1与∠2是什么角？（同位角，内错角，同旁内角） 两直线平行的性质(1):EBACDF12两条直线被第三条直线所截，如果两直线平行,那么同位角相等.书写格式:∵AB∥CD∴∠1=∠2(已知)(两直线平行，同位角相等) EBACDF125已知：AB∥CD你能猜想出∠2和∠5有什么关系吗？试证明之。∵AB∥CD(已知)∴∠1=∠2(两直线平行,同位角相等).又∵∠1=∠5(对顶角相等)∴∠2=∠5(等量代换).证明： 两直线平行的性质(2)B52ADEF两条直线被第三条直线所截，如果两直线平行,那么内错角相等.书写格式:∵AB∥CD∴∠2=∠5(已知)(两直线平行，内错角相等)C EBACDF123已知：AB∥CD你能猜想出∠2和∠3有什么关系吗？试证明之。∵AB∥CD(已知)∴∠1=∠2(两直线平行,同位角相等).又∵∠1+∠3=180°(等量代换)证明：（邻补角定义）∴∠2+∠3=180° 两直线平行的性质(3):2BACDEF3两条直线被第三条直线所截，如果两直线平行,那么同旁内角互补.书写格式:∵AB∥CD∴∠2+∠3=180°(已知)(两直线平行，同旁内角互补) 平行线的性质：1、两直线平行,同位角相等2、两直线平行,内错角相等3、两直线平行,同旁内角互补. 如图,已知平行线AB,CD被直线AE所截.2431ABCDE⑴∵AB∥CD（两直线平行,内错角相等）⑵∵AB∥CD(两直线平行,同位角相等)例1解：∴∠2=∠1=110°∴∠3=∠1=110°∴∠1+∠4=180°∴∠4=（两直线平行，同旁内角互补）（等式的性质）（已知）（已知）（已知）⑶∵AB∥CD=70° 例2如图,CD平分∠ACB,DE∥AC,且∠1=35°,求∠2的度数.∵CD平分∠ACB,∠1=35°∵DE∥AC（已知）（两直线平行,同位角相等）（已知）解：（角平分线的定义）分析：DE∥ACCD平分∠ACB 练习1．如图梯子的各条横档互相平行，∠1=100°,求∠2的度数。123ABCD解：∵DC∥AB∴∠3=∠1=100°（两直线平行,同位角相等）又∵∠2+∠3=180°∴∠2=（已知）（邻补角定义）分析：∠3=∠1DC∥AB（等式的性质）=80° 练习2.如图,已知:DE∥CB,∠1=∠2求证:CD平分∠ECB.∵DE∥CB（已知）（两直线平行,内错角相等）（已知）(等量代换)证明：分析：即：CD平分∠ECB.DE∥CB 练习3：如图是梯形有上底的部分，其中AC∥BD已量得∠A=115°，∠D=100°，求梯形另外两个角各是多少度？∵AC∥BD（两直线平行，同旁内角互补）（已知）你能类似的说出∠C的度数吗？分析：AC∥BD解：（等式的性质）=65° 练习4、如图,若AD∥BC,则∠______=∠_______,∠_______=∠_______,∠ABC+∠_______=180°;(2)若DC∥AB,则　∠______=∠_______,∠_______=∠_________,∠ABC+∠________=180°. 练习5.一个人驱车前进时,两次拐弯后,按原来的相反方向前进,这两次拐弯的角度是()A.向右拐85°,再向右拐95°；B.向右拐85°,再向左拐85°；C.向右拐85°,再向右拐85°；D.向右拐85°,再向左拐95°.练习6.如图,已知:DE∥CB,∠1=∠2,求证:CD平分∠ECB.BCDE 这节课你学会了什么？ 平行线有哪些性质？1、两直线平行,同位角相等2、两直线平行,内错角相等3、两直线平行,同旁内角互补.