七年级下数学课件《平行线的性质》课件2_冀教版 9页

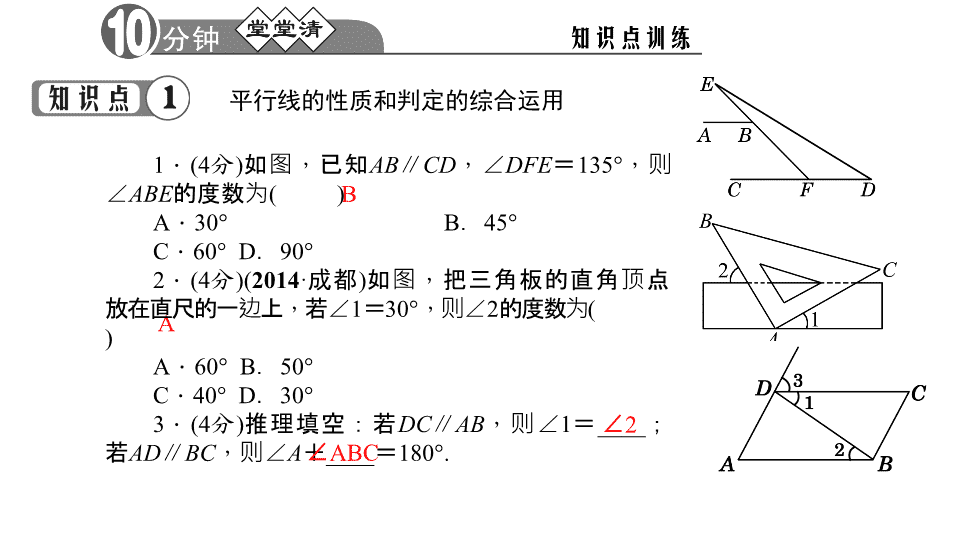
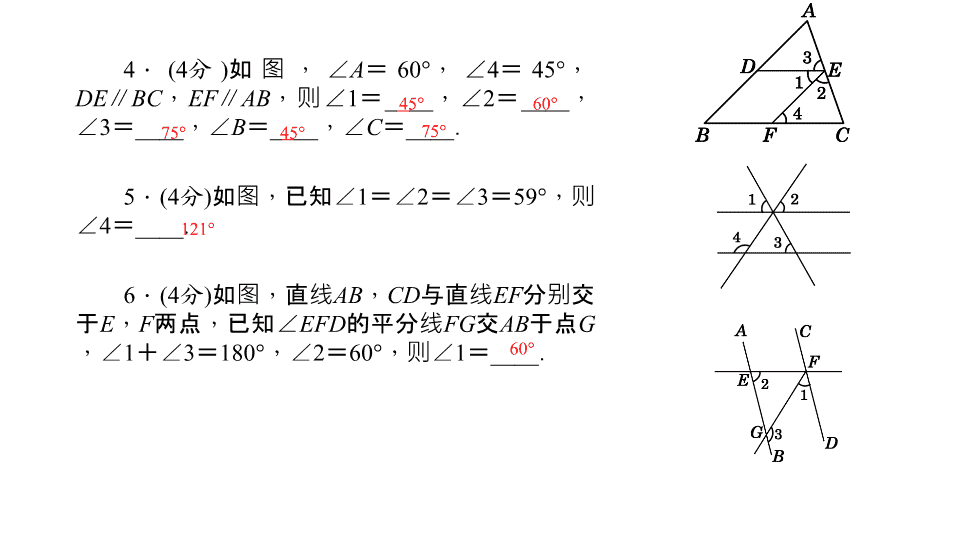
第2课时　平行线的性质和判定的综合运用得分________卷后分________评价________相等相等互补1．平行线的判定定理：同位角____，两直线平行；内错角_，两直线平行；同旁内角____，两直线平行．2．平行线的性质定理：两直线平行，同位角____；两直线平行，内错角____；两直线平行，同旁内角____．3．平行于同一条直线的两条直线____．相等相等互补平行 BA平行线的性质和判定的综合运用1．(4分)如图，已知AB∥CD，∠DFE＝135°，则∠ABE的度数为()A．30°B．45°C．60°D．90°2．(4分)(2014·成都)如图，把三角板的直角顶点放在直尺的一边上，若∠1＝30°，则∠2的度数为()A．60°B．50°C．40°D．30°3．(4分)推理填空：若DC∥AB，则∠1＝____；若AD∥BC，则∠A＋____＝180°.∠2∠ABC 4．(4分)如图，∠A＝60°，∠4＝45°，DE∥BC，EF∥AB，则∠1＝____，∠2＝____，∠3＝____，∠B＝____，∠C＝____．5．(4分)如图，已知∠1＝∠2＝∠3＝59°，则∠4＝____.6．(4分)如图，直线AB，CD与直线EF分别交于E，F两点，已知∠EFD的平分线FG交AB于点G，∠1＋∠3＝180°，∠2＝60°，则∠1＝____．45°60°75°45°75°121°60° 平行于同一条直线的两条直线平行过直线外一点有且只有一条直线与这条直线平行平行于同一条直线的两条直线互相平行平行于同一条直线的两条直线平行7．(4分)如图①和②，在每一步推理后面的括号内填上理由．(1)∵AB∥CD，EF∥CD，∴AB∥EF()．(2)∵AB∥CD，过点F画EF∥AB()．∴EF∥CD()．8．(4分)已知三直线a1，a2，a3，若a1⊥a3，a2∥a3，则a1与a2的关系是()A．a1∥a2B．a1⊥a2C．a1与a2重合D．a1与a2斜交B 9．(8分)如图，直线a∥b，b∥c，d与a相交于点M.(1)试判断直线a，c的位置关系，并说明理由．(2)判断c与d的位置关系，并说明理由．解：(1)平行，理由略(2)相交，理由略 BDC一、选择题(每小题4分，共20分)10．(2014·山西)如图，直线AB，CD被直线EF所截，AB∥CD，∠1＝110°，则∠2等于()A．65°B．70°C．75°D．80°11．(2014·丽水)如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1＝60°，则∠2的度数是()A．50°B．45°C．35°D．30°12．如图所示，AB∥CD∥EF，∠ABE＝28°，∠DCE＝140°，则∠BEC等于()A．28°B．40°C．12°D．14° 13．如图所示，AB∥CD，∠C＝40°，∠A＝25°，那么∠E的度数是()A．40°B．50°C．15°D．65°14．如图所示，AB∥CD∥EF，则∠BAD＋∠ADE＋∠DEF等于()A．180°B．270°C．360°D．540°二、填空题(每小题4分，共8分)15．一大门的栏杆如图所示，BA垂直地面AE于点A，CD平行于地面AE，则∠ABC＋∠BCD＝____.16．两平行线中内错角的角平分线的位置关系是____．CC270°平行 三、解答题(共32分)17．(8分)如图所示，在△ABC中，EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD的度数．解：110°18．(8分)如图所示，已知点E在直线DF上，点B在直线AC上，若∠AGB＝∠EHF，∠C＝∠D，则∠A与∠F相等吗？为什么？解：∠A＝∠F，理由如下：∵∠EHF＝∠AHC，∠AGB＝∠EHF，∴∠AHC＝∠AGB.∴BD∥EC.∴∠DBA＝∠C.∵∠C＝∠D，∴∠D＝∠DBA.∴AC∥DF.∴∠A＝∠F 19．(8分)如图所示，已知点D在AB上，DF∥BC，BF平分∠ABC，DE平分∠ADF.问DE和BF平行吗？为什么？解：DE∥BF，∵DF∥BC，∴∠ADE＝∠ABC，又∵BF平分∠ABC，∴∠3＝∠4，DE平分∠ADF.∴∠1＝∠2，∴∠1＝∠3，∴DE∥BF【综合运用】20．(8分)如图所示，∠1＋∠2＝180°，∠3＝∠B，试判断∠AED与∠C的大小关系，并说明你的理由．解：∠AED＝∠C.理由如下，∵∠1＋∠2＝180°，∠1＋∠4＝180°，∴∠2＝∠4.∴AB∥EF.∴∠3＝∠ADE.∵∠3＝∠B，∴∠ADE＝∠B.∴DE∥BC.∴∠AED＝∠C