七年级下数学课件：6-1 平方根 （共22张PPT)_人教新课标 22页

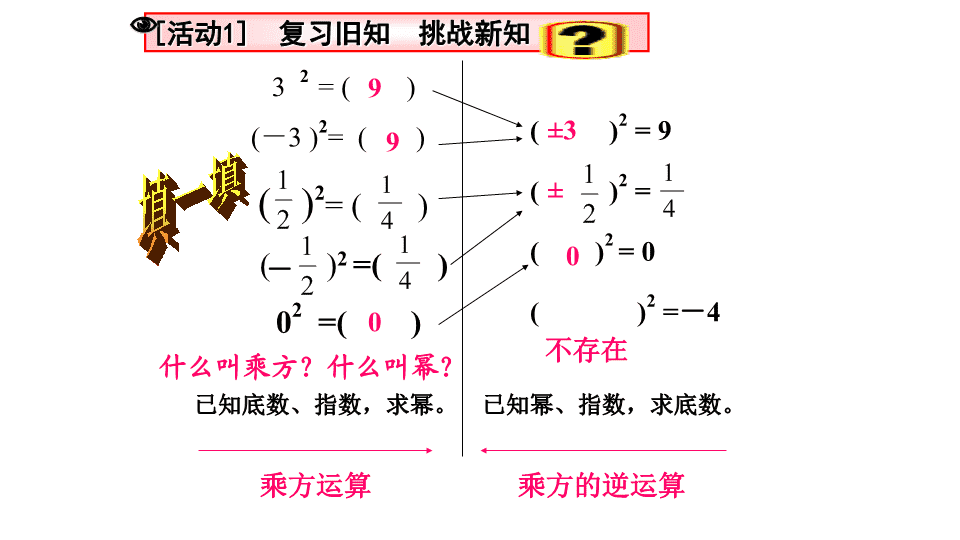
平方根 ±0.8±25±3x211636495x425±4±1±6±7±25？已知X2=a，求这个数X是多少？[活动1]复习旧知挑战新知 已知底数、指数，求幂。已知幂、指数，求底数。()2=9()2=()2=0()2=－432=()(－3)2=()()2=()()2=()02=()990±3－±0不存在乘方运算乘方的逆运算什么叫乘方？什么叫幂？[活动1]复习旧知挑战新知填一填 a是x的二次幂，x是a的平方根(或二次方根)。X2底数指数幂=a如果一个数X的平方等于a，即X2=a，那么这个数X叫做a的平方根（二次方根）[活动2]探究思考内化新知 如果一个数X的平方等于a，即X2=a，那么这个数X叫做a的平方根（二次方根）a的平方根表示为x2=a符号表示求数a的平方根的运算叫做开平方 得出：()2=9()2=()2=0()2=－432=()(－3)2=()()2=()()2=()02=()990±3－±0不存在请同学们概括一个数的平方根的性质：一个正数有两个平方根，它们互为相反数；零有一个平方根，它是零本身；负数没有平方根。 正数有2个平方根，它们互为相反数；0的平方根是0；负数没有平方根。a的一个平方根是3，则另一个平方根是，a=。-393a-22和2a-3是m的两个平方根，试求m的值。 开平方：求一个数a(a≥0)的平方根的运算，叫做开平方，开平方运算是已知指数和幂，求底数。是不是所有的数都能进行开平方运算？不是，只有正数和零才能进行开平方运算。由于平方与开平方互为逆运算，因此可以通过开平方运算来求一个数的平方根，也可以通过平方运算来检验一个数是不是另一个数的平方根。 1、检验下面各题中前面的数是不是后面的数的平方根。（1）±12,144（2）±0.2,0.042、选择题（1）0.01的平方根是（）（A）0.1（B）±0.1（C）0.0001（D）±0.0001（2）∵（0.3）2=0.09∴（）（A）0.09是0.3的平方根.（B）0.09是0.3的3倍.（C）0.3是0.09的平方根.（D）0.3不是0.09的平方根.是是BC[活动3]变式训练巩固新知题组一 3.判断下列说法是否正确：（1）－9的平方根是－3;()（2）49的平方根是7；()（3）（－2）2的平方根是±2；（）（4）7是(-7)2的算术平方根；（）（5）－1是1的平方根;（）（6）7的平方根是±49.()（7）若X2=16则X=4（）(8)的平方根是±14()××√√√××× 4、判断下列说法是否正确：（1）5是25的算术平方根（2）5/6是25/36的一个平方根（3）（－4）2的平方根是－4（4）0的平方根与算术平方根都是0（√）（×）（√）（√）5.问：3有没有平方根？若有，怎样表示？没有，说明为什么？ 学以致用例1求下列各数的平方根：(1)100；(3)0.25(4)(-2005)2(5)11（5）11的平方根是解:(1)∵(±10)2=100,∴100的平方根是±10,100±=±10即(2)∵(±)2=,∴的平方根是±3434=±即±(3)∵(±0.5)2=0.25,∴0.25的平方根是±0.5,即±=0.5(4)∵(±2005)2=(-2005)2,∴(-2005)2的平方根是±2005,即±=±2005 判断下列各数有没有平方根，若有，求其平方根。若没有，说明为什么。（1）0.81（2)（3）（4）（－2）2（5）9（6）0（7）－100（8）102（1）∵∴0.81的平方根是0.9,即（2）∵　　　　　∴　的平方根是，即（7）∵－100是负数，∴－100没有平方根；解：学以致用 例3,已知有意义,求x的取值范围.例2,求下列各式的值:(1);(2)－;(3)±(4)(5) 2.计算下列各式的值：1.如果一个正数的平方根是a-1和a+3,则a=____那么这个正数是＿＿＿4-1[活动3]变式训练巩固新知题组二 3、填空±5550.6-114、填空 5.想一想a2=-a（a<0） 1.一个正数有＿＿个平方根，它们互为＿＿＿＿若一个数只有一个平方根，则这个数为＿＿＿，它的平方根是＿＿＿。2.正数x的平方是＿＿＿，正数x的平方根是＿＿＿平方根是＿＿＿；1.21的平方根是＿＿＿；的平方根是＿＿＿＿2相反数00x2x±1.1±54.（－9）2的平方根是＿＿＿＿＿±95.如果某数的一个平方根是3，则另一个平方根是＿＿＿＿-3[活动3]变式训练巩固新知 [活动3]变式训练巩固新知题组一解：（3）±=±64-11+11-0.6+0.6 [活动3]变式训练巩固新知解:面积为A的正方形的边长为A 体会.分享对自己说,你有什么收获?对老师说,你有什么疑惑?对同学说,你有什么温馨提示?畅所欲言哦[活动４]归纳小结，强化新知 同学们再见！开新每一天！快乐每一天！收获每一天！数学伴我成长！