七年级下册数学课件《整式的除法 单项式除以单项式》 (8)_北师大版 10页

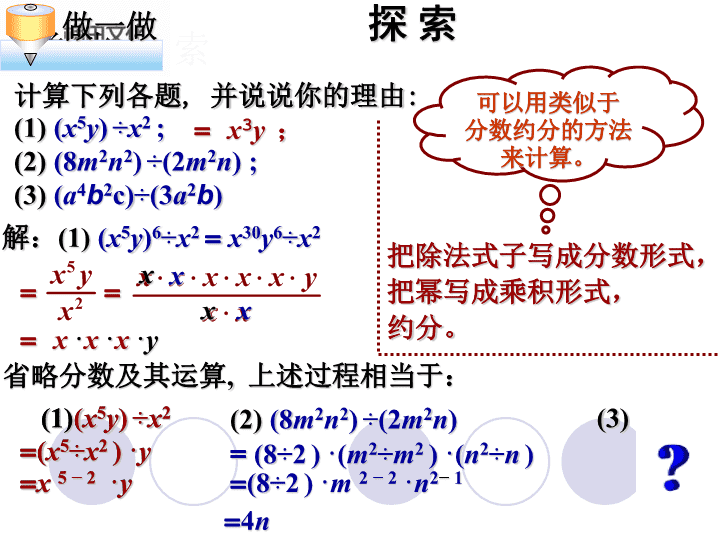
第一章整式的运算整式的除法（1）1.7 回顾与思考回顾&思考☞（a≠0）1、用字母表示幂的运算性质：nma.(3)=;(5)=;(4)=.;(6)=..(1)=;(2)=;12、计算：(1)a20÷a10；(2)a2n÷an(3)(−c)4÷(−c)2；(4)(a2)3·(-a3)÷(a3)5；(5)(x4)6÷(x6)2·(-x4)2。=a10=an=c2=−a9÷a15=−a−6=−=x24÷x12·x8=x24—12+8=x20 类比探索做一做计算下列各题,并说说你的理由:(1)(x5y)÷x2;(2)(8m2n2)÷(2m2n);(3)(a4b2c)÷(3a2b)解：(1)(x5y)6÷x2=x30y6÷x2把除法式子写成分数形式，=把幂写成乘积形式，约分。==x·x·x·yxxxx=x3y；省略分数及其运算,上述过程相当于：(1)(x5y)÷x2=(x5÷x2)·y=x5−2·y可以用类似于分数约分的方法来计算。(2)(8m2n2)÷(2m2n)==(8÷2)·m2−2·n2−1(3)(8÷2)·(m2÷m2)·(n2÷n)探索(1)(x5y)÷x2=(x5÷x2)·y=x5−2·y=4n 观察、归纳观察&归纳(1)(x5y)÷x2=x5−2·y(2)(8m2n2)÷(2m2n)=(8÷2)·m2−2·n2−1;(3)(a4b2c)÷(3a2b)=(1÷3)·a4−2·b2−1·c.商式被除式除式仔细观察一下，并分析与思考下列几点：(被除式的指数)—(除式的指数)(被除式的系数)÷(除式的系数)商式的系数＝单项式除以单项式，其结果(商式)仍是(同底数幂)商的指数＝一个单项式;写在商里面作被除式里单独有的幂，因式。 单项式的除法法则如何进行单项式除以单项式的运算?议一议单项式相除,把系数、同底数的幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连它的指数一起作为商的一个因式。理解商式＝系数•同底的幂•被除式里单独有的幂底数不变，指数相减。保留在商里作为因式。 例题解析例题学一学例1计算：(1);(2)(10a4b3c2)÷(5a3bc);(−x2y3)÷(3x2y3)(1)(2)小题的结构一样,说说可能用到的有关幂的运算公式或法则.观察&思考am÷an=am−n同底幂的除法法则:☾(3)(2x2y)3·(−7xy2)÷(14x4y3);(4)(2a+b)4÷(2a+b)2.[(−7)÷14]·x1−4y2−3题(3)能这样解吗?(2x2y)3·(−7xy2)÷(14x4y3)=(2x2y)3·三块之间是同级运算,只能从左到右.☞括号内是积、括号外右角有指数时，先用积的乘方法则。p40例1(3)解阅读例1(1)(2)阅读(2a+b)4÷(2a+b)2=(24a4b4)÷(22a2b2)题(4)能这样解吗?两个底数是相同的多项式时,应看成一个整体(如一个字母). 随堂练习随堂练习p29(1)(2a6b3)÷(a3b2);(2);(3)(3m2n3)÷(mn)2;(4)(2x2y)3÷(6x3y2).1、计算：(x3y2)÷(x2y)接综合练习 答:月球距离地球大约3.84×105千米,一架飞机的速度约为8×102千米/时.如果乘坐此飞机飞行这么远的距离,大约需要多少时间?3.84×105÷(8×102)？这样列式的依据=0.48×103？如何得到的？单位是什么=480(小时)？如何得到的=20(天).？做完了吗如果乘坐此飞机飞行这么远的距离,大约需要20天时间.解题后的反思你能直接列出一个时间为天的算式吗?3.84×105÷(8×102)÷12.你会计算吗?阅读思考☞解:学以致用学以致用 本节课你的收获是什么？小结本节课你学到了什么?在计算题时，要注意运算顺序和符号．同底数幂相除是单项式除法的特例；单项式除以单项式的法则的探求过程中我们使用了观察、归纳的方法，这是数学发现规律的一种常用方法。 巩固练习1、计算填空:⑴(60x3y5)÷(−12xy3)=;◣◢综(2)(8x6y4z)÷()=−4x2y2;(3)()÷(2x3y3)=;合(4)若(ax3my12)÷(3x3y2n)=4x6y8,则a=,m=,n=;2、能力挑战:−5x2y2−2x4y2z1232