七年级下册数学课件《平行线的特征 平行线的特征探究》 (2)_北师大版 14页

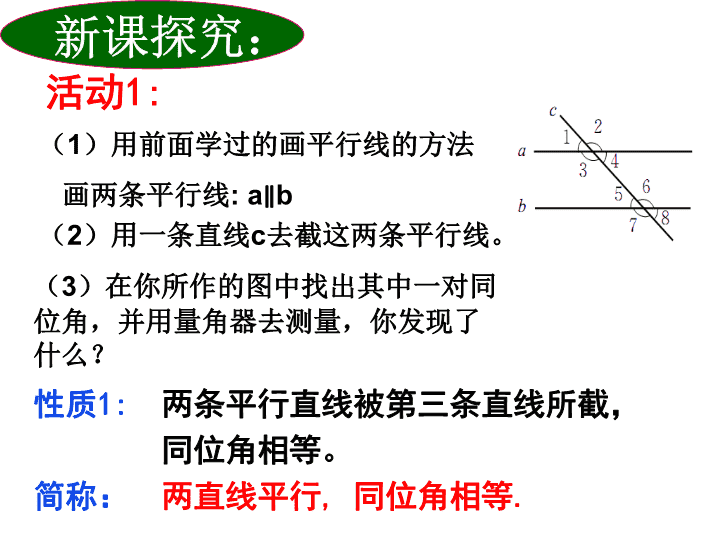
第二章相交线与平行线3.平行线的特征（第1课时） 第一环节：复习回顾，逆向猜想（1)∵∠1=∠5(已知)∴a∥b（____）（2)∵∠4=∠(已知)∴a∥b（内错角相等，两直线平行）（3）∵∠4+∠=1800(已知)∴a∥b（）同位角相等，两直线平行56同旁内角互补，两直线平行 新课探究：（1）用前面学过的画平行线的方法画两条平行线:a∥b（3）在你所作的图中找出其中一对同位角，并用量角器去测量，你发现了什么？活动1:（2）用一条直线c去截这两条平行线。性质1:两条平行直线被第三条直线所截，同位角相等。简称：两直线平行,同位角相等. 解：∠4=∠5理由：∵a∥b(已知）∴∠1=∠5()又∵∠1=∠(对顶角相等)∴∠4=∠5（等量代换）两直线平行，同位角相等4活动2：运用与推理（1）如图，如果直线a∥b,那么∠4与∠5相等吗？请说明理由。性质2:两条平行直线被第三条直线所截,内错角相等。简称：两直线平行,内错角相等. 活动3：运用与推理（2）如图，如果直线a∥b,那么∠3与∠5的大小有什么关系呢？请说明理由。性质3:两条平行直线被第三条直线所截,同旁内角互补。简称：两直线平行,同旁内角互补.解：∵a∥b∴∠1=∠5∵∠1+∠3=1800∴∠3+∠5=1800 (第2题）C学以致用：cab12(第1题）1.如图，已知直线a,b被直线c所截，若a//b，∠1=120°，则∠2等于（）A、30°B、60°C、120°D、150°Cc2.如图，已知直线a,b被直线c所截，若a//b，∠1=60°，则∠2等于（）A、30°B、60°C、120°D、150°12ab60° 3.20°20° 4、如图所示，点B,C,D在同一条直线上，CE∥AB,∠ACB=90°，如果∠ECD=36°，那么∠A=54°ABCED36°？ 5.如图，已知直线a∥b，直线c∥d，∠1=110°,求∠2,∠3的度数。解：∵a∥b(已知)∴∠=∠1()∵∠1=110°()∴∠2=°∵c∥d()∴∠3=∠=°()两直线平行，内错角相等2已知2110已知110两直线平行，同位角相等请补充完整小明的做法：dcab123 6．如图，一束平行光线AB与DE射向一个水平镜面后被反射，此时∠1=∠2，∠3=∠4．（1）∠1与∠3的大小有什么关系？∠2与∠4呢？（2）反射光线BC与EF也平行吗？解：解：（1）∵AB∥DE（已知）∴∠1=∠3（）∵∠1=∠2（已知）∠3=∠4（已知）∴∠2=∠4（）两直线平行，同位角相等等量代换（2）由（1）知∠2=∠4∴BC∥EF()同位角相等，两直线平行 联系拓广，综合应用1．如图，已知D是AB上的一点，E是AC上的一点，∠ADE=60°，∠B=60°，∠AED=40°。（1）DE和BC平行吗？为什么？（2）∠C是多少度？为什么？ 2.如图，AE∥BC,∠B=∠C,试说明∠1=∠2.DAEBC12 1、平行线的3条性质：两直线平行同旁内角互补内错角相等同位角相等3、平行线的性质与判定的区别。通过这节课的学习你有什么收获？2、平行线的性质的应用。课堂小结： 课本第51页习题2.5第1、2题。布置作业：