七年级下册数学课件《探索三角形全等的条件 边边边判定》 (5)_北师大版 26页

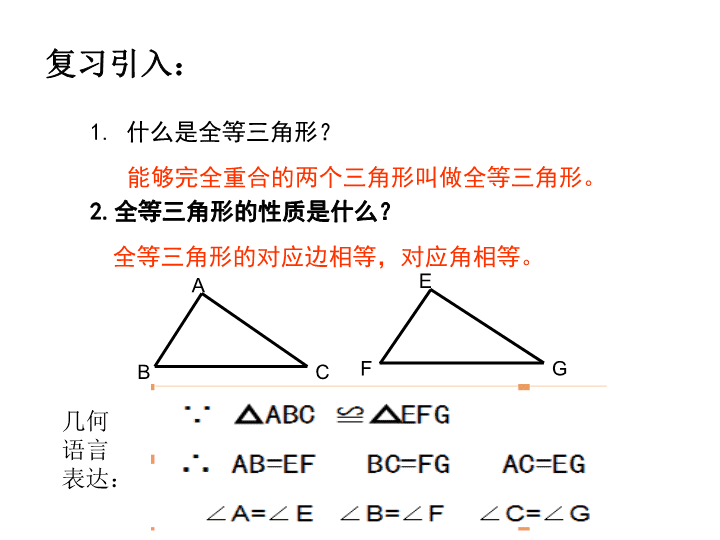
1.什么是全等三角形？2.全等三角形的性质是什么？EFGABC全等三角形的对应边相等，对应角相等。能够完全重合的两个三角形叫做全等三角形。复习引入：几何语言表达： 本节课的学习目标：1、经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程。2、了解三角形的稳定性。3、掌握三角形全等的判断条件，并掌握其几何书写格式。4、在三角形全等应用过程中，能够进行有条理地思考并进行简单推理。 想一想：要画一个三角形与小明画的三角形全等，需要几个与边或角的大小有关的条件呢？现在我们就来一起探究。 探究活动一：1.都给边：给一条边2.都给角：给一个角给一个条件 有一条边对应相等的三角形不一定全等有一个角对应相等的三角形不一定全等举反例： 探究活动二：给两个条件1.都给边：给两条边2.都给角：给两个角给一条边，一个角3.既给角，又给边： 三角形的两条边分别为4cm，6cm.4cm6cm4cm不一定全等1、给出两条边举反例： 三角形的两个内角分别为30°和50°；50o50o30o不一定全等2、给出两个角 三角形的一个内角为30°，一条边为3cm；30o3cm不一定全等3、给出一个角一条边 探究活动三：给三个条件2.都给边：给三条边1.都给角：给三个角3.给两边一角：给两条边，一个角4.给两角一边：给两个角，一条边今天我们先来探究前两个 三角形的三个内角分别为30°、60°、90°；60o60°30o不一定全等1、给出三个角90°90° 2、给出三条边：四人为一个小组合作完成。已知三角形三条边分别是4cm，5cm，7cm，画出这个三角形，把所画的三角形分别剪下来，并与同伴比一比，发现什么？结论：三条边分别相等的两个三角形全等。 有三边对应相等的两个三角形全等.可以简写成“边边边”或“SSS”ABCDEF用几何语言表示：在△ABC和△DEF中∴△ABC△DEF（SSS）AB=DEBC=EFCA=FD三角形全等条件：≌ 总结三角形全等书写步骤：①写出在哪两个三角形中②摆出三个条件用大括号括起来③写出全等结论 做一做（1）取出三根木条钉成一个三角形，你能拉动其中两边，使这个三角形的形状发生变化吗？（形状没有发生改变）（2）取出四根木条钉成一个四边形，拉动其中两边，这个四边形的形状改变了吗？钉成一个五边形，六边形等又会怎么样？（形状发生改变）（3）上面的现象说明了什么？三角形具有稳定性 你能找到图中的三角形吗？你能说出为什么这些地方是三角形吗? 例1:如图，AB=CD，AC=BD，△ABC和△DCB是否全等？试说明理由。BCDA(SSS)在△ABC和△DBC中AB=DC（已知）BC=CB（公共边）AC=DB（已知）∴△ABC≌△DCB解：新知应用△ABC≌△DCB理由如下： 针对练习：如图，在四边形ABCD中，AB=AD,BC=DC.试说明：∠B=∠DDABC 例2：如图，已知:AE=BF,CE=DF,AB=CD求证：AE∥BFABCDFE 针对练习：已知：如图所示，E,F在BC上，BE=CF,AB=DC,AF=DE,说明：∠B=∠CABEFCD 课堂小结：本节课你收获了什么？1、学会用分类思想探究三角形全等。2、理解三角形全等的判断条件“边边边”定理。3、学会用几何语言有条理地书写三角形全等，并进行简单的综合证明。 闯关练习：1、如图，点B,C,D,E在同一条直线上，且BC=DE,AC=FD,AE=FB求证：AE∥BFAEDCBF 2、如图，AE=CF,AD=BC,DF=BE.求证：AD∥BCADFEBC 工人师傅常用角尺平分一个任意角。做法如下：如图：∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线。为什么？挑战自我(SSS)在△OMC和△ONC中CM=CN（已知）OC=OC（公共边）OM=ON（已知）∴△OMC≌△ONC∴∠MOC=∠NOC∴OC便是∠AOB的平分线解： 作业布置：1、理解记忆今天所学的知识点。2、《课堂精炼》74页1-10题。