七年级数学下册知识点总汇 2页

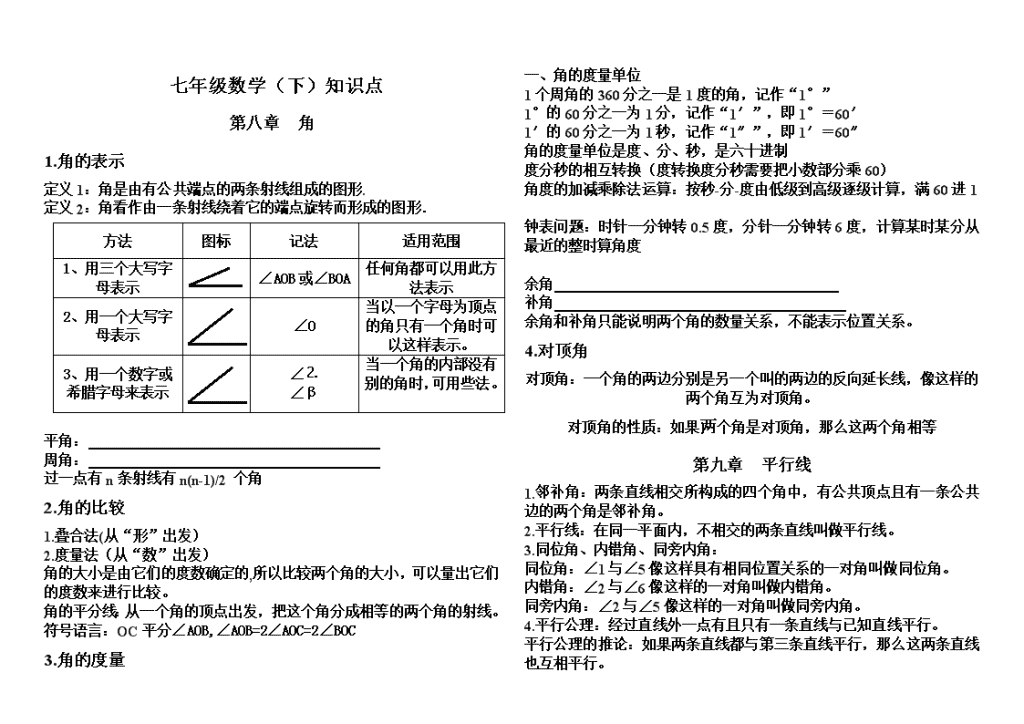
七年级数学（下）知识点 第八章 角 1.角的表示 定义 1：角是由有公共端点的两条射线组成的图形. 定义 2：角看作由一条射线绕着它的端点旋转而形成的图形． 平角： 周角： 过一点有 n条射线有 n(n-1)/2个角 2.角的比较 1.叠合法(从“形”出发） 2.度量法（从“数”出发） 角的大小是由它们的度数确定的,所以比较两个角的大小，可以量出它们 的度数来进行比较。 角的平分线：从一个角的顶点出发，把这个角分成相等的两个角的射线。 符号语言：OC平分∠AOB,∠AOB=2∠AOC=2∠BOC 3.角的度量 一、角的度量单位 1个周角的 360分之一是 1度的角，记作“1°” 1°的 60分之一为 1分，记作“1′”，即 1°＝60′ 1′的 60分之一为 1秒，记作“1″”，即 1′＝60″ 角的度量单位是度、分、秒，是六十进制 度分秒的相互转换（度转换度分秒需要把小数部分乘 60） 角度的加减乘除法运算：按秒-分-度由低级到高级逐级计算，满 60进 1 钟表问题：时针一分钟转 0.5 度，分针一分钟转 6度，计算某时某分从 最近的整时算角度 余角 补角 余角和补角只能说明两个角的数量关系，不能表示位置关系。 4.对顶角 对顶角：一个角的两边分别是另一个叫的两边的反向延长线，像这样的 两个角互为对顶角。 对顶角的性质：如果两个角是对顶角，那么这两个角相等 第九章 平行线 1.邻补角：两条直线相交所构成的四个角中，有公共顶点且有一条公共 边的两个角是邻补角。 2.平行线：在同一平面内，不相交的两条直线叫做平行线。 3.同位角、内错角、同旁内角： 同位角：∠1与∠5像这样具有相同位置关系的一对角叫做同位角。 内错角：∠2与∠6像这样的一对角叫做内错角。 同旁内角：∠2与∠5像这样的一对角叫做同旁内角。 4.平行公理：经过直线外一点有且只有一条直线与已知直线平行。 平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线 也互相平行。 方法 图标 记法 适用范围 1、用三个大写字 母表示 ∠AOB 或∠BOA 任何角都可以用此方 法表示 2、用一个大写字 母表示 ∠O 当以一个字母为顶点 的角只有一个角时可 以这样表示。 3、用一个数字或 希腊字母来表示 ∠⒉ ∠β 当一个角的内部没有 别的角时，可用些法。 5.平行线的性质：性质 1：两直线平行，同位角相等。 性质 2：两直线平行，内错角相等。 性质 3：两直线平行，同旁内角互补。 6.平行线的判定： 判定 1：同位角相等，两直线平行。 判定 2：内错角相等，两直线平行。 判定 3：同旁内角相等，两直线平行。 第十章 二元一次方程组 1.二元一次方程：含有两个未知数，并且未知数 的指数都是 1，像这样的方程叫做二元一次。方程，一般形式是 ax+by=c(a≠0,b≠0)。 2.二元一次方程组：把两个二元一次方程合在一起，就组成了一个二元 一次方程组。 3.二元一次方程的解：一般地，使二元一次方程两边的值相等的未知数 的值叫做二元一次方程组的解。 4.二元一次方程组的解：一般地，二元一次方程组的两个方程的公共解 叫做二元一次方程组。 5.消元：将未知数的个数由多化少，逐一解决的想法，叫做消元思想。 6.代入消元：将一个未知数用含有另一个未知数的式子表示出来，再代 入另一个方程，实现消元，进而求得这个二元一次方程组的解，这种方 法叫做代入消元法，简称代入法。 7.加减消元法：当两个方程中同一未知数的系数相反或相等时，将两个 方程的两边分别相加或相减，就能消去这个未知数，这种方法叫做加减 消元法，简称加减法。 第十一章 整式的乘除 1.同底数幂的乘法法则: nmnm aaa  (m,n 都是正数) 2.. 幂的乘方法则：    mnnmnm aaa   (m,n 都是正数) 3.积的乘方法则  mmm baab    是正整数是常数，其中 mncMncb cmacM cnbmMa       ).( ),( )(, 为奇数时当 为偶数时当 一般地 na na a n n n 3. 整式的乘法 （1） 单项式乘法法则:单项式相乘,把它们的系数、相同字母分别相乘， 对于只在一个单项式里含有的字母，连同它的指数作为积的一个因式。 （2）单项式与多项式相乘:单项式乘以多项式，是通过乘法对加法的分 配律，把它转化为单项式乘以单项式，即单项式与多项式相乘，就是用 单项式去乘多项式的每一项，再把所得的积相加。 （3）．多项式与多项式相乘 多项式与多项式相乘，先用一个多项式中的每一项乘以另一个多项式的 每一项，再把所得的积相加。 4．平方差公式: 22))(( bababa  5．完全平方公式: 222 2)( bababa 